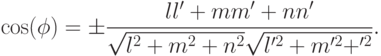НОУ ИНТУИТ | Введение в Octave. Лекция 6: Векторная алгебра и аналитическая геометрия

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Пример 6.21. Найти направляющие коэффициенты прямой 2x - 2y - z + 8 = 0 и x + 2y - 2z + 1 = 0 (листинг 6.24).

	
N1=[2, -2, -1];N2= [ 1, 2, -2 ];
% Расчёт координат векторного произведения		
M=[N1; N2 ];
M1=M( 1 : 2, 2 : 3 );M2=[M( :, 1 ),M( :, 3 ) ]; M3=M( 1 : 2, 1 : 2 );
a ( 1 )=det (M1); a ( 2 )= _det (M2); a ( 3 ) =( det (M3) );
a
% Векторное произведение
a = 6  3  6

Листинг 6.22. Расчёт направляющих коэффициентов прямой (пример 6.21).

Рис. 6.17. Геометрическая интерпретация примера 6.20, случай a)

Рис. 6.18. Геометрическая интерпретация примера 6.20, случай b)

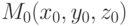Прямая , проходящая через точку M_0(x_0,y_0,z_0) и имеющая направляющий вектор 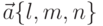$\vec{a}\{l,m,n\}$ представляется уравнениями 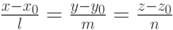$\frac{x-x_{0}}{l}=\frac{y-y_{0}}{m}=\frac{z-z_{0}}{n}$ . Эти уравнения выражают коллинеарность векторов 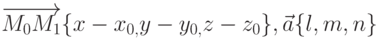$\overrightarrow{{M_{0}M_{1}}}\{x-x_{0,}y-y_{0,}z-z_{0}\},\vec{a}\{l,m,n\}$ и называются каноническими уравнениями прямой.

Уравнения 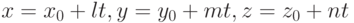x = x_0 + lt, y = y_0 + mt, z = z_0 + nt называют параметрическими уравнениями прямой. Здесь величина является параметром и принимает различные значения.

Пример 6.22. Записать параметрическое уравнение прямой, проходящей через две точки A(5, -3, 2) и B(3, 1, -2) .

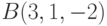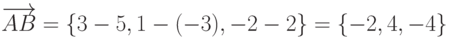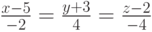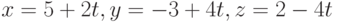Если в качестве направляющего вектора выбрать вектор $\overrightarrow{AB}=\{3-5,1-(-3),-2-2\}=\{-2,4,-4\}$ , то каноническое уравнение будет иметь вид $\frac{x-5}{-2}=\frac{y+3}{4}=\frac{z-2}{-4}$ , следовательно параметрическое уравнение запишем так x = 5 + 2t, y = -3 + 4t, z = 2 - 4t .

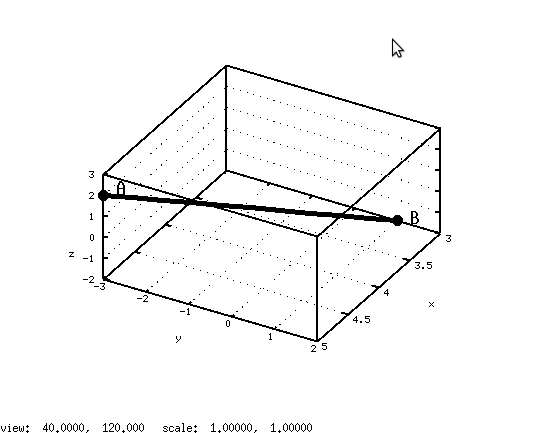
Команды, которые применялись для графического решения примера (рис. 6.19) показаны в листинге 6.23.

	
clf; cla;
set( gcf, ’Position’, [ 20, 20, 400, 400 ] );
set( gca, ’Position’, [ . 1, . 1, . 8, . 8 ] );
xlabel( ’x’ ); ylabel ( ’y’ ); zlabel ( ’z’ );
axis( [ 3, 5, - 3, 2, -2, 3 ] );
grid on;
% Исходные данные
A= [ 5, - 3, 2 ];B= [ 3, 1, - 2 ];
t = 0 : 0.1 : 1;
x=5-2* t; y= -3+4* t; z=2-4* t;
% Изображение прямой
line( x, y, z, ’LineWidth’, 5, ’Color’, ’k’ );
% Изображение точек
line( [A( 1 ),A( 1 ) ], [ A( 2 ),A( 2 ) ], [ A( 3 ),A( 3 ) ], ’LineWidth’, 5, ’Color’
	, ’k’, ’marker’, ’o’, ’markersize’, 1 0 );
line ( [ B( 1 ),B( 1 ) ], [ B( 2 ),B( 2 ) ], [ B( 3 ),B( 3 ) ], ’LineWidth’, 5, ’Color’
	, ’k’, ’marker’, ’o’, ’markersize’, 1 0 );		
% Подписи
text(A( 1 ),A( 2 ) +0.3,A( 3 ) +0.5, ’A’, ’FontSize’, 20 );
text(B( 1 ),B( 2 ) +0.3,B( 3 ) +0.3, ’B’, ’FontSize’, 20 );
set( gca, ’View’, [ 120 50 ] );

Листинг 6.23. Построение прямой по параметрическим уравнениям (пример 6.22).

Рис. 6.19. Прямая, проходящая через две точки

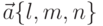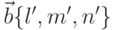Если известны направляющие векторы двух прямых $\vec{a}\{l,m,n\}$ и $\vec{b}\{l',m',n'\}$ , то угол между этими прямыми можно вычислить по формуле

$\cos (\phi )=\pm {\frac{ll'+mm'+nn'}{\sqrt{l^{2}+m^{2}+n^{2}}\sqrt{l'^{2}+m'^{2}+'^{2}}}}.$

Дальше >>

Авторизоваться

Введение в Octave

Векторная алгебра и аналитическая геометрия

Вопросы и ответы