|
Возможна ли разработка приложения на Octave с GUI? |
Компания ALT Linux
Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 585 / 65 | Длительность: 20:55:00
Темы: Математика, Программное обеспечение, Физика
Специальности: Математик, Преподаватель, Физик
Лекция 6:
Векторная алгебра и аналитическая геометрия
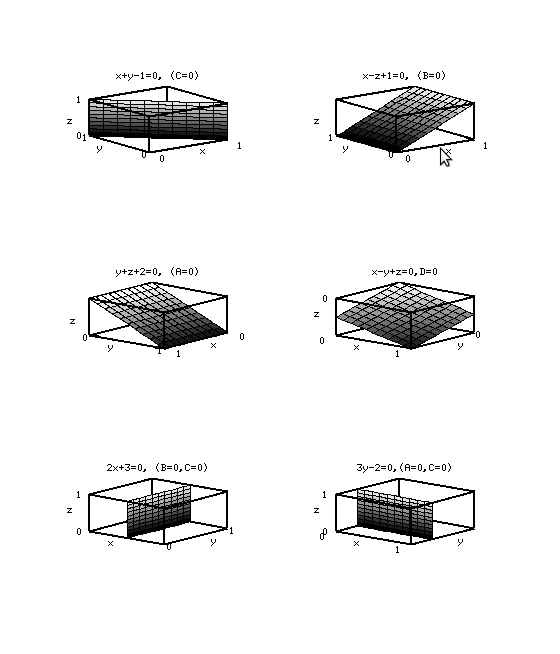
Пример 6.17. Построить плоскости 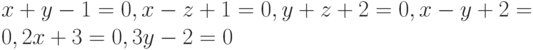 .
.
Ход решения примера описан в листинге 6.18. Графическое решение показано на рис. 6.16.
function p=plos1 (A, B, C,D) M=[A, B,C ]; % Параметры плоскости d = [ 0.1, 0.1, 0.1 ]; if A==0 M( 1 ) =1; end; if B==0 M( 2 ) =1; end; if C==0 M( 3 ) =1; end; if A<0 d ( 1 ) = -0.1; end; if B<0 d ( 2 ) = -0.1; end; if C<0 d ( 3 ) = -0.1; end; X=0:d ( 1 ) :M( 1 ); Y=0:d ( 2 ) :M( 2 ); Z=0:d ( 3 ) :M( 3 ); % Построение плоскости if C!=0 % Плоскость не параллельна OZ % Уравнение плоскости преобразовано к функции двух переменных z(x,y) [ x, y]= meshgrid(X,Y); b0= - D/C; b1= - A/C; b2= - B/C; z=b0+b1 _ x+b2 _ y; f1=surf ( x, y, z ); colormap gray else if B!=0 % Плоскость не параллельна OY % Уравнение плоскости преобразовано к функции двух переменных y(x,z) [ x, z ]= meshgrid(X, Z); b0= - D/B; b1= - A/B; b2= - C/B; y=b0+b1 * x+b2 * z; f1=surf ( x, y, z ); colormap gray else % Плоскость не параллельна OX % Уравнение плоскости преобразовано к функции двух переменных x(y,z) [ y, z ]= meshgrid(Y, Z); b0= - D/A; b1= - B/A; b2= - C/A; x=b0+b1 * y+b2 * z; f1=surf( x, y, z ); colormap gray end; end; grid on; xlabel ( ’x’ ); ylabel ( ’y’ ); zlabel ( ’z’ ); set( gca, ’xtick’, [ 0 :M( 1 ) ] ); set( gca, ’ytick’, [ 0 :M( 2 ) ] ); set( gca, ’ztick’, [ 0 :M( 3 ) ] ); set( gca, ’box’, ’on’ ); p=f1; end; % конец функции % Изображение плоскостей заданных в примере 6.17 clf; cla; subplot ( 3, 2, 1 ); A1=1;B1=1;C1=0;D1=-1; % Плоскость x+y-1=0 plos1 (A1, B1, C1, D1); title ( ’x+y-1=0, (C=0)’ ); subplot ( 3, 2, 2 ); A2=1;B2=0;C2=_1;D2=1; % Плоскость x-z+1=0 plos1 (A2, B2, C2, D2); title ( ’x-z+1=0, (B=0)’ ); subplot ( 3, 2, 3 ); A3=0;B3=1;C3=1;D3=2; % Плоскость y+z+2=0 plos1 (A3, B3, C3, D3); title ( ’y+z+2=0, (A=0)’ ); set ( gca, ’View’, [ 1 3 0 3 0 ] ); subplot ( 3, 2, 4 ); A4=1;B4=-1;C4=1;D4=0; % Плоскость x-y+z-2=0 plos1 (A4, B4, C4, D4); set ( gca, ’View’, [ 4 0 3 0 ] ); title ( ’x-y+z=0,D=0’ ); subplot ( 3, 2, 5 ); A5=2;B5=0;C5=0;D5=3; % Плоскость 2x+3=0 plos1 (A5, B5, C5, D5); set ( gca, ’View’, [ 4 0 3 0 ] ); title ( ’2x+3=0, (B=0,C=0)’ ) subplot ( 3, 2, 6 ); A6=0;B6=3;C6=0;D6=_2; % Плоскость 3y-2=0 plos1 (A6, B6, C6, D6); set ( gca, ’View’, [ 4 0 3 0 ] ); title ( ’3y-2=0,(A=0,C=0)’ );Листинг 6.18. Построение нескольких плоскостей (пример 6.17).
Расстояние от точки 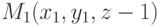 до плоскости
до плоскости 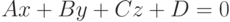 равно абсолютному значению величины
равно абсолютному значению величины
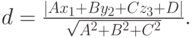
Пример 6.18. Найти расстояние от точки M1 (3, 9, 1) до плоскости 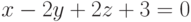 .
.
Решение показано в листинге 6.19.
% Исходные данные A=1;B=-2;C=2;D=-3;M= [ 3, 9, 1 ];N=[A;B;C ]; % Расстояние от точки М(3,9,1) до плоскости x-2y+2z-3=0 d=abs (M *N+D) /norm(N) d = 5.3333Листинг 6.19. Вычисление расстояния от точки до плоскости.
Две плоскости 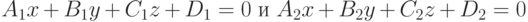 образуют четыре двугранных угла равных попарно. Один из них всегда равен углу между нормальными векторами
образуют четыре двугранных угла равных попарно. Один из них всегда равен углу между нормальными векторами 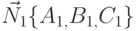 . Вычисляют любой из двугранных углов по формуле
. Вычисляют любой из двугранных углов по формуле
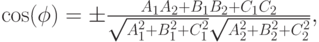
причём, выбирая "+" получаем  , выбирая "–" получаем
, выбирая "–" получаем 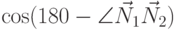 .
.