|
Возможна ли разработка приложения на Octave с GUI? |
Векторная алгебра и аналитическая геометрия
Пример 6.10. Проверить, являются ли векторы  и
и 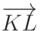 ,
,  и
и  взаимно перпендикулярными. Координаты точек:
взаимно перпендикулярными. Координаты точек: 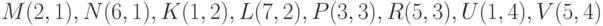 .
.
Если 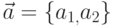 и
и 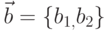 , то их скалярное произведение равно нулю:
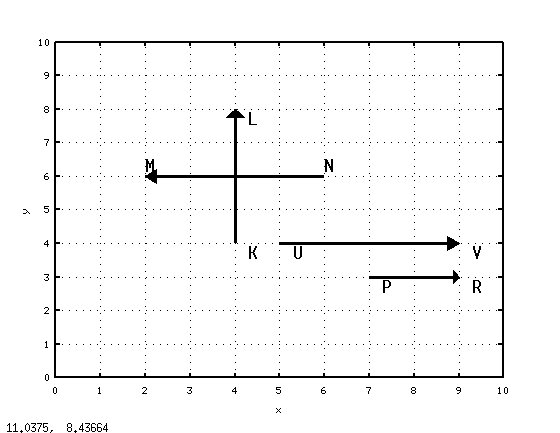
, то их скалярное произведение равно нулю: 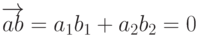 . На рис. 6.8 видно, что векторы
. На рис. 6.8 видно, что векторы  и
и 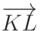 перпендикулярны, а
перпендикулярны, а  и
и  нет. Аналитические вычисления подтверждают это (листинг 6.10).
нет. Аналитические вычисления подтверждают это (листинг 6.10).
% Вычисление скалярного произведения векторов a и b function[ab]= scal(a, b) ab=a(1)*b(1)+a(2)*b(2); end; clf; cla; set(gcf, ’Position’, [20, 20, 400, 400]); set(gcf, ’numbertitle’, ’off’) set(gcf, ’name’, ’Vector’) set(gca, ’Position’, [.1, .1, .8, .8]); set(gca, ’xlim’, [0, 10]); set(gca, ’ylim’, [0, 10]); set(gca, ’xtick’, [0 : 10]); set(gca, ’ytick’, [0 : 10]); grid on; xlabel(’x’); ylabel(’y’); M= [2, 6];N= [6, 6];K= [4, 4]; L = [4, 8]; P= [7, 3];R= [9, 3];U= [5, 4];V= [9, 4]; MN_KL=scal(N-M, L-K) PR_UV=scal(R-P, V-U) vector(N,M); % Построение вектора NM N_=text(N(1),N(2)+0.3, ’N’); set(N_, ’FontSize’, 20) M_=text(M(1),M(2)+0.3, ’M’); set(M_, ’FontSize’, 20) vector(K,L); % Построение вектора KL K_=text(K(1)+0.3,K(2)-0.3, ’K’); set(K_, ’FontSize’, 20) L_=text(L(1)+0.3,L(2)-0.3, ’L’); set(L_, ’FontSize’, 20) % Построение вектора PR vector(P,R); % Построение вектора PR P_=text(P(1)+0.3,P(2)-0.3, ’P’); set(P_, ’FontSize’, 20) R_=text(R(1)+0.3,R(2)-0.3, ’R’); set(R_, ’FontSize’, 20) vector(U,V);% Построение вектора UV U_=text(U(1)+0.3,U(2)-0.3, ’U’); set(U_, ’FontSize’, 20) V_=text(V(1)+0.3,V(2)-0.3, ’V’); set(V_, ’FontSize’, 20) % Результат работы программы MN_KL = 0 PR_UV = 8Листинг 6.10. Проверка перпендикулярности векторов (пример 6.10).
Векторным произведением вектора 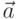 на не коллинеарный с ним вектор
на не коллинеарный с ним вектор 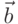 называется вектор
называется вектор 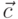 , модуль которого численно равен площади параллелограмма построенного на векторах
, модуль которого численно равен площади параллелограмма построенного на векторах  и
и 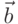 :
: 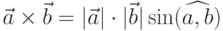 . Направление вектора
. Направление вектора  перпендикулярно плоскости параллелограмма. Если векторы
перпендикулярно плоскости параллелограмма. Если векторы 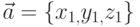 и
и 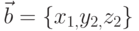 , то
, то  .
.
Пример 6.11. Найти векторное произведение векторов 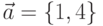 и
и 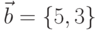 . Вычислить угол между векторами.
. Вычислить угол между векторами.
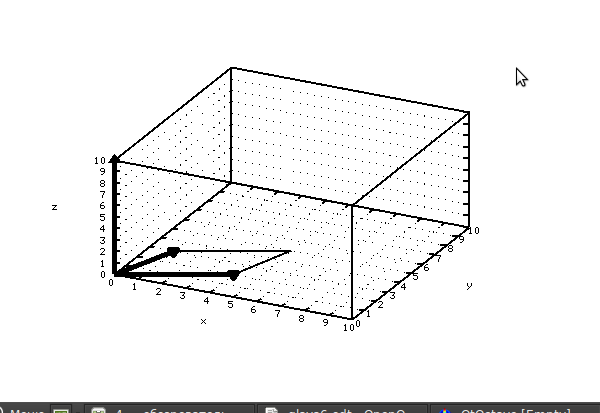
Графическое решение показано на рис. 6.9. Листинг 6.11 содержит текст программы и результаты её работы.
clear all; clf; cla; set(gcf, ’Position’, [20, 20, 400, 400]); set(gcf, ’numbertitle’, ’off’) set(gcf, ’name’, ’Vector’) set(gca, ’Position’, [.1, .1, .8, .8]); set(gca, ’xlim’, [0, 10]); set(gca, ’ylim’, [0, 10]); set(gca, ’zlim’, [0, 10]); set(gca, ’xtick’, [0 : 10]); set(gca, ’ytick’, [0 : 10]); set(gca, ’ztick’, [0 : 10]); set(gca, ’View’, [30 30], ’box’, ’on’); xlabel(’x’); ylabel(’y’); zlabel(’z’); axis([0, 10, 0, 10, 0, 10]); grid on; function D=dlin(x) % Длина вектора D=(x(1)^2+x(2)^2+x(3)^2)^(1/2); end; function gr=rad_gr(rad) % Перевод радиан в градусы и минуты gr(1)= round(rad*180/pi); % Градусы gr(2)= round((rad*180/pi_gr(1))*60); % Минуты end; % Исходные данные x1 =4; y1 =2; z1 =0; x2 =1; y2 =3; z2 =0; a=[x1, y1, z1]; b=[x2, y2, z2]; % Расчёт координат векторного произведения M=[a; b]; M1=M(1:2, 2:3);M2=[M(:, 1),M(:, 3)]; M3=M(1:2, 1:2); c(1)=det(M1); c(2)=-det(M2); c(3)=(det(M3)); % Расчёт угла между векторами a и b da=dlin(a); db=dlin(b); dc=dlin(c); alf=asin(dc/(da*db)); % Изображение векторов a,b,c line([0, a(1)], [0, a(2)], [0, a(3)], ’LineWidth’, 5, ’Color’, ’k’); line([0, b(1)], [0, b(2)], [0, b(3)], ’LineWidth’, 5, ’Color’, ’k’); line([0, c(1)], [0, c(2)], [0, c(3)], ’LineWidth’, 5, ’Color’, ’k’); % Изображение стрелок на векторах line([c(1), c(1)], [c(2), c(2)], [c(3), c(3)], ’LineWidth’, 5, ’Color’ , ’k’, ’marker’, ’^’, ’markersize’, 16); line([b(1), b(1)], [b(2), b(2)], [b(3), b(3)], ’LineWidth’, 5, ’Color’ , ’k’, ’marker’, ’<’, ’markersize’, 10); line([a(1), a(1)], [a(2), a(2)], [a(3), a(3)], ’LineWidth’, 5, ’Color’ , ’k’, ’marker’, ’<’, ’markersize’, 10); % Расчёт координат вершины параллелограмма k1=y1/x1; k2=y2/x2; d(1) =(y1-y2+k1*x2-k2*x1)/(k1-k2); d(2)=k1*d(1)+y2-k1*x2; d(3) =0; % Стороны параллелограмма line([a(1),d(1)],[a(2),d(2)],[a(3),d(3)], ’LineWidth’, 2, ’Color’, ’k’); line([b(1),d(1)],[b(2),d(2)],[b(3),d(3)], ’LineWidth’, 2, ’Color’, ’k’); c % Координаты векторного произведения alfa=rad_gr(alf) % Угол между векторами a и b % Результаты работы программы — координаты векторного произведения c = 0 -0 10 % Угол между векторами alfa = 45 -0Листинг 6.11. Векторное произведение векторов (пример 6.11).
Три вектора называют компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости. Смешанным или векторно-скалярным произведением трёх векторов 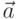 ,
,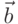 и
и 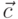 называется скалярное произведение вектора
называется скалярное произведение вектора 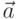 на векторное произведение
на векторное произведение  , то есть число
, то есть число 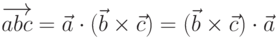 . Если векторы
. Если векторы 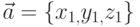 ,
, 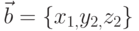 и
и 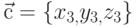 даны своими координатами, то смешанное произведение вычисляют по формуле:
даны своими координатами, то смешанное произведение вычисляют по формуле:
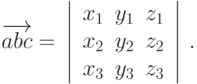
Необходимым и достаточным условием компланарности векторов 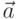 ,
, 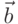 и
и 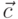 является равенство нулю их смешанного произведения
является равенство нулю их смешанного произведения 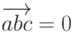 .
.
Пример 6.12. Проверить компланарность векторов (листинг 6.12):
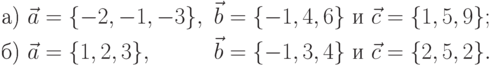
function d=komp(A, B,C) M=[A;B;C ]; d=det (M); if d==0 disp(’Векторы компланарны’); else disp(’Векторы не компланарны’); end; end; a =[-2, -1, -3];b = [-1, 4, 6]; c = [1, 5, 9]; d1=komp(a, b, c) a = [ 1, 2, 3 ]; b = [ -1, 3, 4 ]; c = [ 2, 5, 2 ]; d2=komp( a, b, c ) % Результат работы программы Векторы компланарны d1 = 0 Векторы не компланарны d2 = -27Листинг 6.12. Поверка компланарности векторов (пример 6.12).