НОУ ИНТУИТ | Введение в Octave. Лекция 12: Обработка результатов эксперимента. Интерполяция функций

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Данная лекция посвящена решению часто встречающихся на практике задач по обработке реальных количественных экспериментальных данных, полученных в результате всевозможных научных опытов, технических испытаний методом интерполяции. Описаны численные методы интерполирования, а также рассмотрено решение задач интерполирования в Octave.

12.1 Постановка задачи

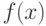Напомним читателю задачу интерполирования. На отрезке [a, b] заданы n + 1 точка x_0,x_1,x_2,...,x_n(a=x_0,b=x_n) , называемые узлами интерполяции, и значения неизвестной функции f (x) в этих точках

f(x_0)=y_0,f(x_1)=y_1,f(x_2)=y_2,...,f(x_n)=y_n

( 12.1)

Требуется построить интерполирующую функцию F (x) , которая в узлах интерполяции принимает те же значения, что и f (x)

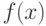
( 12.2)

В общей постановке задача может не иметь однозначного решений или совсем не иметь решений. Задача становится однозначной, если функцию F (x) будем искать в виде полинома F(x)=P_n(x) степени , удовлетворяющий условиям (12.2).

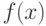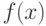Полученную интерполяционную формулу y = F (x) зачастую используют для приближённого нахождения значений данной функции f (x) в точках , отличных от узлов интерполирования. Такая операция называется интерполированием функции f (x) . При этом различают интерполирование в узком смысле, когда $x\in[x_0,x_n]$ , и экстраполирование, когда $x\notin[x_0,x_n]$ .

Рассмотрим некоторые наиболее часто используемые интерполяционные полиномы.

12.1.1 Канонический полином

Будем искать интерполирующую функцию F (x) в виде канонического полинома степени .

$F(x)=P_n(x)=a_0+a_1x+a_2x^2+\cdot\cdot\cdot+a_nx^n$

( 12.3)

Выбор многочлена степени основан на том факте, что через n + 1 точку проходит единственная кривая степени . Подставив (12.3) в (12.1), получим систему линейных алгебраических уравнений (12.4).

$\left\{\begin{aligned}a_0,a_1x_0+a_2x_0^2+\cdots+a_nx_0^n=y_0\\a_0,a_1x_1+a_2x_1^2+\cdots+a_nx_1^n=y_1\\a_0,a_1x_2+a_2x_2^2+\cdots+a_nx_2^n=y_2\\\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots\\a_0,a_1x_n+a_2x_n^2+\cdots+a_nx_n^n=y_n\end{aligned}$

( 12.4)

Решая эту систему линейных алгебраических уравнений, найдём коэффициенты интерполяционного полинома a_0,a_1,...,a_n .

Дальше >>

Авторизоваться

Введение в Octave

Обработка результатов эксперимента. Интерполяция функций

12.1 Постановка задачи

12.1.1 Канонический полином

Вопросы и ответы