|
Возможна ли разработка приложения на Octave с GUI? |
Векторная алгебра и аналитическая геометрия
Пример 6.4. Проверить коллинеарны ли векторы  и
и 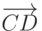 ,
, и
и 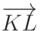 ,
,  и
и  . Координаты точек:
. Координаты точек: 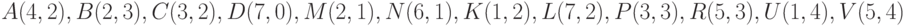 .
.
Текст файла-сценария представлен в листинге 6.4. При решении примера была создана функция 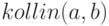 , которая определяет коллинеарны ли векторы
, которая определяет коллинеарны ли векторы 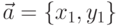 и
и 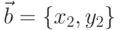 . Результатом работы функции является коэффициент пропорциональности векторов. Если векторы коллинеарны, то их соответствующие координаты пропорциональны:
. Результатом работы функции является коэффициент пропорциональности векторов. Если векторы коллинеарны, то их соответствующие координаты пропорциональны: 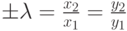 . Знак коэффициента пропорциональности говорит о направлении векторов: "+" — в одну сторону, "_" — в разные. Для изображения векторов использовалась функция
. Знак коэффициента пропорциональности говорит о направлении векторов: "+" — в одну сторону, "_" — в разные. Для изображения векторов использовалась функция 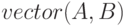 , описанная в листинге 6.2 к примеру 6.2.
, описанная в листинге 6.2 к примеру 6.2.
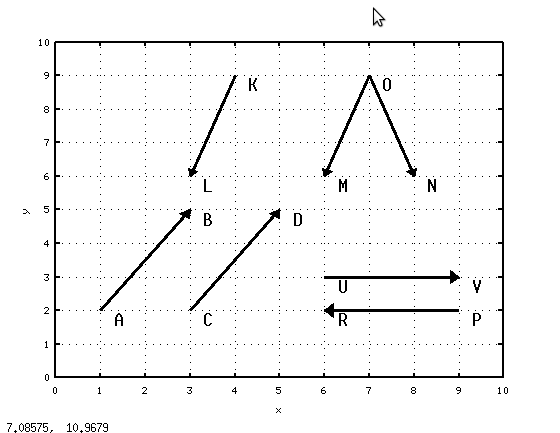
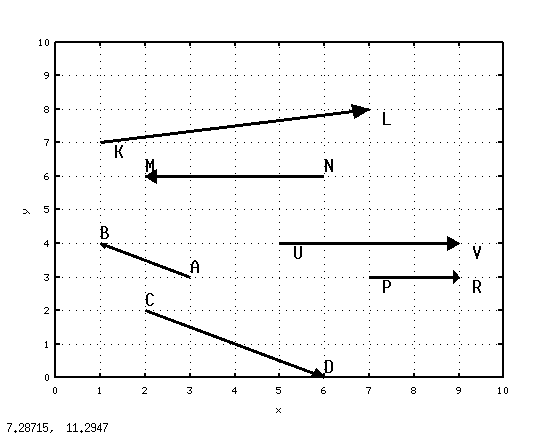
Решение примера показано в конце листинга 6.4 и на рис. 6.4. По полученным числовым результатам и геометрической интерпретации примера можно сделать вывод, что векторы  и
и 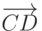 коллинеарны, но направлены в разные стороны. Векторы
коллинеарны, но направлены в разные стороны. Векторы  и
и 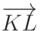 не являются коллинеарными. Векторы
не являются коллинеарными. Векторы  и
и  — коллинеарны и имеют одно направление.
— коллинеарны и имеют одно направление.
function[lam]= kollin(a, b) if (a(2)==0) & (b(2)==0) lam=a(1)/b(1); elseif (a(1)==0) & (b(1)==0) lam=a(2)/b(2); elseif a(1)/b(1)==a(2)/b(2) lam=a(1)/b(1); else lam=Inf; end; end; clf; cla; set(gcf, ’Position’, [20, 20, 400, 400]); set(gcf, ’numbertitle’, ’off’) set(gcf, ’name’, ’Vector’) set(gca, ’Position’, [.1, .1, .8, .8]); set(gca, ’xlim’, [0, 10]); set(gca, ’ylim’, [0, 10]); set(gca, ’xtick’, [0 : 10]); set(gca, ’ytick’, [0 : 10]); grid on; xlabel(’x’); ylabel(’y’); A= [3, 3];B= [1, 4];C= [2, 2];D= [6, 0];M= [2, 6];N= [6, 6]; K= [1, 7]; L= [7, 8];P= [7, 3];R= [9, 3];U= [5, 4];V= [9, 4]; AB_CD=kollin(B-A, D-C) MN_KL=kollin(N-M, L-K) PR_UV=kollin(R-P, V-U) vector(A,B);% Построение вектора AB A_=text(A(1),A(2)+0.3, ’A’); set(A_, ’FontSize’, 20) B_=text(B(1),B(2)+0.3, ’B’); set(B_, ’FontSize’, 20) vector(C,D); % Построение вектора CD C_=text(C(1),C(2)+0.3, ’C’); set(C_, ’FontSize’, 20) D_=text(D(1),D(2)+0.3, ’D’); set(D_, ’FontSize’, 20) vector(N,M); % Построение вектора NM N_=text(N(1),N(2)+0.3, ’N’); set(N_, ’FontSize’, 20) M_=text(M(1),M(2)+0.3, ’M’); set(M_, ’FontSize’, 20) vector(K, L); % Построение вектора KL K_=text(K(1)+0.3,K(2)-0.3, ’K’); set(K_, ’FontSize’, 20) L_=text(L(1)+0.3,L(2)-0.3, ’L’); set(L_, ’FontSize’, 20) vector(P,R); % Построение вектора PR P_=text(P(1)+0.3,P(2)-0.3, ’P’); set(P_, ’FontSize’, 20) R_=text(R(1)+0.3,R(2)-0.3, ’R’); set(R_, ’FontSize’, 20) vector(U,V); % Построение вектора UV U_=text(U(1)+0.3,U(2)-0.3, ’U’); set(U_, ’FontSize’, 20) V_=text(V(1)+0.3,V(2)-0.3, ’V’); set(V_, ’FontSize’, 20) % Результаты — коэффициенты пропорциональности векторов AB_CD = -0.50000 MN_KL = Inf PR_UV = 0.50000Листинг 6.4. Проверка коллинеарности векторов (пример 6.4).
Геометрической проекций вектора  на ось OX называется вектор
на ось OX называется вектор  , начало которого
, начало которого 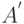 есть проекция точки
есть проекция точки  на ось OX, а конец
на ось OX, а конец 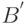 — проекция точки
— проекция точки  на ту же ось. Обозначается:
на ту же ось. Обозначается:
 . Алгебраической проекций вектора
. Алгебраической проекций вектора
 на ось OX называется длина вектора
на ось OX называется длина вектора  , взятая со знаком "+", если направление вектора
, взятая со знаком "+", если направление вектора  совпадает с направлением оси OX, или со знаком "-" в противном случае.
совпадает с направлением оси OX, или со знаком "-" в противном случае.
Пример 6.5. Найти проекции векторов  и
и  на ось OX. Координаты точек, задающих векторы:
на ось OX. Координаты точек, задающих векторы: 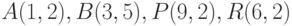 .
.
Текст файла-сценария и значения алгебраических проекций векторов представлены в листинге 6.5. При решении примера была создана функция 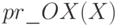 , которая вычисляет длину проекции вектора на ось OX. Аргументом функции является массив абсцисс
, которая вычисляет длину проекции вектора на ось OX. Аргументом функции является массив абсцисс 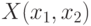 заданного вектора. Для изображения векторов и их проекций использовалась функция
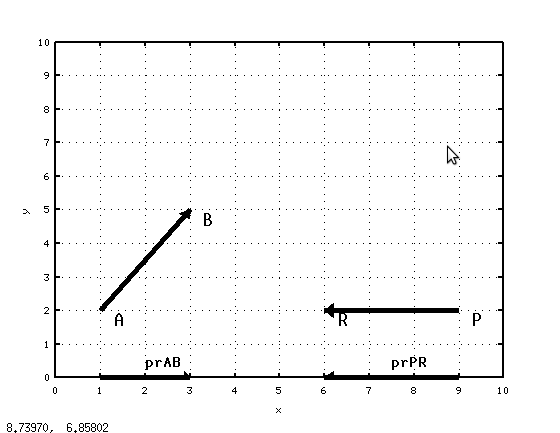
заданного вектора. Для изображения векторов и их проекций использовалась функция 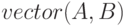 , описанная в примере 6.2. Геометрические проекции показаны на рис. 6.5.
, описанная в примере 6.2. Геометрические проекции показаны на рис. 6.5.
function pr=pr_OX(X) % Длина проекции вектора на ось ОХ pr=X(2)-X(1); end; clf; cla; set(gcf, ’Position’, [20, 20, 400, 400]); set(gcf, ’numbertitle’, ’off’) set(gcf, ’name’, ’Vector’) set(gca, ’Position’, [.1, .1, .8, .8]); set(gca, ’xlim’, [0, 10]); set(gca, ’ylim’, [0, 10]); set(gca, ’xtick’, [0 : 10]); set(gca, ’ytick’, [0 : 10]); grid on; xlabel(’x’); ylabel(’y’); A= [1, 2];B= [3, 5];P= [9, 2];R= [6, 2]; % Длины проекций prAB=pr_OX([A(1),B(1)]) prPR=pr_OX([P(1),R(1)]) vector(A,B);% Построение вектора AB A_=text(A(1)+0.3,A(2)-0.3, ’A’); set(A_, ’FontSize’, 20) B_=text(B(1)+0.3,B(2)-0.3, ’B’); set(B_, ’FontSize’, 20) % Построение проекции вектора АВ на ось ОХ mAB=vector([A(1), 0], [B(1), 0]); text(mAB(1),mAB(2)+0.5, ’prAB’, ’FontSize’, 18); vector(P,R); % Построение вектора PR P_=text(P(1)+0.3,P(2)-0.3, ’P’); set(P_, ’FontSize’, 20) R_=text(R(1)+0.3,R(2)-0.3, ’R’); set(R_, ’FontSize’, 20) % Построение проекции вектора PR на ось ОХ mPR=vector([P(1), 0], [R(1), 0]); text(mPR(1),mPR(2)+0.3, ’prPR’, ’FontSize’, 18); % Вычисление проекций prAB = 2 prPR = -3Листинг 6.5. Нахождение проекций векторов (пример 6.5).
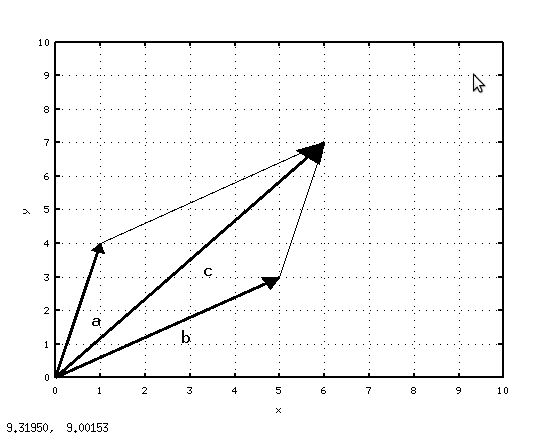
Любые векторы можно привести к общему началу, то есть построить векторы равные данным и имеющие общее начало в некоторой точке О.
Над векторами производят различные действия: сложение, вычитание, умножение.
При сложении\ (вычитании ) векторов их координаты складываются (вычитаются):  .
.
При умножении\ (делении ) вектора на число все координаты умножаются (делятся) на это число: 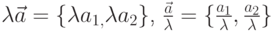 .
.