| Россия, Москва, МЭИ, 2006 |
Нейрофизиологический и формально-логический базис нейроподобных вычислений
В
табл. 4.4 даны численные значения 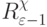 ,
,  и
и 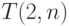 для
для 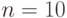 , что не было получено в [81] машинным способом.
, что не было получено в [81] машинным способом.
Все  -транспозиции, генерируемые оператором линейной свертки булевых векторов, можно получить, сняв ограничение (4.10) и выполнив над
-транспозиции, генерируемые оператором линейной свертки булевых векторов, можно получить, сняв ограничение (4.10) и выполнив над  группу переименований переменных [86]
группу переименований переменных [86] 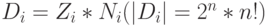 , которая представляет собой произведение группы перестановок
, которая представляет собой произведение группы перестановок 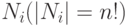 знакопеременной группы
знакопеременной группы  .
.
В этом случае (4.16) примет вид:
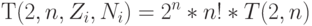 |
( 4.17) |
и при 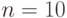
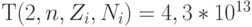 , что объясняет как вычислительные трудности прямого решения задач оптимального синтеза (М)ПМ за счет полной вариации весового вектора [79-81], так и стремление использовать модели формальных нейронов с непрерывными параметрами [87-89].
, что объясняет как вычислительные трудности прямого решения задач оптимального синтеза (М)ПМ за счет полной вариации весового вектора [79-81], так и стремление использовать модели формальных нейронов с непрерывными параметрами [87-89].
Обобщим комбинаторную схему (4.13), (4.15) на случай 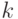 -значных входных векторов
-значных входных векторов 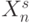 .
.
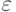 |
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 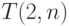 |
|---|---|---|---|---|---|---|---|---|---|
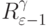 |
1 | 2 | 6 | 12 | 29 | 58 | 130 | 260 | 12222 |
 |
120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | |
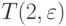 |
120 | 420 | 1512 | 2520 | 3480 | 2610 | 1300 | 260 | |
 |
84 | 126 | 126 | 84 | 36 | 9 | 1 | 3790 | |
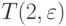 |
84 | 252 | 756 | 1002 | 1044 | 522 | 130 | ||
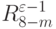 |
56 | 70 | 56 | 28 | 8 | 1 | 1158 | ||
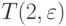 |
56 | 140 | 336 | 336 | 232 | 58 | |||
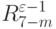 |
35 | 35 | 21 | 7 | 1 | 344 | |||
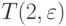 |
35 | 70 | 126 | 84 | 29 | ||||
 |
20 | 15 | 6 | 1 | 98 | ||||
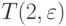 |
20 | 30 | 36 | 12 | |||||
 |
10 | 5 | 1 | 25 | |||||
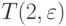 |
10 | 10 | 5 | ||||||
 |
4 | 1 | 6 | ||||||
 |
4 | 2 | |||||||
 |
1 | 1 | |||||||
 |
1 |
Если для булевых векторов отношение принадлежности 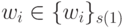
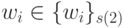 задается условием
задается условием 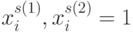 , то для
, то для 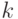 -значных входных векторов оно принимает вид
-значных входных векторов оно принимает вид 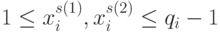 .
В результате каждая
.
В результате каждая  -транспозиция значений свертки булевых векторов порождает подкласс аддитивно-мультипликативных транспозиций (
-транспозиция значений свертки булевых векторов порождает подкласс аддитивно-мультипликативных транспозиций (  -транспозиций) вида:
-транспозиций) вида:
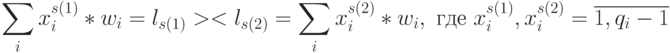
Например, при 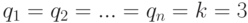
 -транспозиция
-транспозиция 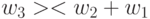 порождает
порождает  -транспозиции вида
-транспозиции вида 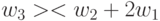 ,
, 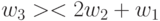 ,
, 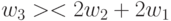 ,
, 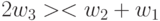 ,
, 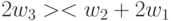 ,
,  причем первые три срабатывают при условии
причем первые три срабатывают при условии 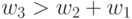 , а последние три - при условии
, а последние три - при условии 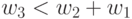 . Это объясняется тем, что любая комбинация
. Это объясняется тем, что любая комбинация  может инвертировать знак только одного из неравенств в порождающей
может инвертировать знак только одного из неравенств в порождающей  -транспозиции, а противоположное неравенство той же транспозиции она может только усилить.
-транспозиции, а противоположное неравенство той же транспозиции она может только усилить.
Выполнив в  -транспозиции
-транспозиции 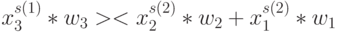 подстановки
подстановки 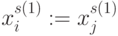 и
и 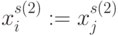 , отвечающие по
, отвечающие по 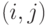 подстановкам
подстановкам 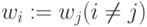 комбинаторной схемы (4.13), (4.15) можно получить все
комбинаторной схемы (4.13), (4.15) можно получить все  -транспозиции типа (
-транспозиции типа ( 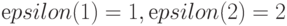 ).
).
Аналогично для  -транспозиций типа (
-транспозиций типа ( 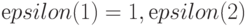 ), из которых остальные транспозиции схемы (4.13), (4.15) были получены перестановками компонент весового вектора вида
), из которых остальные транспозиции схемы (4.13), (4.15) были получены перестановками компонент весового вектора вида 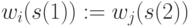 , что при
, что при 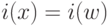 соответствует перестановкам
соответствует перестановкам  -значных компонент входного вектора вида
-значных компонент входного вектора вида 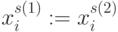 .
.
Чтобы определить количество порождаемых таким способом  -транспозиций, рассмотрим вектора
-транспозиций, рассмотрим вектора 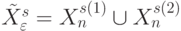 , которые представляют объединение неравных нулю
, которые представляют объединение неравных нулю  -значных компонент входных векторов
-значных компонент входных векторов 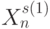 и
и 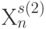 с взаимно исключающими индексами
с взаимно исключающими индексами 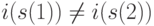 , где
, где  ,
,  ,
, 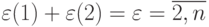 ,
, 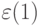 ,
, 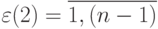 , а
, а  . Выделим из
. Выделим из 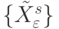 подмножество
подмножество  , отвечающее по
, отвечающее по 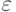 требованиям 1-й строки
требованиям 1-й строки 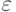 -спецификации (4.13), а по
-спецификации (4.13), а по  требованию "непрерывной" монотонности:
требованию "непрерывной" монотонности: 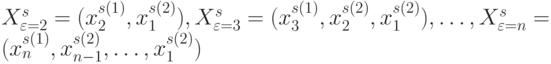 . Тогда для
. Тогда для  -значных входных векторов
-значных входных векторов 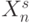 :
:
- с равнозначными компонентами
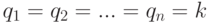 :
: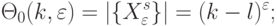
( 4.18) - с неравнозначными компонентами
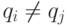 при
при 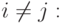
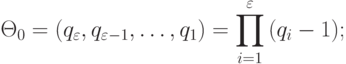
( 4.19) 
( 4.20)
Из (4.18)-(4.20) видно: мощность множества векторов 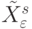 соответствует количеству
соответствует количеству  -транспозиций, порождаемых каждой образующей
-транспозиций, порождаемых каждой образующей  -транспозицией, соответствующего по ? столбца схемы (4.13), (4.15), если из
-транспозицией, соответствующего по ? столбца схемы (4.13), (4.15), если из  , а значит, и из
, а значит, и из 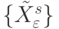 исключить вектора с кратными по
исключить вектора с кратными по  компонентами.
компонентами.
В приведенных выше  -транспозициях отсутствует транспозиция
-транспозициях отсутствует транспозиция 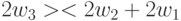 , в которой компоненты
, в которой компоненты  -кратны в данном случае образующей комбинации
-кратны в данном случае образующей комбинации 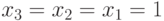 .
.
Отсюда, если компоненты  отвечают ограничению (4.10), то
отвечают ограничению (4.10), то
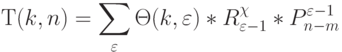 |
( 4.21) |
где 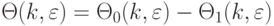 , а
, а 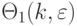 - количество
- количество 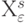 с
с  -кратными значениями
-кратными значениями 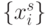 по отношению к некоторой образующей комбинации
по отношению к некоторой образующей комбинации 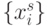 .
.
Чтобы выделить из 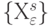 вектора с
вектора с  -кратными компонентами и рассчитать их количество
-кратными компонентами и рассчитать их количество 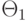 , построим вектора
, построим вектора  , у которых значность
, у которых значность 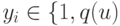 выбирается по правилу
выбирается по правилу ![q(u) = Е[(k -1)/u] \ge 1](/sites/default/files/tex_cache/3501721bfa3fcac36a045f7838bf2c6c.png) , где
, где  - простые числа из натурального ряда
- простые числа из натурального ряда 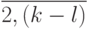 . В
табл. 4.5 приведены вектора
. В
табл. 4.5 приведены вектора  при
при 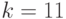 и
и 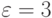 . В этом случае
. В этом случае 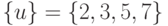 ,
, 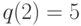 ,
, 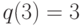 ,
,  ,
, 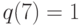 .
.
| u | 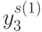 |
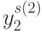 |
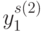 |
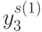 |
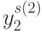 |
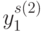 |
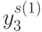 |
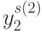 |
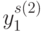 |
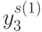 |
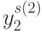 |
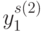 |
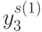 |
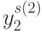 |
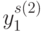 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 1 | 1 | 1 | 2 | 1 | 1 | 3 | 1 | 1 | 4 | 1 | 1 | 5 | 1 | 1 |
| 1 | 1 | 2 | 2 | 1 | 2 | 3 | 1 | 2 | 4 | 1 | 2 | 5 | 1 | 2 | |
| 1 | 1 | 3 | 2 | 1 | 3 | 3 | 1 | 3 | 4 | 1 | 3 | 5 | 1 | 3 | |
| 1 | 1 | 4 | 2 | 1 | 4 | 3 | 1 | 4 | 4 | 1 | 4 | 5 | 1 | 4 | |
| 1 | 1 | 5 | 2 | 1 | 5 | 3 | 1 | 5 | 4 | 1 | 5 | 5 | 1 | 5 | |
| 1 | 5 | 5 | 2 | 5 | 5 | 3 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | 5 | |
| 3 | 1 | 1 | 1 | 2 | 1 | 1 | 3 | 1 | 1 | ||||||
| 1 | 1 | 2 | 2 | 1 | 2 | 3 | 1 | 2 | |||||||
| 1 | 1 | 3 | 2 | 1 | 3 | 3 | 1 | 3 | |||||||
| 1 | 3 | 3 | 2 | 3 | 1 | 3 | 3 | 3 | |||||||
| 5 | 1 | 1 | 1 | 2 | 1 | 1 | |||||||||
| 1 | 1 | 2 | 2 | 1 | 2 | ||||||||||
| 1 | 2 | 1 | 2 | 1 | 1 | ||||||||||
| 1 | 2 | 2 | 2 | 2 | 2 | ||||||||||
| 7 | 1 | 1 | 1 |
Из данных
табл. 4.5 видно, что покомпонентное умножение векторов  на соответствующие им скаляры
на соответствующие им скаляры 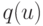 и порождает все
и порождает все 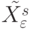 с
с  -кратными компонентами.
-кратными компонентами.
Поэтому при 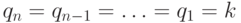 :
:
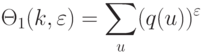 |
( 4.22) |
а при 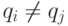 (
( 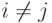 ):
):
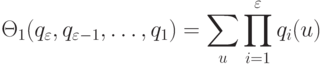 |
( 4.23) |
Численный анализ соотношений (4.22)-(4.23) для 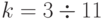 и
и 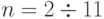 (табл. 4.6 и 4.7) показал:
(табл. 4.6 и 4.7) показал:
- При
 количество
количество  -транспозиций удовлетворяет неравенству
-транспозиций удовлетворяет неравенству 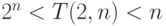 !, а количество
!, а количество  -транспозиций превосходит порядок группы
-транспозиций превосходит порядок группы  переименований компонент
переименований компонент 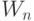 уже при
уже при  и при
и при 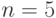 :
: 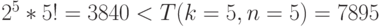 .
. - Количество
 -транспозиций
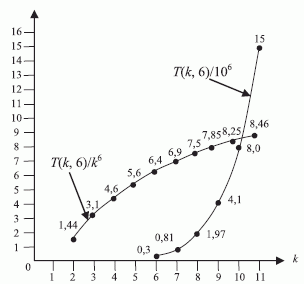
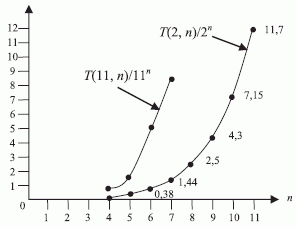
-транспозиций 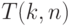 возрастает гораздо быстрее соответствующей степенной (рис. 4.26) и показательной (рис. 4.27) функции, причем вклад
возрастает гораздо быстрее соответствующей степенной (рис. 4.26) и показательной (рис. 4.27) функции, причем вклад  -источника превосходит вклад
-источника превосходит вклад  -источника не менее чем на два порядка при достаточно "малых"
-источника не менее чем на два порядка при достаточно "малых"  и
и  .
.
 |
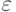 |
 |
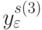 |
 |
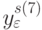 |
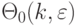 |
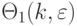 |
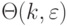 |
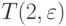 |
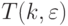 |
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 3 | 125 | 27 | 8 | 1 | 103 | 161 | 839 | 20 | 16780 |
| 4 | 625 | 81 | 16 | 1 | 104 | 723 | 9277 | 30 | 278310 | |
| 5 | 3125 | 243 | 32 | 1 | 105 | 3401 | 96599 | 30 | 2897970 | |
| 6 | 15625 | 729 | 64 | 1 | 106 | 16419 | 983581 | 12 | 11802972 | |
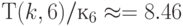 |
92 | 14996032 | ||||||||
| 10 | 3 | 64 | 27 | 8 | 1 | 93 | 100 | 629 | 20 | 12580 |
| 4 | 256 | 81 | 16 | 1 | 94 | 354 | 6207 | 30 | 186210 | |
| 5 | 1024 | 243 | 32 | 1 | 95 | 1300 | 57749 | 30 | 1732470 | |
| 6 | 4096 | 729 | 64 | 1 | 96 | 4890 | 526551 | 12 | 6318612 | |
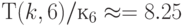 |
92 | 8249872 | ||||||||
| 9 | 3 | 64 | 8 | 1 | 83 | 74 | 438 | 20 | 8760 | |
| 4 | 256 | 16 | 1 | 84 | 274 | 3822 | 30 | 114660 | ||
| 5 | 1024 | 32 | 1 | 85 | 1058 | 31710 | 30 | 951300 | ||
| 6 | 4096 | 64 | 1 | 86 | 4162 | 257982 | 12 | 3095784 | ||
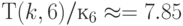 |
92 | 4170504 | ||||||||
| 8 | 3 | 27 | 8 | 1 | 73 | 37 | 306 | 20 | 6120 | |
| 4 | 81 | 16 | 1 | 74 | 99 | 2302 | 30 | 69060 | ||
| 5 | 243 | 32 | 1 | 75 | 277 | 16530 | 30 | 495900 | ||
| 6 | 729 | 64 | 1 | 76 | 795 | 116854 | 12 | 1402248 | ||
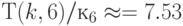 |
92 | 1973328 | ||||||||
| 7 | 3 | 27 | 8 | 63 | 36 | 180 | 20 | 3600 | ||
| 4 | 81 | 16 | 64 | 98 | 1198 | 30 | 35940 | |||
| 5 | 243 | 32 | 65 | 276 | 7500 | 30 | 225000 | |||
| 6 | 729 | 64 | 66 | 794 | 45862 | 12 | 550344 | |||
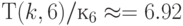 |
92 | 814884 | ||||||||
| 6 | 3 | 8 | 1 | 53 | 10 | 115 | 20 | 2300 | ||
| 4 | 16 | 1 | 54 | 18 | 607 | 30 | 18210 | |||
| 5 | 32 | 1 | 55 | 34 | 3091 | 30 | 92730 | |||
| 6 | 64 | 1 | 56 | 66 | 15559 | 12 | 186708 | |||
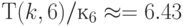 |
92 | 299948 | ||||||||
| 5 | 3 | 8 | 1 | 43 | 9 | 55 | 20 | 1100 | ||
| 4 | 16 | 1 | 44 | 17 | 239 | 30 | 7170 | |||
| 5 | 32 | 1 | 45 | 33 | 991 | 30 | 29730 | |||
| 6 | 64 | 1 | 46 | 65 | 4031 | 12 | 48372 | |||
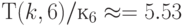 |
92 | 86372 | ||||||||
| 4 | 3 | 1 | 1 | 33 | 2 | 25 | 20 | 500 | ||
| 4 | 1 | 1 | 34 | 2 | 79 | 30 | 2370 | |||
| 5 | 1 | 1 | 35 | 2 | 241 | 30 | 7230 | |||
| 6 | 1 | 1 | 36 | 2 | 727 | 12 | 8724 | |||
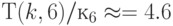 |
92 | 18824 | ||||||||
| 3 | 3 | 1 | 23 | 1 | 7 | 20 | 140 | |||
| 4 | 1 | 24 | 1 | 15 | 30 | 450 | ||||
| 5 | 1 | 25 | 1 | 31 | 30 | 930 | ||||
| 6 | 1 | 26 | 1 | 63 | 12 | 756 | ||||
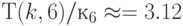 |
92 | 2276 | ||||||||
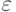 |
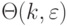 |
 |
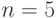 |
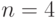 |
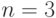 |
||||
|---|---|---|---|---|---|---|---|---|---|
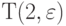 |
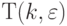 |
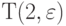 |
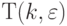 |
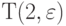 |
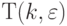 |
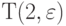 |
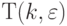 |
||
| Y | 839 | 20 | 16780 | 10 | 8390 | 4 | 3356 | 1 | 839 |
| 4 | 9277 | 30 | 278310 | 10 | 92770 | 2 | 18554 | - | - |
| 5 | 96599 | 30 | 2897970 | 5 | 482995 | - | - | - | - |
| 6 | 983581 | 12 | 11802972 | - | - | - | - | - | - |
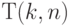 |
92 | 14996032 | 25 | 584155 | 6 | 21910 | 1 | 839 | |
Отвечающий утверждению 2  -источник срабатывает независимо от
-источник срабатывает независимо от  -источника, когда
-источника, когда 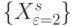 порождается из
порождается из 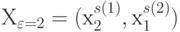 подстановками
подстановками 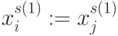 и
и 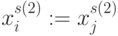 , в которых:
, в которых:
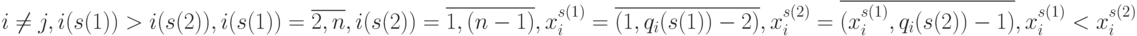 |
( 4.24) |
Ограничениям (4.24) удовлетворяет 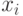 -спецификация:
-спецификация:
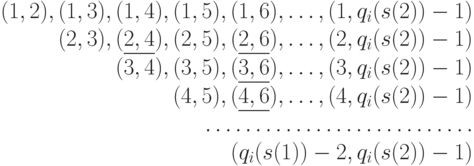 |
( 4.25) |
в которой:
- каждая строка идентифицируется значением
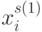 , а каждый столбец - значением
, а каждый столбец - значением 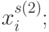
- каждому элементу отвечает
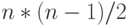 подстановок
подстановок 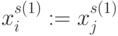 ,
,  ,
(
,
( 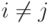 );
); - в) имеется множество
 -кратных комбинаций
(
-кратных комбинаций
( 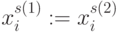 ) (подчеркнуты в (4.25)), мощность которого задается
) (подчеркнуты в (4.25)), мощность которого задается 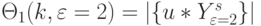 с параметрами:
с параметрами:- при
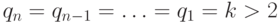 :
:  - простые числа из натурального ряда
- простые числа из натурального ряда![\overline{2,E[(k-l)/2]},\, y_i^{s(1)} = \overline{1,(q(u)-l)},\, y^{s(2)}_i=\overline{2,q(u)},
q(u)=E[(k-l)/u_i];](/sites/default/files/tex_cache/5af41d3632c66c0199b71a5ad8342ded.png)
- при
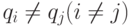 :
: 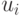 - простые числа из натурального ряда
- простые числа из натурального ряда![\overline{2,E[(q_i-l)/2]},\, y_i^{s(1)} = \overline{1,(q(u_i)-l)},\, y^{s(2)}_i=\overline{2,q(u_i)},
q(u_i)=E[(q_i-l)/u_i]](/sites/default/files/tex_cache/17e842876064710b461268494a54f94d.png)
- при
Из (4.25) видно, что количество  -транспозиций значений свертки
-транспозиций значений свертки  при ограничении (4.10) на компоненты весового вектора определяется:
при ограничении (4.10) на компоненты весового вектора определяется:
- для равнозначных
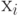 :
:![T(k,\varepsilon=2) = (n*(n-1)/2)*[\Theta_0(k,\varepsilon=2) - \Theta(k,\varepsilon=2)] = \\
n*(n-1) *[k*(k-1) - \sum_u{q(u)*(q(u)-1)}] / 4](/sites/default/files/tex_cache/95c92a12e7b05e410d43cd01714af65e.png)
- для неравнозначных
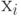 :
:![T(q_2,q_1,\varepsilon=2) = 0.5 \sum_{i(1),i(2)}[q_{i(2)}*(q_{i(2)} - 1) - \xi(q_{i(2)} - q_{i(1)}) *(q_{i(2)} - q_{i(1)} -1) - \\
\sum_{u_i}{q(u_{i(2)})*(q(u_{i(2)}) -1) - \xi(q(u_{i(2)}) - q(u_{i(1)})) *(q(u_{i(2)}) - q(u_{i(1)}) -1)} ]](/sites/default/files/tex_cache/3a4c1e212a287656e935bd24491641a5.png)
где
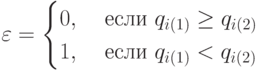
Таким образом, оператору линейной свертки входных векторов в (4.4) соответствует комбинаторная схема порождения транспозиций вида:
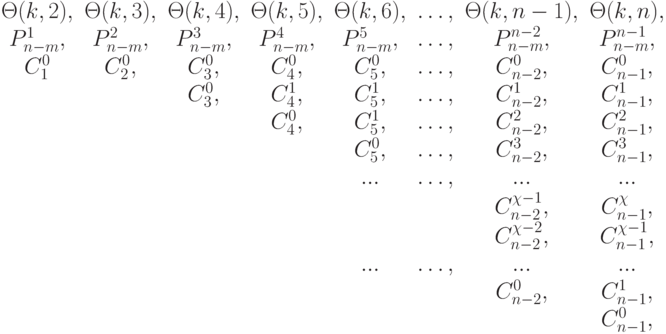 |
( 4.26) |
где 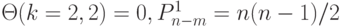
Из принятых соглашений следует: в каждой транспозиции неравенство 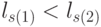 соответствует лексикографическому порядку следования значений свертки на скалярной оси
соответствует лексикографическому порядку следования значений свертки на скалярной оси  , а переход к противоположному неравенству при непрерывном сканировании в пространстве значений весового вектора происходит после выполнения равенства
, а переход к противоположному неравенству при непрерывном сканировании в пространстве значений весового вектора происходит после выполнения равенства 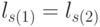 .
.
Отсюда, все точки, принадлежащие граням (гипер)пирамид, задающих границы индексных зон в пространстве значений 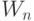 , нарушают условие (4.11) линейной независимости
, нарушают условие (4.11) линейной независимости 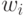 в (4.10), а значит, и условие изоморфизма в отображении
в (4.10), а значит, и условие изоморфизма в отображении 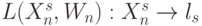 . В частности, на
рис. 4.23 условию
. В частности, на
рис. 4.23 условию  отвечают точки плоскости
отвечают точки плоскости 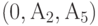 , а условию
, а условию  - точки плоскости
- точки плоскости 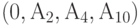 и т. д. Это говорит о том, что на границах индексных зон различные вектора
и т. д. Это говорит о том, что на границах индексных зон различные вектора 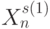 и
и 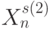 имеют общий гомоморфный скалярный образ, что делает их неразличимыми методами пороговой логики, использующими в качестве входного преобразования оператор линейной свертки входных векторов (прообразов).
имеют общий гомоморфный скалярный образ, что делает их неразличимыми методами пороговой логики, использующими в качестве входного преобразования оператор линейной свертки входных векторов (прообразов).
В 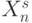 кроме
кроме  -кратности имеется еще и
-кратности имеется еще и  -кратность, которая тиражирует рассмотренные
-кратность, которая тиражирует рассмотренные  -и
-и  -транспозиции на
-транспозиции на 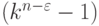 комбинаций векторов
комбинаций векторов 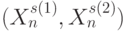 , в которых
, в которых 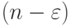 компонент
компонент 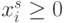 одновременно принадлежат левой и правой части неоднозначного неравенства
одновременно принадлежат левой и правой части неоднозначного неравенства  .
.
Например, для булевых векторов с 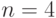
 -транспозиция
-транспозиция 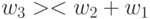 тиражируется на
тиражируется на  -кратную транспозицию
-кратную транспозицию 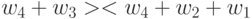 , а
, а  -транспозиция
-транспозиция 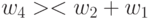 тиражируется на транспозицию
тиражируется на транспозицию 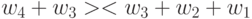 .
В результате в первом случае одновременно с < всегда реализуется
.
В результате в первом случае одновременно с < всегда реализуется 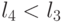 , а во втором
, а во втором 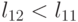 случае одновременно с
случае одновременно с 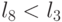 всегда реализуется
всегда реализуется 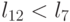 .
.
В случае  -мерных булевых векторов
-мерных булевых векторов 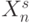 все проекции индексных зон на плоскости
все проекции индексных зон на плоскости 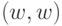 имеют одинаковую "площадь" и, как следствие, обеспечивают равноустойчивую систему решающих правил по отношению к флуктуациям
имеют одинаковую "площадь" и, как следствие, обеспечивают равноустойчивую систему решающих правил по отношению к флуктуациям 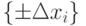 и
и  реальных физических величин
реальных физических величин  и
и  . Для
. Для  -значных входных векторов равенство таких "площадей" нарушается, а структура неравномерного разбиения
-значных входных векторов равенство таких "площадей" нарушается, а структура неравномерного разбиения 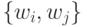 проекциями
проекциями  -мерных индексных зон определяется не только
-мерных индексных зон определяется не только  -значностью
-значностью 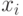 и
и 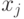 , но и правилом кодирования
, но и правилом кодирования 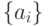 и
и 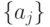 (
( 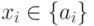 ,
, 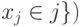 , от которого зависит количество
, от которого зависит количество 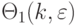
 -кратных комбинаций
-кратных комбинаций 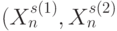 ) в (4.21) и (4.26). Например, при
) в (4.21) и (4.26). Например, при  и кодировании
и кодировании 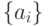 числами натурального ряда 0,5 из состава М-транспозиций исключается комбинация (
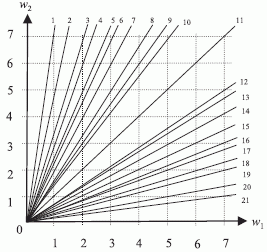
числами натурального ряда 0,5 из состава М-транспозиций исключается комбинация ( 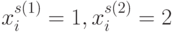 ) (рис. 4.28). При кодировании
) (рис. 4.28). При кодировании 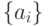 простыми числами (рис. 4.29) такая кратная комбинация отсутствует. В результате не только возрастает количество проекций индексных зон на плоскости
простыми числами (рис. 4.29) такая кратная комбинация отсутствует. В результате не только возрастает количество проекций индексных зон на плоскости 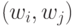 , но и более неравномерно распределяется "площадь" между ними.
, но и более неравномерно распределяется "площадь" между ними.
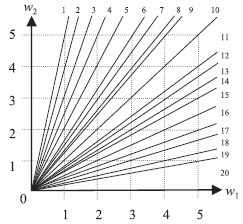
Рис. 4.28. Структура индексных зон (n=2; q_{2}=q_{1}=6) при кодировании x_{i} числами натурального ряда
Отсюда можно заключить:
- Неизбыточное сканирование в пространстве значений
 , обеспечивающее однократное попадание в каждую индексную зону, необходимо выполнять с переменным шагом
, обеспечивающее однократное попадание в каждую индексную зону, необходимо выполнять с переменным шагом  , что требует соответствующей стратегии управления таким сканированием даже в случае полного перебора всех индексных зон.
, что требует соответствующей стратегии управления таким сканированием даже в случае полного перебора всех индексных зон.
- При прочих равных условиях правило кодирования входных переменных с большим количеством индексных зон порождает и большое количество транспозиций, что позитивно сказывается на разнообразии реализуемых (М)ПМ ЛФ, но при этом, вообще говоря, снижается устойчивость минимально пороговой реализации отдельных ЛФ.
- Знание структуры индексных зон позволяет отказаться от их полного перебора и реализовать их "перечисление" в произвольном порядке, согласованном со стратегией поиска минимально пороговой реализации заданной ЛФ.
Введенные комбинаторные схемы и отвечающие им численные соотношения:
- могут быть положены в основу алгебраической теории формальных нейронов, так как базируются на преобразованиях, сохраняющих отношение порядка между значениями свертки входных векторов при вариациях весового вектора внутри индексной зоны, что приводит к преобразованиям подстановки и перечислительным процедурам классического комбинаторного анализа [90];
- генерируют полное множество кратных транспозиций значений свертки входных векторов без априорного знания характеристик точности и стратегии управления приращениями компонент весового вектора, что позволяет решать задачи абстрактного анализа и синтеза сетей из формальных нейронов как чисто дискретные, формируя систему ограничений на компоненты весового вектора, удовлетворяющего условию минимальной пороговой реализации заданной логической функции;
- подтверждают, что устойчивость решающих правил в системах распознавания образов многопорогового типа и в сетях из формальных нейронов зависит от правил кодирования входных переменных и вступает в противоречие с функциональным разнообразием реализуемых отображений типа "вход-выход" при одинаковых ограничениях на размерность вектора порогов и возможности перестройки его компонент;
- показывают, что традиционные для систем реального времени методы квантования непрерывных входных сигналов, обусловленные необходимостью сохранения некоторой меры, индуцируют в сопряженном [91] пространстве весовых векторов принципиально иной тип дискретности, обусловленный необходимостью сохранения отношения порядка между значениями свертки входных сигналов;
- позволяют проводить абстрактный синтез (много)пороговых моделей "нечисленными" методами и средствами, оперирующими системами неравенств, проверка совместности которых требует тривиальной "измерительной системы" типа рычажных весов.