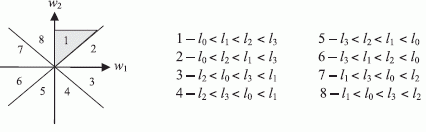| Россия, Москва, МЭИ, 2006 |
Нейрофизиологический и формально-логический базис нейроподобных вычислений
4.5. Многопороговые модели
Рассмотренные формальные модели нейронов и нейронных структур типа перцептрона в своей основе используют некоторые пороговые правила "принятия решений" на этапе формирования выходной реакции, для исследования которых был разработан аппарат пороговой логики [77]. В рамках этой теории классическую (много)пороговую модель формального нейрона, которая отражает основные электрофизиологические свойства реального нейрона [56], можно представить в импликативной форме:
![(l_s(X_n^s,W_{n}) = \sum_{i=1}^n{x_i^s *w_{i})\in (h_{j-1},h_j]\Rightarrow f_{s} := b_j.](/sites/default/files/tex_cache/28dd71468374fa5c9d8bc1f31e9040a8.png) |
( 4.4) |
Здесь 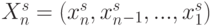 -
-  -мерный входной вектор с компонентами
-мерный входной вектор с компонентами 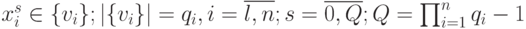 ; компоненты "весового" вектора
; компоненты "весового" вектора  принимают значения
принимают значения  ; индекс
; индекс  представляет ранг значения свертки
представляет ранг значения свертки 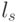 (и однозначно связанного с ним вектора
(и однозначно связанного с ним вектора 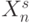 ) на скалярной оси
) на скалярной оси  ;
;  - значения реализуемой логической функции
- значения реализуемой логической функции 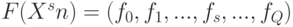 ;
;  ;
; 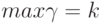 ;
;  , а вектор порогов
, а вектор порогов 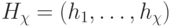 разбивает множество
разбивает множество  скалярных произведений входного и "весового" векторов на
скалярных произведений входного и "весового" векторов на 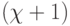 пороговых полуинтервалов
пороговых полуинтервалов ![( h_{j-1},h_j]](/sites/default/files/tex_cache/67a8d61552924149b99062259f1175fc.png) ;
;  ;
; 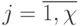 ;
;  ;
;  - отношение следования;
- отношение следования;  - оператор подстановки (присваивания).
- оператор подстановки (присваивания).
В отличие от формального нейрона Мак-Каллока - Питтса функциональная полнота многопороговых элементов и их моделей достигается только параметрической адаптацией, то есть вариацией весового  и/или порогового
и/или порогового 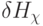 векторов.
векторов.
Если в (4.4) ввести ограничения на весовые коэффициенты типа  , то получим систему мажоритарных пороговых правил формального нейрона Мак-Каллока - Питтса, а если зафиксировать систему связей между пороговыми элементами по типу "каждый с каждым", получим перцептрон Розенблатта.
, то получим систему мажоритарных пороговых правил формального нейрона Мак-Каллока - Питтса, а если зафиксировать систему связей между пороговыми элементами по типу "каждый с каждым", получим перцептрон Розенблатта.
Задачи оптимального синтеза (много)пороговых моделей сформулированы В.И. Варшавским (предисловие к [77]):
- Нахождение условий реализуемости произвольной логической функции той или иной многопороговой моделью.
- Синтез многопороговой модели по заданной логической функции и некоторому критерию качества.
- Синтез сети из многопороговых моделей по заданной логической функции и некоторому критерию качества.
Характеристики структурной сложности,связывающие задачи 1-3 в единую схему оптимального синтеза многопороговых моделей, введены Л.А. Шоломовым [78]:
- сложность (много)пороговой модели:
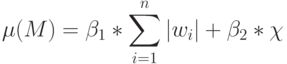
( 4.5) где
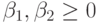 - некоторые одновременно не равные нулю "стоимостные" коэффициенты реализации "единицы" веса и одного порога соответственно;
- некоторые одновременно не равные нулю "стоимостные" коэффициенты реализации "единицы" веса и одного порога соответственно; - сложность логической функции
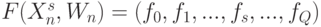 :
:
( 4.6) где минимум берется по всем многопороговым моделям типа (4.4);
- сложность класса логических функций
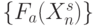 (функция Шеннона):
(функция Шеннона):
( 4.7) где максимум берется по всем
 -значным логическим функциям
-значным логическим функциям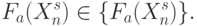
В такой постановке, как и в любой задаче поисковой оптимизации, основная сложность связана с реализацией критерия (4.7), который требует полного перебора всех логических функций из некоторого класса, а основная трудность связана с неопределенностью выбора шага вариации 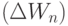
 -мерного весового вектора
-мерного весового вектора 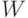 .
.
Решая методом случайного поиска задачи оптимального синтеза (много)пороговых моделей, А.Т. Бахарев и Л.А. Растригин [79] обнаружили, что с позиций поиска минимума размерности вектора порогов 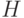 значение имеют только те вариации весового вектора
значение имеют только те вариации весового вектора 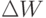 , которые нарушают отношение порядка (по индексу
, которые нарушают отношение порядка (по индексу  ) между значениями свертки
) между значениями свертки 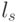 на скалярной оси
на скалярной оси 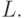 Например, для
Например, для 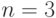 и
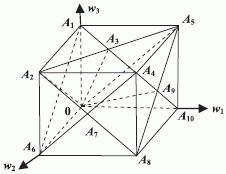
и 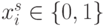 (рис. 4.23) вариации весового вектора
(рис. 4.23) вариации весового вектора  в пределах пирамид с вершиной в начале координат и
с основаниями
в пределах пирамид с вершиной в начале координат и
с основаниями 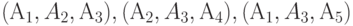 и т. д.
дают фиксированный порядок следования индексов
и т. д.
дают фиксированный порядок следования индексов  , упорядоченных по возрастанию значений свертки
, упорядоченных по возрастанию значений свертки 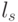 :
: 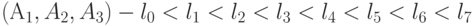 ,
, 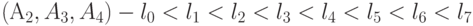 ,
, 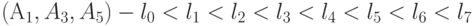 .
.
Вариации весового вектора 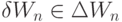 , которые сохраняют отношение порядка (по индексу
, которые сохраняют отношение порядка (по индексу  ) между значениями свертки
) между значениями свертки 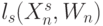 , получили название индексных зон [79]. Они позволяют заменить непрерывные вариации
, получили название индексных зон [79]. Они позволяют заменить непрерывные вариации  конечным набором целочисленных значений
конечным набором целочисленных значений  , отвечающих одному и тому же порядку следования индексов
, отвечающих одному и тому же порядку следования индексов  , и разбить весь процесс оптимального синтеза формальных нейронов на два этапа:
, и разбить весь процесс оптимального синтеза формальных нейронов на два этапа:
- абстрактно-логический, который осуществляется на множестве подстановок индексов
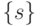 и где определяются условия минимально пороговой реализации (много)пороговой модели;
и где определяются условия минимально пороговой реализации (много)пороговой модели; - "физический", который обеспечивает переход от
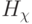 , заданным на упорядоченном целочисленном множестве
, заданным на упорядоченном целочисленном множестве 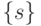 , к
, к 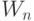 и
и 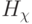 с непрерывными значениями компонент.
с непрерывными значениями компонент.
Работу (много)пороговой модели ((М)ПМ) типа (4.4) проиллюстрируем на примере ее настройки на реализацию булевых функций (БФ) двух переменных 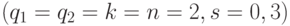 :
"И" -
:
"И" - 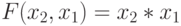 ;
"ИЛИ" -
;
"ИЛИ" - 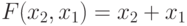 ;
"НЕРАВНОЗНАЧНОСТЬ" -
;
"НЕРАВНОЗНАЧНОСТЬ" - 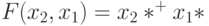 ,
и в предположении
,
и в предположении  ,
, 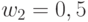 . В этом случае значения свертки двумерных булевых
. В этом случае значения свертки двумерных булевых  -векторов
-векторов 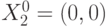 ,
, 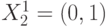 ,
, 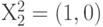 и
и 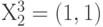 расположатся на скалярной оси
расположатся на скалярной оси  в лексикографическом (по индексу
в лексикографическом (по индексу  ) порядке:
) порядке:
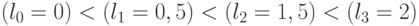 |
( 4.8) |
Отсюда, для настройки (М)ПМ на реализацию:
- БФ "И" необходимо, чтобы одномерный вектор порогов удовлетворял условию
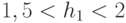 , а правило подстановки значений функции над двумя пороговыми полуинтервалами имело вид:
, а правило подстановки значений функции над двумя пороговыми полуинтервалами имело вид: 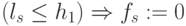 ,
,  ;
; - БФ "ИЛИ" необходимо, чтобы при сохранившемся правиле подстановки одномерный вектор порогов принимал значение
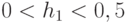 ;
; - БФ "НЕРАВНОЗНАЧНОСТЬ" необходимо, чтобы вектор порогов был двумерным с компонентами
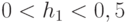 и
и 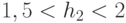 , а прави-ло подстановки значений над тремя пороговыми полуинтервалами имело вид
, а прави-ло подстановки значений над тремя пороговыми полуинтервалами имело вид 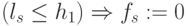 ;
; 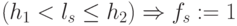 ;
;  .
.
Вариации значений компонент весового вектора, размерности и значений компонент вектора порогов обеспечивают реализацию произвольной ЛФ  переменных, причем не каждая вариация весового вектора изменяет отношение порядка (по индексу
переменных, причем не каждая вариация весового вектора изменяет отношение порядка (по индексу  ) между значениями свертки на скалярной оси
) между значениями свертки на скалярной оси  . Так, при
. Так, при 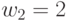 и
и 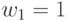 лексикографический порядок сохранится:
лексикографический порядок сохранится: 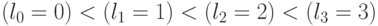 , а при
, а при  и
и  он нарушится:
он нарушится:
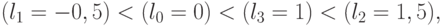 |
( 4.9) |
то есть вместо порядка следования индексов  вида
вида 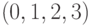 в (4.8) получили порядок следования
в (4.8) получили порядок следования 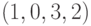 в (4.9).
в (4.9).
Такой "перестановочный" эффект значений свертки на оси  служит источником минимизации размерности вектора порогов или, что одно и то же, системы решающих правил в (М)ПМ. Например, для БФ
служит источником минимизации размерности вектора порогов или, что одно и то же, системы решающих правил в (М)ПМ. Например, для БФ 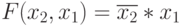 при лексикографическом порядке требуется (М)ПМ с двумя порогами
при лексикографическом порядке требуется (М)ПМ с двумя порогами 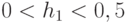 и
и 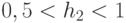 , а при порядке следования (4.9) - с одним порогом
, а при порядке следования (4.9) - с одним порогом 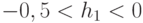 и системой решающих правил
и системой решающих правил 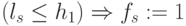 ,
,  .
.
В [79,
80] проанализированы условия эквивалентного перехода от (М)ПМ с аналоговыми параметрами
( 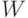 и
и 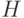 ) к (М)ПМ с дискретными параметрами. Было показано, что перестройка входного преобразования (М)ПМ, связанная с вариациями
) к (М)ПМ с дискретными параметрами. Было показано, что перестройка входного преобразования (М)ПМ, связанная с вариациями  весового вектора, приводит к различным
весового вектора, приводит к различным  -перестановкам упорядоченных компонент свертки
-перестановкам упорядоченных компонент свертки 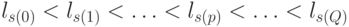 на скалярной оси
на скалярной оси 
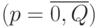 . В результате полная вариация весового вектора
. В результате полная вариация весового вектора 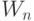 порождает множество
порождает множество  перестановок значений компонент свертки
перестановок значений компонент свертки  и связанных с ними индексов
и связанных с ними индексов  , что и позволяет разбить все пространство
, что и позволяет разбить все пространство 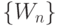 на классы эквивалентности
на классы эквивалентности 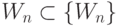 , такие, что вариации
, такие, что вариации  внутри класса
внутри класса  не нарушают связанного с этим классом отношения порядка между значениями компонент свертки.
не нарушают связанного с этим классом отношения порядка между значениями компонент свертки.
Структура пространства индексных зон (ИЗ) или, что одно и то же, вариации 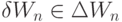 , сохраняющие отношение порядка
, сохраняющие отношение порядка  , зависит от размерности
, зависит от размерности  входного вектора
входного вектора 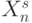 и значности
и значности  его компонент, что иллюстрирует
рис. 4.24 [79,
80], где показаны все восемь индексных зон для
его компонент, что иллюстрирует
рис. 4.24 [79,
80], где показаны все восемь индексных зон для 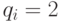 . Из
рис. 4.24 видна центрально-осевая симметрия пространства индексных зон, что позволяет ограничить анализ их структуры только первым (гипер)октантом.
. Из
рис. 4.24 видна центрально-осевая симметрия пространства индексных зон, что позволяет ограничить анализ их структуры только первым (гипер)октантом.
Если в трехмерном случае индексные зоны представляют собой пирамиды с вершинами в начале координат, то в двумерном случае это уже сектора, заключенные между наклонными линиями на целочисленной решетке, которая задается значениями компонент входного вектора 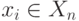 .
.
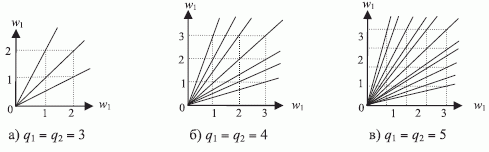
Равномерность разбиения пространства 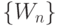 на индексные зоны нарушается уже при
на индексные зоны нарушается уже при 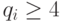 (рис. 4.25), что приводит к разно "устойчивой" реализации ЛФ, зависящей от выбранного значения весового вектора.
(рис. 4.25), что приводит к разно "устойчивой" реализации ЛФ, зависящей от выбранного значения весового вектора.
Из сказанного следует, при фиксированном векторе порогов 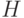 и правиле подстановки
и правиле подстановки 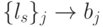 вариации весового вектора
вариации весового вектора 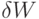 внутри индексной зоны изменяют значения
внутри индексной зоны изменяют значения  , но не нарушают отношение порядка между ними, а значит, и задаваемое (4.4) правило реализации ЛФ. Например, в заштрихованной индексной зоне (рис. 4.2) отношение порядка имеет вид
, но не нарушают отношение порядка между ними, а значит, и задаваемое (4.4) правило реализации ЛФ. Например, в заштрихованной индексной зоне (рис. 4.2) отношение порядка имеет вид 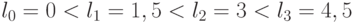 .
Здесь для определенности указаны значения
.
Здесь для определенности указаны значения 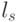 отвечающие
отвечающие 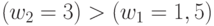 . Тогда при
. Тогда при  реализуется ЛФ "И"
реализуется ЛФ "И" 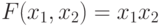 , если правило подстановки имеет вид
, если правило подстановки имеет вид 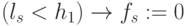 ,
,  . Переход в индексную зону с номером 2 сопровождается инверсией неравенства
. Переход в индексную зону с номером 2 сопровождается инверсией неравенства 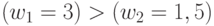 , которая приводит к новому порядку следования
, которая приводит к новому порядку следования 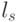 на скалярной оси
на скалярной оси 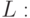
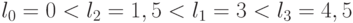 . Однако он не нарушает правила подстановки, задаваемые функцией "И". Если (М)ПМ настроен на ЛФ
. Однако он не нарушает правила подстановки, задаваемые функцией "И". Если (М)ПМ настроен на ЛФ 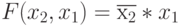 то такая же вариация весового вектора (при неизменном правиле подстановки
то такая же вариация весового вектора (при неизменном правиле подстановки 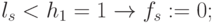
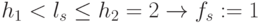 ; и
; и  ) приведет к реализации ЛФ
) приведет к реализации ЛФ 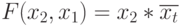 .
.
Таким образом, с позиций устойчивой реализации заданной функции 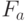 вида (4.4) необходимо как минимум сохранить отношение порядка (при фиксированном правиле разбиения
вида (4.4) необходимо как минимум сохранить отношение порядка (при фиксированном правиле разбиения  и правиле подстановки
и правиле подстановки 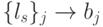 ), а при перестройке (М)ПМ с одной функции на другую при той же системе решающих правил надо перейти в другую ИЗ, то есть изменить отношение порядка.
), а при перестройке (М)ПМ с одной функции на другую при той же системе решающих правил надо перейти в другую ИЗ, то есть изменить отношение порядка.