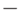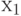| Россия, Москва, МЭИ, 2006 |
Междисциплинарный характер компьютерных проектов
1.1. Научно-технические и социально-экономические предпосылки зарождения вычислительных технологий
Пик дискуссий о роли и месте кибернетики и вычислительной техники в обществе пришелся на середину 50-60-х годов прошлого столетия [1,2] и был ориентирован на оценку перспектив их использования. Отсутствие видимого прогресса в области промышленно освоенных нанотехнологий, несмотря на 25-летние интернациональные усилия в этой области и многомиллиардные затраты, вынуждают провести теперь уже ретроспективный анализ причин и предпосылок, которые обусловили успешное завершение беспрецедентного по масштабам и результатам того времени междисциплинарного проекта.
Появление кибернетики и вычислительной техники в середине 40-х годов прошлого столетия было обусловлено целым рядом факторов, требовавших повышения скорости вычислений. Простейший способ ускорения вычислений - это выполнение действий на бумаге в столбик. Однако со временем такого ускорения оказалось недостаточно для расчета различного рода строительных и подвижных механических конструкций, что привело к созданию арифмометра, способного механически выполнять арифметические действия над десятичными числами. Механический арифмометр повысил производительность вычислений в несколько раз. Но в 30-х годах прошлого столетия и такая скорость оказалась недостаточной, что привело к "автоматизации" процесса выполнения отдельных арифметических действий. Осуществить такую "автоматизацию" удалось благодаря успехам электротехники, когда к механическому арифмометру добавили электрический привод и электромеханические средства автоматики, обеспечившие выполнение циклической последовательности элементарных действий в алгоритмах умножения и деления десятичных чисел. В итоге удалось довести скорость вычислений до 1 операции за 2-5 секунд.
Вторая мировая война поставила человеческие жизни и накопленные человечеством материальные и культурные ценности в прямую зависимость от умения быстро и точно вычислять: кто быстрее и точнее принимал решения в зенитных и артиллерийских противоборствах на суше, море и в воздухе, тот и побеждал.
С позиций вычислительной техники сущность проблемы состояла в следующем. Возросшие скорости перемещения боевой техники (в первую очередь самолетов и танков) повысили их маневренность на поле боя, что требовало повышения эффективности средств противодействия (зенитных и артиллерийских орудий), и в первую очередь на этапе прицеливания. Стрельба по подвижным целям требует определения в темпе реального времени "точки встречи" средства поражения (снаряда в кинетическом оружии) с целью. В свою очередь, достоверный расчет "точки встречи" требует учета целого ряда "случайных" факторов: скорости, ускорения и траектории движения цели, направления и скорости ветра, взаимного начального расположения цели и орудия и т. п. В итоге наводчику зенитного орудия необходимо было в течение нескольких секунд вычислить ( экстраполировать ) "точку встречи", направить на нее орудие и осуществить выстрел. На охоте за утками такая задача разрешима и решается охотником линейной экстраполяцией на 2-3 корпуса утки вперед. Успех такой стрельбы предопределен несопоставимой скоростью взлета утки и полета дроби, а также относительно малой дальностью стрельбы (50-100 метров), что в совокупности лишает утку возможности эффективного маневра и уклонения от встречи со средством поражения.
В случае самолета периода Второй мировой войны разность скоростей со снарядом уже была не так велика, а дальность стрельбы достигала нескольких километров, что позволяло летчику осуществлять плохо предсказуемые и поэтому достаточно эффективные противозенитные маневры. В итоге одна из наиболее развитых в мире система противовоздушной обороны (ПВО) Англии оказалась малоэффективной, а ее радиотехнические средства оказались способны решить достаточно ограниченную задачу раннего предупреждения о нападении. В итоге на начальном этапе войны Англия понесла значительные потери среди мирного населения (Ковентри), что несовместимо с основополагающими принципами построения и существования вооруженных сил любой страны, требующих, чтобы потери среди мирного населения были несопоставимо более низкими, чем в армии.
Отсюда и встала жизненно важная задача экстраполяции в темпе реального времени случайного процесса и достоверного вычисления "точки встречи" снаряда и цели. Она потребовала увеличить производительность вычислительных средств на несколько порядков и включить их в состав контура управления "радиолокационная станция - зенитные орудия".
Автор кибернетики Н. Винер, решая эту задачу, исходил из следующего. Точную экстраполяцию положения самолета выполнить невозможно, так как с точки зрения артиллериста траектория самолета носит случайный характер. Но при стрельбе зенитным снарядом нулевая ошибка наведения и не требуется, так как имеется коническая область разлета осколков, а не одна точка поражения, а значит, и встречи цели и снаряда. Более того, траектория полета самолета не совсем случайная и ограничена такими факторами, как перегрузка летчика, инерционность системы управления, прочность летательного аппарата и т. п. Поэтому неопределенность в будущем положении самолета можно оценить приближенно с помощью статистических методов, то есть на основе предыстории наблюдения траектории полета.
Заслуга Н. Винера как раз и состояла в том, что он отказался от требования стопроцентного поражения самолета и стал решать задачу по критерию максимальной вероятности поражения цели. Однако методы экстраполяции случайных процессов требовали колоссальных по тем временам объемов вычислений, которые необходимо было осуществить в темпе реального времени, то есть в течение нескольких десятков секунд наблюдения за траекторией полета. Выполнить такой объем вычислений на электромеханических арифмометрах практически было невозможно, даже распределив работу между коллективом вычислителей, которые должны были координировать свои действия и обмениваться информацией друг с другом по ходу выполнения алгоритма вычислений.
Отсюда, прежде чем автоматизировать процесс наведения зенитного орудия на цель необходимо было:
- автоматизировать процесс управления ходом вычислений;
- использовать качественно новое вычислительное оборудование, работающее с производительностью порядка нескольких десятков тысяч операций в секунду, что требовало использования в вычислительной технике принципиально новых физико-технических принципов работы аппаратуры.
С позиций автоматизации вычислительный процесс представляет собой заданную программистом и корректируемую содержимым потоков обрабатываемых данных частично упорядоченную во времени последовательность арифметико-логических действий, которые необходимо выполнить на том или ином вычислительном устройстве над входными и промежуточными данными, чтобы получить требуемый результат вычислений. Поэтому автоматизация управления ходом вычислений прежде всего требовала формализации понятия алгоритма. Такая формализация была проведена к началу 30-х годов прошлого столетия для решения "внутренних" проблем математики. Поэтому Н. Винеру и его современникам осталось только материализовать требования формальных определений и понятий, которые интуитивно сводились к следующему.
Алгоритм должен представлять собой конечный набор правил выполнения некоторой процедуры, которая удовлетворяет трем главным требованиям:
- 1. Массовость, которая гарантирует выполнение не одной конкретной процедуры, а целого класса однородных и однотипных процедур.
Например, процедура вызова абонента телефонной сети регламентирует правила набора номера "вообще" и не зависит от конкретного номера абонента.
- Детерминированность,которая гарантирует однозначное понимание каждой инструкции алгоритма, что гарантирует воспроизводимость результатов вычислений, если они выполнены над одними и теми же входными данными. В нашем случае правильная связь с нужным абонентом будет всегда установлена, если исключить ошибки набора и идентификации его номера.
-
Результативность,которая гарантирует конечность применения отдельных инструкций и алгоритма в целом. В случае экстраполяции траектории полета самолета результат должен быть получен за конечное число шаговгде
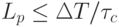
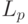 - количество реально исполненных команд программы;
- количество реально исполненных команд программы; 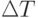 - интервал времени, регламентируемый соотношением дальности до цели и скоростями полета цели и зенитного снаряда;
- интервал времени, регламентируемый соотношением дальности до цели и скоростями полета цели и зенитного снаряда; 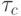 - скорость выполнения арифметико-логических действий используемым вычислителем.
- скорость выполнения арифметико-логических действий используемым вычислителем.
На рубеже XX века Давид Гильберт сформулировал задачу "автоматизации" процесса вывода математических теорем: "Можно ли построить алгоритм, строящий необходимый алгоритм решения любой точно поставленной задачи?". Программа Д. Гильберта была направлена на получение универсального алгоритма, сводившего деятельность математиков к формальной механической игре, в которой произвольную формализованную задачу (точно описанную на языке математики) можно было решить механически,используя процедуры универсального алгоритма. Парадокс программы Д. Гильберта обнаружился практически сразу [3] и состоит он в том, что для доказательства существования такого универсального алгоритма требуется его строгое математическое описание. Этот парадокс был обнаружен Бертраном Расселом (впоследствии научный руководитель Н. Винера в аспирантуре) и сводился к хорошо известному еще древним грекам парадоксу брадобрея, "который бреет всех тех и только тех мужчин деревни, которые не бреются сами". Вопрос "Кто бреет брадобрея?" ставит любую "формальную" машину в тупик, так как такой брадобрей существует в том и только в том случае, когда его нет. Аналогичная ситуация складывается и с "множеством всевозможных подмножеств, которые не включают себя в качестве элемента", что является необходимым условием существования универсального алгоритма Гильберта.
Чтобы обойти возникшую парадоксальную ситуацию, было предложено большое количество уточнений понятия алгоритма, а наш соотечественник академик Андрей Николаевич Колмогоров построил схему, лежащую в основе любого уточнения этого понятия. С помощью этой схемы можно строить новые уточнения как угодно долго.
В вычислительной технике остановились на уточнении понятия алгоритма, которое предложил английский математик Алан Матис Тьюринг и которое известно под названием "машина Тьюринга". Эта "машина" до сих пор служит формально-логическим прототипом любой ЭВМ. Машина Тьюринга состоит из [4]:
- разделенной на клетки бесконечной ленты;
- управляющего устройства, способного перемещаться вдоль ленты и выполнять предписанные "элементарные" действия;
- специальной таблицы управления, задающей правила функционирования всей машины.
На ленту можно записывать "слова", то есть упорядоченные последовательности символов из некоторого фиксированного и конечного алфавита.
На каждом шаге своей работы устройство управления извлекает символ, стоящий в клетке, против которой находится курсор устройства управления. Прочитав символ, устройство управления анализирует состояние, в котором оно находится в данный момент времени или, что одно и тоже, на данном такте работы. Список возможных состояний устройства управления конечен, фиксирован и известен заранее, а пара "считанный символ - состояние устройства управления" однозначно идентифицирует каждую клетку таблицы управления, на основе которой и определяется реакция машины Тьюринга. Считанный символ обычно идентифицирует строку, а состояние - столбец таблицы управления. В идентифицированной таким образом клетке таблицы управления записана инструкция, которую и должна выполнить машина Тьюринга.
Каждая инструкция в явном виде содержит:
- какой символ надо записать на место считанного символа;
- состояние, в которое должно перейти устройство управления;
- указание на направление перемещения по ленте: "вправо" или "влево".
Выполнив все указания, содержащиеся в данной клетке таблицы управления, машина Тьюринга завершает один цикл своей работы. Пусть машина Тьюринга работает по правилам табл. 1.1 [4].
Здесь символ "  " соответствует "пустой" клетке бесконечной ленты машины. "Слова", которые понимает данная машина Тьюринга, не должны содержать подряд несколько символов "
" соответствует "пустой" клетке бесконечной ленты машины. "Слова", которые понимает данная машина Тьюринга, не должны содержать подряд несколько символов " 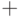 ", и этот символ не может находиться в начале и в конце "слова", то есть запрещенными считаются последовательности вида:
", и этот символ не может находиться в начале и в конце "слова", то есть запрещенными считаются последовательности вида: 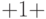 ,
, 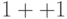 и т. п., а разрешенными считаются последовательности вида:
и т. п., а разрешенными считаются последовательности вида: 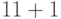 и т. п.
и т. п.
Состояние 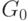 является начальным. Оно бесконечно долго сохраняет неизменными все символы на ленте и себя, то есть устройство управления не смещается вправо. Два других состояния являются рабочими, а обрабатываемые "слова" располагаются справа от курсора устройства управления.
является начальным. Оно бесконечно долго сохраняет неизменными все символы на ленте и себя, то есть устройство управления не смещается вправо. Два других состояния являются рабочими, а обрабатываемые "слова" располагаются справа от курсора устройства управления.
Пусть на бесконечной ленте такой машины Тьюринга записана последовательность символов 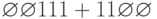 , а место положения курсора отмечено состоянием
, а место положения курсора отмечено состоянием  , в которое переведена машина под принудительным внешним воздействием:
, в которое переведена машина под принудительным внешним воздействием:
Согласно данным таблицы управления 1 машина Тьюринга считывает символ  , записывает в освободившуюся клетку символ
, записывает в освободившуюся клетку символ  (сохраняет содержимое предыдущей клетки) и смещается вправо на одну позицию, сохранив состояние
(сохраняет содержимое предыдущей клетки) и смещается вправо на одну позицию, сохранив состояние  :
:
На втором шаге действия машины Тьюринга повторяются, так как ситуация аналогична первому шагу, что приводит к простому смещению по ленте устройства управления еще на один шаг вправо:
На третьем шаге машина Тьюринга переходит в состояние 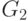 , в предыдущую клетку записывает символ "
, в предыдущую клетку записывает символ "  " и смещается по ленте еще на 1 шаг вправо:
" и смещается по ленте еще на 1 шаг вправо:
На четвертом шаге машина Тьюринга сохраняет свое состояние, содержимое четвертой клетки ленты и смещается вправо на 1 шаг:
Пятый шаг аналогичен четвертому и машина Тьюринга оказывается в положении:
На шестом шаге машина Тьюринга подставляет символ "  " вместо символа "
" вместо символа " 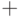 ", переходит в состояние
", переходит в состояние 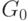 и смещается вправо на 1 шаг:
и смещается вправо на 1 шаг:
Такое положение соответствуют элементарной операции Stop, которая останавливает работу машины Тьюринга, когда на ленте сформирована последовательность символов, отвечающая операции сложения двух входных "слов":  и
и  .
.
Отсюда, машина Тьюринга оказалась "формальным" прототипом всех реальных ЭВМ, благодаря тому что содержала все базовые функциональные "блоки", в том числе и современных процессоров и ЭВМ:
- "операционное устройство", которое выполняет подстановку (замещение) символов на бесконечной ленте, используемой как память данных;
- устройство микропрограммного управления на основе постоянного запоминающего устройства (ПЗУ) команд, которое хранит таблицу управления.
При этом память программ и данных совмещена на бесконечной ленте, а инструкции и данные отличаются только набором символов.
Как и любую современную ЭВМ, машину Тьюринга можно вывести из начального состояния ( активизировать ) только принудительным внешним воздействием.
Главное отличие машины Тьюринга от реальных ЭВМ - это бесконечная память, которая позволяет обходиться в "программах" без операторов переходов по условию и по счетчику циклов, то есть неотъемлемым атрибутом ограниченной памяти реальных ЭВМ являются языковые средства организации циклов, которые способны при сбоях сделать программу обработки "бесконечной" ("зависание ЭВМ").
Но разработчикам первых ЭВМ пришлось ограничить набор символов машины Тьюринга и перейти к двоичному алфавиту, сначала при кодировании потоков данных, а впоследствии и потоков инструкций. При этом удалось сохранить главную "механическую" особенность машины Тьюринга: она не выполняет арифметико-логические действия, а осуществляет операции подстановки (замещения) символов, которые только при определенных условиях отвечают арифметическим действиям над числами.
В литературе нет точных указаний на автора, предложившего совместить в реальной ЭВМ принципы и методы организации вычислений машины Тьюринга с операционным базисом булевой алгебры и вытекающей из нее двоичной арифметики. Можно только предположить, что наработанные к тому времени в телефонии методы и средства описания работы релейных схем в операционном базисе булевой алгебры сыграли в этом не последнюю роль, так как они позволили создать высокоскоростные электротехнические средства управления телефонными коммутаторами, заменившими труд телефонисток. Поэтому разработчикам первых ЭВМ оставалось только создать электронный эквивалент переключательных схем и на их основе синтезировать "высокопроизводительное" по меркам того времени операционное устройство, работающее в булевом операционном базисе.
Технические предпосылки для перехода к электронным переключательным схемам сформировались в радиотехнике, успешно освоившей к тому времени методы и средства управления потоками электронов (током) в электронных лампах усилительных устройств приемников и передатчиков. В результате современникам Н. Винера осталось сделать только один, но решающий шаг, и заставить электронные лампы работать в "сверхбыстром" по отношению к реле переключательном режиме "насыщения" (булева "единица") и "отсечки" (булев "ноль"). Именно этот шаг и позволил объединить принципы и методы организации вычислений А. Тьюринга (в современной терминологии - системотехнический уровень организации вычислений) с физико-техническими процессами, отвечающими требованиям алгебры Дж. Буля (в современной терминологии - схемотехнический уровень организации вычислений).
Сама булева алгебра также появилась не на пустом месте и решала задачи символьной логики, восходящей своими корнями к логике Аристотеля, который сформулировал правила, регламентирующие споры схоластов и делающие эти споры конечными во времени.
До нас законы формальной логики Аристотеля дошли в виде трех аксиом и одного правила вывода [5]:
Первая аксиома позволяет заменить классы однотипных (тождественных, неразличимых и т. п.) высказываний символами (переменными). Вторая аксиома ограничивает пространство значений логических переменных двумя значениями: "ноль" (ложь) и "единица" (истина). Третья аксиома и правило вывода говорят о том, что отдельные высказывания всегда находятся в определенной связи друг с другом, количество которых ограничено:  ;
; 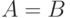 ; или
; или 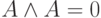 ;
; 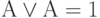 ;
; 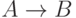 , то есть в формальной логике всегда существует два типа символов: для обозначения переменных и для обозначения связанных действий над переменными.
, то есть в формальной логике всегда существует два типа символов: для обозначения переменных и для обозначения связанных действий над переменными.
Логика Аристотеля дедуктивная и поэтому она позволяет судить об истинности или ложности частных высказываний на основании истинности или ложности общих высказываний (аксиом), служащих им основанием. Например [4]:
- Все люди смертны.
- Гай Юлий Цезарь - человек.
- Гай Юлий Цезарь - смертен.
Следует иметь в виду, что формальная логика имеет достаточно ограниченную область применения и поэтому ее правила и законы не следует абсолютизировать. Например, согласно Аристотелевой логике правомерна конструкция:
- Редкая птица долетит до середины Днепра.
- Пингвин - редкая птица.
- Значит, пингвин долетит до середины Днепра.
Отсюда, жизнь требует перехода не только от осмысленных (содержательных) высказываний к представляющим их формальным высказываниям и переменным, но и наоборот. Выработкой правил такого перехода занималась наука герменевтика [4], которая играла важную роль в теологии. В переводе с греческого герменевтика - это трактование понятий, толмачество, то есть перевод с непонятного языка на понятный. Толмачи выступают как интерпретаторы,разъясняющие, что хотел сказать автор, например Гомер своим читателям. Поэтому в процессе разъяснений толмач прибегал к аналогиям:
- Трамвай - общественный транспорт.
- Автобус - общественный транспорт.
- Трамвай перевозит пассажиров.
- Следовательно, автобус также перевозит пассажиров.
Вывод по аналогии, как и всякий индуктивный вывод, не всегда приводит к правильному результату:
- Агата Кристи - писатель.
- Теодор Драйзер - писатель.
- Агата Кристи пишет детективы.
- Следовательно, Теодор Драйзер также пишет детективы.
Первую конструкцию рассуждений можно воспроизвести в Аристотелевой логике, построив более общее высказывание: "Общественный транспорт перевозит пассажиров". Во второй конструкции это сделать не удается. Поэтому, чтобы решить задачу интерпретации результатов доказательств и рассуждений дедуктивным методом и однозначно,необходимо ввести определенные ограничения на правила или схему интерпретации, которые выработала герменевтика,занимаясь трактованием богословских текстов. Согласно этой схеме сначала выбирается совокупность утверждений, истинность которых признана большинством людей. Они служат базисом для вывода других утверждений, а сам вывод из базисных утверждений подчинен определенным правилам. Например:
Каждый человек стремится получить удовольствие.
Из двух зол каждый человек выбирает меньшее.
Поэтому если кандидат  на выборах (президента, мэра, парламента и т. п.) меньшее зло, чем кандидат
на выборах (президента, мэра, парламента и т. п.) меньшее зло, чем кандидат  , то на выборах победит кандидат
, то на выборах победит кандидат  .
.
В современной терминологии совокупность правил "трактования" результатов вычислений задается протоколами работы интерфейсов и средств коммутации, как самих ЭВМ, так и многомашинных комплексов, сетей и систем.
Дж. Буль, решая задачи символической логики, предложил отказаться от смыслового содержания высказываний и выработал правила логического вывода, допустив, что каждое высказывание может быть либо истинным, либо ложным, а представляющие его логические переменные могут принимать значение либо "ноль", либо "единица". В этом случае действия, связующие переменные, можно ограничить тремя, которые обладают базисным свойством: 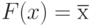 - инверсия;
- инверсия; 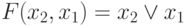 - дизъюнкция и
- дизъюнкция и 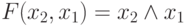 - конъюнкция, которые в обиходе назы-ваются, соответственно, "ОТРИЦАНИЕ", "ИЛИ" и "И". В математике и логике базисными считаются функции, через суперпозицию которых можно представить любые другие функции из некоторого фиксированного класса. Поэтому для того, чтобы покрыть все многообразие функциональных блоков системотехнического уровня организации вычислений, разработчикам первых ЭВМ требовалось реализовать на физико-техническом уровне только три типа переключательных функций, заданных таблицами истинности:
- конъюнкция, которые в обиходе назы-ваются, соответственно, "ОТРИЦАНИЕ", "ИЛИ" и "И". В математике и логике базисными считаются функции, через суперпозицию которых можно представить любые другие функции из некоторого фиксированного класса. Поэтому для того, чтобы покрыть все многообразие функциональных блоков системотехнического уровня организации вычислений, разработчикам первых ЭВМ требовалось реализовать на физико-техническом уровне только три типа переключательных функций, заданных таблицами истинности:
Для этого были использованы электронные лампы, которые в радиотехнических устройствах работали в усилительном, а не переключательном режиме. С помощью таких ламп было синтезировано электронное вычислительное устройство, которое представляло собой расширенный аналог электромеханического арифмометра, так как содержало оперативную память объемом несколько десятков килобит и электромеханическое устройство микропрограммного управления на основе телетайпа с закольцованной перфолентой, где и хранилась микропрограмма выполнения умножения или деления.
Однако решение в реальном времени задачи экстраполяции случайной траектории полета самолета требовало автоматизации управления не только отдельными командами, но и их потоками, которые определяются как программами обработки, так и содержимым обрабатываемых потоков данных. Последнее условие делает поток команд частично упорядоченным во времени и обусловлено необходимостью организации циклов при работе с конечной, а не с бесконечной памятью, как это имеет место в машине Тьюринга. Поэтому основным препятствием на пути достижения потребной производительности, диктуемой задачами экстраполяции случайной траектории полета самолета, стало медленное устройство управления, неспособное управлять частично упорядоченными во времени потоками инструкции. Чтобы преодолеть это препятствие и выравнять скорости обработки и управления вычислениями, Дж. фон Нейман предложил использовать электронную память не только для хранения данных, но и для хранения программ. Такое решение потребовало двоичного кодирования не только да нных, но и команд, что привело к дуализму (кодовой неразличимости) потоков инструкций и данных, который сохранился во всех последующих поколениях ЭВМ вплоть до наших дней. В итоге архитектура фон-неймановской ЭВМ приняла вид как на рис. 1.1, где все электронные устройства обмениваются информацией через общую электронную шину.
Основные достоинства фон-неймановской архитектуры:
- потоки команд и данных сбалансированы по скорости инициализации и обработки;
- расширение функциональных возможностей ЭВМ осуществляется стандартным протоколом подключения к общей шине.
- разделить память команд и данных можно только конструктивно, что приводит к необходимости использования системных программно-аппаратных средств защиты этих разделов памяти;
- централизованный коммутационный ресурс в виде общей шины снижает пропускную способность как по wпотокам команд и данных из-за блокировок коммутации и издержки блокировок тем выше, чем больше устройств ЭВМ обслуживает одна шина.
Таким образом, общая систематика, предопределившая появление, а в дальнейшем и развитие ЭВМ, их архитектур и вычислительных технологий в целом сводится к следующему (рис. 1.2).
- Постоянным источником зарождения и развития средств вычислительной техники была и остается диспропорция между предоставляемой и потребной производительностью, первая из которых определяется уровнем развития производства аппаратуры, а вторая - спектром решаемых задач с экстремальными характеристиками. Лидирующее положение среди таких задач занимают задачи, направленные на устранение или хотя бы ослабление глобальных или локальных, реальных или потенциальных угроз в военной области, экологии, экономике, социальной сфере и т. д.
- Качественный скачок в вычислительной технике всегда обусловлен комплексом формально-логических, системотехнических, схемотехнических и физико-технических предпосылок, обеспечивающих переход к новым вычислительным технологиям и программно-аппаратным платформам их поддержки.
- Сбалансированность скоростей передачи и обработки потоков команд и данных была и остается необходимым условием повышения эффективности использования физических возможностей ЭВМ. Именно сбалансированность фон-неймановских ЭВМ по скоростям потоков команд и данных повысила их производительность до 20 тыс. операций в секунду, что оказалось достаточным для решения в реальном времени задач экстраполяции случайных траекторий полета самолетов.
- Парирование угрозы, связанной с колоссальными потерями среди мирного населения, привело к качественному скачку на 5-6 порядков в производительности средств вычислительной техники, чего не знала и пока не знает история развития человечества. Сам скачок был обусловлен междисциплинарным подходом к прорывному исследовательскому проекту в области вычислительной техники, что в современных условиях является необходимым признаком инновации.
- Центральная проблема повышения эффективности использования средств вычислительной техники - это улучшение качества управления операционным, коммутационным ресурсом и ресурсами памяти, а значит и потоками инструкций и данных.


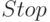
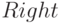
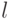 ,
,