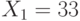| Россия, Москва, МЭИ, 2006 |
Междисциплинарный характер компьютерных проектов
1.6. Обобщенная схема организации вычислений
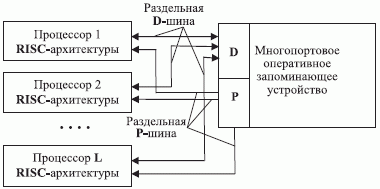
В машине Тьюринга можно выделить два уровня управления, один из которых связан с исполнением текущей инструкции "программы", а другой - с инициализацией самой инструкции или "чтением" самой программы, то есть с перемещением управляющего устройства по ленте. В реальных ЭВМ перемещение курсора машины Тьюринга заменено смещением указателя адреса по разделу памяти программ ( P- область ОЗУ) конечного объема. Аналогично и для перемещения по таблице управления устройства управления машины Тьюринга, которое в процессорах с микропрограммным управлением заменено модификацией адреса в постоянном запоминающем устройстве микропроцессора. Поэтому общая процедура выполнения инструкций программы имеет вид: "Делай то, что расположено по указателю адреса … в P- области ОЗУ над тем, что расположено по указателю адреса … в D- области ОЗУ" (рис. 1.13).
В результате идентификатор программы представляет собой указатель адреса первой инструкции этой программы, а считанный по этому адресу код операции представляет собой адрес микропрограммы, исполняющей эту ассемблерную инструкцию. Отсюда, вычислительный процесс представляет собой два процесса: перечисления потоков инструкций и данных и преобразования потоков инструкций и данных, причем потоки и инструкций, и данных неразличимы в кодовом представлении.
Перечислительная составляющая представляет собой частично упорядоченный поток адресов инструкций и данных, что обусловлено конечным объемом памяти. Вычислительная составляющая представляет собой последовательность микрокоманд, которые осуществляют булевы преобразования двоичных переменных, и требуются специальные меры, чтобы эти преобразования были адекватны арифметическим действиям над двоичными переменными.
Поэтому правильнее говорить, что вычислительная машина не вычисляет, а преобразует коды инструкций и данных. Чтобы убедиться в этом, достаточно вспомнить, что:
- символ (цифра) обозначает предмет или явление;
- число или упорядоченная последовательность символов выражает количественные соотношения между предметами или явлениями;
- код представляет упорядоченные последовательности символов.
Например, двоичная последовательность 1011 в ЭВМ может интерпретироваться:
- как код операции по 13 адресу ПЗУ микропрограмм;
- как целое число 13 без знака;
- как отрицательное целое число -3;
- как отрицательное дробное число -0,375, и т. п.
Но система преобразований булевой алгебры ЭВМ выбрана таким образом, чтобы выполненные над двоичной последовательностью инструкции не зависели от правил интерпретации переменных на входе и выходе ЭВМ. По этой причине даже знаковые разряды чисел "складываются" в дополнительных кодах по правилам значащих разрядов: число - 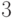 в дополнительном коде -
в дополнительном коде - 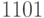 , а число -2 в дополнительном коде -
, а число -2 в дополнительном коде -  . Поэтому сложение кодов этих чисел в двоичной системе счисления имеет вид:
. Поэтому сложение кодов этих чисел в двоичной системе счисления имеет вид:
а результат  представляет в дополнительном коде число -5, для получения которого необходимо перейти на выходе ЭВМ к прямому коду
представляет в дополнительном коде число -5, для получения которого необходимо перейти на выходе ЭВМ к прямому коду 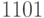 , то есть чтобы правильно интерпретировать на выходе ЭВМ результат сложения двух отрицательных чисел, их сумму необходимо перевести в прямой код. Система булевых преобразований однобитного сумматора имеет вид:
, то есть чтобы правильно интерпретировать на выходе ЭВМ результат сложения двух отрицательных чисел, их сумму необходимо перевести в прямой код. Система булевых преобразований однобитного сумматора имеет вид:
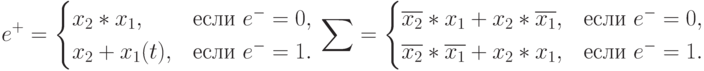
Здесь 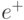 ,
, 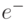 и
и  - соответственно "единица переноса" в последующий разряд, "единица переноса" предыдущего разряда и "сумма" текущего разряда, а
- соответственно "единица переноса" в последующий разряд, "единица переноса" предыдущего разряда и "сумма" текущего разряда, а  ,
, 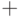 и
и  - соответственно булева операция "И", "ИЛИ" и "ОТРИЦАНИЕ".
- соответственно булева операция "И", "ИЛИ" и "ОТРИЦАНИЕ".
Таким образом, входные данные ЭВМ сначала представляются в двоичном коде, далее над ними выполняются булевы преобразования,результаты которых интерпретируются ("трактуются") на выходе ЭВМ.
Следует иметь в виду, что правила интерпретации двоичных кодов чисел на входе ЭВМ существенно изменяют и систему преобразований булевых функций в самой ЭВМ. В нашем примере подразумевалась классическая позиционная система счисления, в которой "вес"  -го разряда для целых чисел определяется по правилу:
-го разряда для целых чисел определяется по правилу: 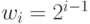 .
Однако это не единственная позиционная система счисления; для сравнения рассмотрим числа Фибоначчи и отвечающие им правила выполнения арифметических действий [37].
.
Однако это не единственная позиционная система счисления; для сравнения рассмотрим числа Фибоначчи и отвечающие им правила выполнения арифметических действий [37].
Последовательность чисел Фибоначчи появились в 1202 году из задачи о размножении кроликов. Пара кроликов каждый месяц приносит приплод из двух крольчат: самки и самца. Период созревания крольчат составляет 2 месяца, и они начинают размножаться по тому же правилу.
Задача: определить количество пар кроликов через 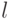 месяцев, если размножение началось с 1-й пары зрелых кроликов и если оно началось с пары новорожденных кроликов.
месяцев, если размножение началось с 1-й пары зрелых кроликов и если оно началось с пары новорожденных кроликов.
Обозначим через 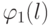 количество пар кроликов по истечении l месяцев с начала размножения (
количество пар кроликов по истечении l месяцев с начала размножения ( 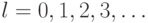 ). Тогда при
). Тогда при 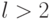 количество пар кроликов можно определить по рекуррентному соотношению:
количество пар кроликов можно определить по рекуррентному соотношению: 
В этом соотношении начальные условия зависят от "зрелости" кроликов в начале размножения:
-
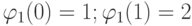 - для зрелой пары,
- для зрелой пары, -
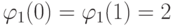 - для незрелой пары.
- для незрелой пары.
Тогда последовательности чисел Фибоначчи запишутся:
- а)
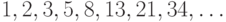 - для зрелой пары,
- для зрелой пары, - б)
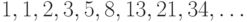 - для незрелой пары, то есть эти последовательности разнятся только на первом шаге.
- для незрелой пары, то есть эти последовательности разнятся только на первом шаге.
Обобщенные числа Фибоначчи 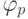 учитывают разные периоды (
учитывают разные периоды (  ) созревания молодых пар и разные коэффициенты размножения.
) созревания молодых пар и разные коэффициенты размножения.
Связь чисел Фибоначчи с последовательностью двоичных "весовых" коэффициентов достаточно проста и определяется условием "мгновенного" созревания молодых пар  . Тогда
. Тогда 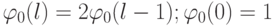 и поэтому
и поэтому 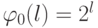 , то есть последовательность "весовых" коэффициентов класси-ческой позиционной двоичной системы счисления:
, то есть последовательность "весовых" коэффициентов класси-ческой позиционной двоичной системы счисления: 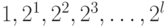 .
.
Если 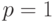 , то получим классический ряд чисел Фибоначчи, а если
, то получим классический ряд чисел Фибоначчи, а если 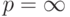 , то есть процесс созревания молодой пары кроликов приобрел бесконечный характер, то в случае взрослой пары только она и размножается:
, то есть процесс созревания молодой пары кроликов приобрел бесконечный характер, то в случае взрослой пары только она и размножается:  , а в случае новорожденной пары
, а в случае новорожденной пары 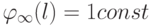 .
.
Как и в любой позиционной системе счисления, представление деся
тичных чисел в базисе Фибоначчи имеет вид  , но
, но 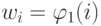 , а не
, а не 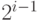 :
:
В нашем примере 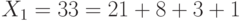 , а
, а 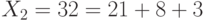 .
.
В системе Фибоначчи число считается нормализованным, если в нем нет смежных "единичных разрядов". Например, число  считается ненормализованным, так как в его правых, младших разрядах подряд стоят две "единицы", которые можно заменить одной "единицей" в ближайшем, старшем разряде:
считается ненормализованным, так как в его правых, младших разрядах подряд стоят две "единицы", которые можно заменить одной "единицей" в ближайшем, старшем разряде: 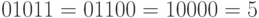 .
.
В арифметике Фибоначчи арифметические действия выполняются только над нормализованными числами. В частности, сложение выполняется по следующей схеме:
Здесь "единица переноса" "раздваивается" и, как обычно, учитывается при суммировании старшего разряда, а также размещается со сдвигом на 2 разряда в частной единице переноса 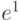 .
.
Полученная частная сумма 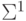 и частная "единица переноса"
и частная "единица переноса" 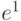 имеют нормализованное представление, поэтому на втором шаге их можно сложить:
имеют нормализованное представление, поэтому на втором шаге их можно сложить:
Результат суммирования получился ненормализованным и его надо привести к нормализованному виду. Нормализация проводится начиная со старшей группы разрядов, где стоят подряд как минимум две "единицы":
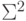 |
0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
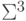 |
0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
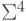 |
0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
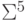 |
0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
 |
89 | 55 | 34 | 21 | 13 | 8 | 5 | 3 | 2 | 1 | 1 |
Нормализованный результат имеет вид: 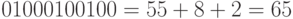 , и его можно использовать в дальнейших вычислениях.
, и его можно использовать в дальнейших вычислениях.
Отсюда, система булевых преобразований в одноразрядном сумматоре Фибоначчи имеет вид:  . и
. и 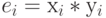 .
.
Таким образом, аппаратные затраты сумматора Фибоначчи гораздо меньше классического "булевого" сумматора, но процедура суммирования чисел Фибоначчи носит итеративный характер и требует циклической процедуры нормализации промежуточных операндов. Представление чисел в системе Фибоначчи требует большей разрядной сетки, чем классическое булево представление, так как "вес" разряда в последнем случае нарастает по самому быстрому экспоненциальному закону. Однако такую избыточность можно использовать для повышения обнаружения ошибок арифметических действий и повышения отказоустойчивости ЭВМ Фибоначчи [37].