| Россия, Москва, МЭИ, 2006 |
Нейрофизиологический и формально-логический базис нейроподобных вычислений
4.3. Формальная модель нейрона и сети Мак-Каллока - Питтса
Одна из первых успешных попыток построения формальной модели реальных нейронов была предпринята в 1943 году физиологом У.С. Мак-Каллоком и математиком У. Питтсом [64]. Главное ее достоинство - это простота, которая, с одной стороны, позволяет проводить анализ функциональных возможностей сложных нейронных структур, что важно для нейрофизиологов, а с другой стороны - оценивать функциональную устойчивость нейроподобных вычислительных структур при флуктуациях порогов, что важно для инженеров.
В дальнейшем под формальным нейроном стали понимать элемент вычислительной машины, который обладает следующими свойствами [65]:
- Элемент имеет
 нервных входных волокон и одно выходное волокно (аксон).
нервных входных волокон и одно выходное волокно (аксон). - Каждый вход и единственный выход могут находиться только в двух состояниях: "возбужден" или "не возбужден".
- Нервные волокна от некоторого входа могут разветвляться, но не могут объединяться с волокнами другого входа.
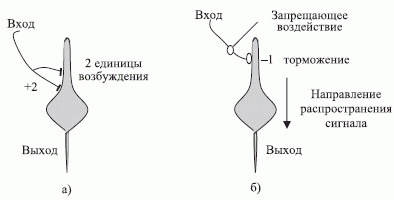
- Волокна могут быть возбуждающими (+1) или тормозящими (-1) (рис. 4.7-а). Волокно может также запирать сигнал, идущий по другому волокну (рис. 4.7-б).
- Через нейрон и по нервным волокнам сигналы распространяются только в одном направлении.
- В формальном нейроне имеется конечная задержка на распространение сигнала от входа к выходу.
- При правильной работе нейрон возбуждается, если алгебраическая сумма возбуждающих и тормозящих сигналов превосходит некоторый фиксированный порог ?.
Фактически У. Мак-Каллоку и У. Питтсу удалось корректно формализовать известные на тот момент времени механизмы синаптической передачи электрофизиологических возбуждений (см. раздел 4.1).
Для описания логических функций, реализуемых формальным нейроном, используют диаграммы Венна, в которых логические переменные представлены следующими областями (рис. 4.8):
Для изображения логических функций с помощью диаграмм Венна достаточно поставить точку в соответствующем месте:
Вид реализуемой формальным нейроном логической функции зависит как от правил соединения волокон, так и от значения порога. Если формальный нейрон имеет  входов, то множество возможных комбинаций значений входных сигналов насчитывает
входов, то множество возможных комбинаций значений входных сигналов насчитывает 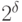 значений, которым на диаграмме Венна соответствует своя область. Поэтому каждой комбинации значений входных сигналов можно поставить в соответствие суммарное значение возбуждения, которое можно представить числом и записать его в соответствующую область диаграммы Венна. В результате каждый формальный нейрон
рис. 4.9 можно представить эквивалентным нейроном
рис. 4.10.
значений, которым на диаграмме Венна соответствует своя область. Поэтому каждой комбинации значений входных сигналов можно поставить в соответствие суммарное значение возбуждения, которое можно представить числом и записать его в соответствующую область диаграммы Венна. В результате каждый формальный нейрон
рис. 4.9 можно представить эквивалентным нейроном
рис. 4.10.
![В каждой области диаграммы Венна указана величина возбуждения при соответствующей входной комбинации [65]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_10.gif)
Рис. 4.10. В каждой области диаграммы Венна указана величина возбуждения при соответствующей входной комбинации [65]
Возможен и другой вариант представления формального нейрона, когда в поля диаграммы Венна вписаны числа, отвечающие порядку появления соответствующей точки при возрастании порога исходного нейрона (рис. 4.11).
![В каждой области диаграммы Венна указано число, соответствующее порядку появления точек при возрастании порога [65]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_11.gif)
Рис. 4.11. В каждой области диаграммы Венна указано число, соответствующее порядку появления точек при возрастании порога [65]
Сетью Мак-Каллока называется объединение четырех или более рядов формальных нейронов без обратных связей типа рис. 4.12.
Из приведенных данных следует:
- одна и та же логическая функция (в данном случае это
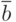 ) может быть реализована как одиночным формальным нейроном, так и сетью, элементы которой настроены на более "сложные" логические функции, то есть между "сложностью" функции и "сложностью" реализующей ее структуры нет и не может быть взаимно однозначного соответствия (структурно-функциональный полиморфизм);
) может быть реализована как одиночным формальным нейроном, так и сетью, элементы которой настроены на более "сложные" логические функции, то есть между "сложностью" функции и "сложностью" реализующей ее структуры нет и не может быть взаимно однозначного соответствия (структурно-функциональный полиморфизм); - формальный нейрон является функционально полным в том смысле, что его можно настроить на реализацию любой логической функции, в данном случае двух переменных.
При этом следует иметь в виду, что полнота формального нейрона достигается за счет его структурно-параметрической перестройки, то есть вариацией порога как параметра и схемы соединения с другими нейронами сети как структурного фактора.
Чтобы по известной структуре сети определить реакцию выхода, необходимо руководствоваться следующими правилами:
- Выходное преобразование нейрона первого ряда всегда совпадает с его логической функцией.
- Выходное преобразование нейрона второго (и последующего) ряда определяется в следующей последовательности:
- На диаграмме Венна одного из нейронов второго ряда рассматривается область, отвечающая
 . Если в этом месте имеется точка,следует рассмотреть выходные диаграммы Венна нейронов первого ряда и найти среди них все общие множества, в которых и в левой, и в правой диаграммах имеются точки. Затем в выходной диаграмме Венна рассматриваемого нейрона второго ряда надо поставить точку (точки) в области (областях), соответствующих каждому общему множеству. (В схеме
рис. 4.12 левый нейрон имеет точку в области
. Если в этом месте имеется точка,следует рассмотреть выходные диаграммы Венна нейронов первого ряда и найти среди них все общие множества, в которых и в левой, и в правой диаграммах имеются точки. Затем в выходной диаграмме Венна рассматриваемого нейрона второго ряда надо поставить точку (точки) в области (областях), соответствующих каждому общему множеству. (В схеме
рис. 4.12 левый нейрон имеет точку в области  и оба нейрона первого слоя имеют общую точку в области
и оба нейрона первого слоя имеют общую точку в области  , что и соответствует его выходной реакции.)
, что и соответствует его выходной реакции.) - Если в области
 точка отсутствует, то анализируется область
точка отсутствует, то анализируется область  для всех нейронов второго ряда (движение против часовой стрелки по диаграмме Венна). Если такая точка имеется (в нашем случае это правый нейрон), то в диаграммах Венна нейронов первого ряда необходимо найти все общие множества, в которых в левой диаграмме имеется точка, а в правой отсутствует. В нашем случае данному условию удовлетворяет область
для всех нейронов второго ряда (движение против часовой стрелки по диаграмме Венна). Если такая точка имеется (в нашем случае это правый нейрон), то в диаграммах Венна нейронов первого ряда необходимо найти все общие множества, в которых в левой диаграмме имеется точка, а в правой отсутствует. В нашем случае данному условию удовлетворяет область  левого и правого нейрона первого ряда, что порождает точку в аналогичной области правого нейрона второго ряда.
левого и правого нейрона первого ряда, что порождает точку в аналогичной области правого нейрона второго ряда. - Аналогично определяется выходная реакция для остальных областей диаграммы Венна второго ряда с той разницей, что для области
 нейроны первого ряда не должны иметь точек в одинаковых областях, а для области
нейроны первого ряда не должны иметь точек в одинаковых областях, а для области  точка должна быть в правой выходной диаграмме и ее не должно быть в левой. В нашем случае области
точка должна быть в правой выходной диаграмме и ее не должно быть в левой. В нашем случае области  и
и  точек не имеют, и поэтому процедура определения выходных преобразований нейронов второго ряда завершена.
точек не имеют, и поэтому процедура определения выходных преобразований нейронов второго ряда завершена.
- На диаграмме Венна одного из нейронов второго ряда рассматривается область, отвечающая
Выходная реакция единственного нейрона третьего ряда, а значит, и всей сети определяется двумя точками собственной диаграммы Венна:
-
 , что требует наличия точки в левой диаграмме второго слоя и ее отсутствия в правой; такому условию отвечает область
, что требует наличия точки в левой диаграмме второго слоя и ее отсутствия в правой; такому условию отвечает область  нейронов второго слоя, и поэтому в выходную реакцию всей сети проставляется точка в эту же область;
нейронов второго слоя, и поэтому в выходную реакцию всей сети проставляется точка в эту же область; -
 , что требует наличия точки в правой диаграмме второго слоя и ее отсутствия в левой; такому условию отвечает область
, что требует наличия точки в правой диаграмме второго слоя и ее отсутствия в левой; такому условию отвечает область  нейронов второго слоя, и поэтому в выходную реакцию всей сети проставляется точка в эту же область.
нейронов второго слоя, и поэтому в выходную реакцию всей сети проставляется точка в эту же область.
Сети из формальных нейронов позволили перевести из абстрактной в инженерную плоскость исследования по синтезу надежных элементов из ненадежных компонент Дж. фон Неймана [66]. В частности, сеть рис. 4.13 логически устойчива при колебаниях порогов в пределах 75 %. (Сеть считается логически устойчивой, если она сохраняет реализуемую логическую функцию при одновременной флуктуации порогов составляющих формальных нейронов [65].)
В рамках этих исследований удалось показать [65]:
- Всегда можно построить логически устойчивую сеть, вычисляющую любую заданную функцию при колебаниях порогов у нейронов сети в пределах
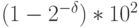 .
. - Если у всех составляющих сеть нейронов диаграммы Венна содержат одинаковое количество точек, то для
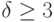 сеть сохраняет логическую устойчивость при флуктуациях порогов в пределах
сеть сохраняет логическую устойчивость при флуктуациях порогов в пределах 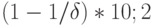 }.
}.
С.О. Мкртчян предложил схему формального нейрона с разрешающими взаимодействиями входных волокон [67], которые он привел к входам формального нейрона, дополнив пороговый элемент блоком входных логических преобразований (рис. 4.14 [68]), эквивалентных "сетевым преобразованиям" формального нейрона Мак-Каллока - Питтса.
При этом С.О. Мкртчян отказался от традиционного сетевого подхода к построению нейро-ЭВМ и сосредоточил свои усилия на синтезе традиционных блоков и устройств вычислительной техники на основе аппаратно реализованных формальных нейронов. В итоге были синтезированы все блоки и устройства традиционных ЭВМ, включая и конечные автоматы, основу которых составляют RS -триггеры (рис. 4.15).
увеличить изображение
Рис. 4.14. Формальные нейроны с равноправными запрещающими и разрешающими входами [68]
Тем не менее, нейрокомпьютерная и компьютерная техника продолжили развиваться параллельными курсами, что можно объяснить следующими причинами. Технологические успехи микроэлектроники выдвинули на первый план не минимизацию затрат активных (преобразующих) элементов (транзисторов), а средств коммутации, которые стали основными "пожирателями" площади кристаллов и главными источниками временных и энергетических издержек обмена информацией СБИС с "внешней средой". Более того, нейроподобная элементная база в принципе не могла выиграть у традиционных булевых вентилей даже по удельным аппаратным затратам, измеряемым количеством вентилей на одну реализуемую логическую функцию в составе многофункционального или универсального (функционально полного) логического модуля, на что, собственно, и делал ставку С.О. Мкртчян [68]. В частности, на универсальный логический модуль, реализующий 16 логических функций двух переменных, требуется всего 9 вентилей "И - НЕ " и два инвертора. В результате удельные затраты булевых вентилей на 1 логическую функцию составляют ~10 вентилей / 16 функций, то есть 0,625 вентиля на функцию. Для реализации в микроэлектронном операционном базисе порогового элемента на два входа требуются одноразрядный сумматор, блок сравнения и регистры хранения порога и весовых коэффициентов, где только на одноразрядный сумматор расходуется порядка 9 вентилей типа "И", "ИЛИ" и 4 инвертора. Поэтому нейроподобная элементная база способна выиграть у традиционных булевых вентилей только в том случае, если используемый физико-технический процесс будет адекватен системе преобразований формального нейрона "суммирование - сравнение - подстановка".
Этим можно объяснить возрождение интереса к нейросетевым вычислительным устройствам, которое произошло в середине 80-х годов прошлого столетия благодаря Дж. Хопфилду и Д. Танку [69], предложившим эффективную процедуру обучения сетей Мак-Каллока - Питтса. Именно эффективное обучение нейросетей пока является главным преимуществом нейрокомпьютерных технологий перед традиционными компьютерными технологиями, где главные временные издержки сосредоточены в процедурах формализации и программирования, с помощью которых задачи пользователя преобразуются в булево представление, исполняемое элементной базой ЭВМ.
Дж. Хопфилд и Д. Танк предложили проводить обучение нейро-ЭВМ на принципах аналоговой вычислительной техники, когда поиск решения дискретной задачи осуществляется в непрерывном пространстве, в котором как раз и выполняются нейронные вычисления. При этом обучение формулируется как поиск глобального оптимума некоторой функции, для достижения которого требуется как минимум умение выбираться из локального экстремума, для чего в аналоговые цепи обычно встраивают некоторые параметры "прибыли", которые эквивалентны параметру "температуры" в машине Больцмана.
Для этих целей подходит модель нейроподобной сети, в которой состояние  -го формального нейрона описывается выходом
-го формального нейрона описывается выходом  (излагается по [70]). Входные возбуждения формального нейрона формируются двумя источниками: внешним сигналом
(излагается по [70]). Входные возбуждения формального нейрона формируются двумя источниками: внешним сигналом 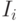 и состояниями осталь-ных нейронов. Дж. Хопфилд ввел энергетическую функцию произвольного состояния симметрично связанной сети:
и состояниями осталь-ных нейронов. Дж. Хопфилд ввел энергетическую функцию произвольного состояния симметрично связанной сети:
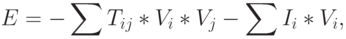 |
( 4.2) |
где первая сумма берется по 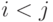 , вторая сумма просто по
, вторая сумма просто по  , а
, а 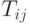 представляет силу синаптического взаимодействия нейрона
представляет силу синаптического взаимодействия нейрона 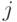 с нейроном
с нейроном 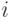 (в биологической интерпретации).
(в биологической интерпретации).
Из (4.2) следует, что в энергетическую функцию нейросети вклад вносят только возбужденные нейроны, у которых 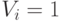 , что соответствует состоянию " on "
, что соответствует состоянию " on "  -го нейрона, а невозбужденные нейроны, у которых
-го нейрона, а невозбужденные нейроны, у которых 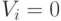 (состояние "off") никакого влияния на энергию всей сети не оказывают ни за счет первого, ни за счет второго слагаемого. Поэтому разность значений энергии
(состояние "off") никакого влияния на энергию всей сети не оказывают ни за счет первого, ни за счет второго слагаемого. Поэтому разность значений энергии  -го нейрона между его возбужденным и невозбужденным состояниями можно определить соотношением:
-го нейрона между его возбужденным и невозбужденным состояниями можно определить соотношением:
 |
( 4.3) |
Если 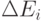 отрицательна, то для минимизации энергии требуется усиление взаимодействий этого нейрона с остальными и/или внешней средой. В противном случае требуется ослабление такого взаимодействия.
отрицательна, то для минимизации энергии требуется усиление взаимодействий этого нейрона с остальными и/или внешней средой. В противном случае требуется ослабление такого взаимодействия.
В такой интерпретации локальные и глобальные минимумы можно рассматривать в качестве хранимых образцов, а нейросеть - как структурно организованную ассоциативную память, устойчиво воспроизводящую совокупность минимумов, свойственных только данной нейросети ("хранящую" значения 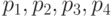 -
рис. 4.16).
-
рис. 4.16).
С другой стороны, используя модель отжига для выхода сети из локального минимума, можно для каждого  -го элемента памяти вычислить (4.3). Доказано, что двоичный механизм поиска глобального минимума регулируется вероятностной функцией
-го элемента памяти вычислить (4.3). Доказано, что двоичный механизм поиска глобального минимума регулируется вероятностной функцией 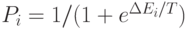 , где переменная
, где переменная 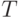 аналогична температуре в модельном отжиге и по существу является масштабирующим множителем, управляющим интенсивностью "шума", который поддерживает флуктуационный характер изменения энергии в сети. При возрастании
аналогична температуре в модельном отжиге и по существу является масштабирующим множителем, управляющим интенсивностью "шума", который поддерживает флуктуационный характер изменения энергии в сети. При возрастании 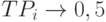 , и поэтому система ведет себя хаотично безотносительно к ограничениям в самой сети. При
, и поэтому система ведет себя хаотично безотносительно к ограничениям в самой сети. При 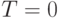 и
и 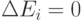 система становится детерминированной (
система становится детерминированной ( 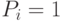 ) и скатывается в ближайший локальный минимум. Когда сеть Хопфилда - Танка достигает температурного равновесия, относительная вероятность ее нахождения в состоянии
) и скатывается в ближайший локальный минимум. Когда сеть Хопфилда - Танка достигает температурного равновесия, относительная вероятность ее нахождения в состоянии  по сравнению с вероятностью состояния
по сравнению с вероятностью состояния  в данный момент времени
в данный момент времени  подчиняется распределению Больцмана:
подчиняется распределению Больцмана: 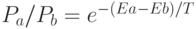 .
.
Отсюда, состояние температурного равновесия не гарантирует достижения некоторого устойчивого состояния в сети, причем сами состояния продолжают варьировать даже при установившемся распределении вероятностей.
Наилучшая стратегия достижения температурного равновесия (признак конца обучения нейросети) при любой заданной температуре 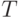 состоит в том, чтобы стартовать с высокой температуры, сделав легко преодолимыми энергетические барьеры системы, и постепенно понижать
состоит в том, чтобы стартовать с высокой температуры, сделав легко преодолимыми энергетические барьеры системы, и постепенно понижать  , повышая статус состояний с низкой энергией. В итоге при плавном
, повышая статус состояний с низкой энергией. В итоге при плавном
изменении температуры 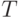 можно с большой вероятностью попасть в глобальный минимум или остановиться в достаточной близости от него. Таким образом, на основе приведенных данных можно заключить:
можно с большой вероятностью попасть в глобальный минимум или остановиться в достаточной близости от него. Таким образом, на основе приведенных данных можно заключить:
- Несмотря на свою простоту, сети Мак-Каллока - Питтса достаточно удобны как для моделирования "случайных" процессов, протекающих в реальной нервной системе, так и для эффективного определения структуры "дочерней" нейросети и ее параметров (порогов), что является итого обучения.
- В сетях Хопфилда - Танка структурно-параметрические методы хранения информации используются на уровне не субнейрональных, а межнейрональных взаимодействий, когда хранимые нейросетью данные воспроизводятся при переходе в одно из устойчивых состояний после ее возбуждения.
- Главным препятствием на пути эффективного использования ней-роподобных компьютерных технологий является неадекватность физико-технических процессов (суб)микронной микроэлектроники, ориентированных на переключательный характер булевого операционного базиса и неадекватных системам пороговых преобразований, лежащих в основе формальных нейронов.


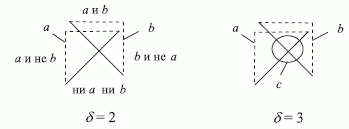
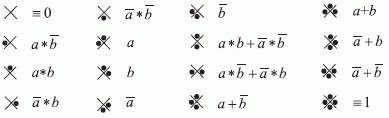
![Формальные нейроны и соответствующие им диаграммы Венна [65]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_09.gif)
![Сеть Мак-Каллока \delta=2 [65]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_12.gif)
![Логически устойчивая сеть Мак-Каллока \delta=2 [65]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_13.gif)
![Формальные нейроны с равноправными запрещающими и разрешающими входами [68]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_14sm.gif)
![Схемы RS-триггеров на пороговых и формальных нейронах [68]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_15.gif)
![Сеть Хопфилда в качестве структурно организованной ассоциативной памяти [70]](/EDI/14_06_16_2/1465856498-31733/tutorial/593/objects/4/files/04_16.gif)