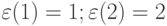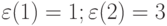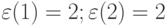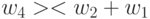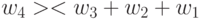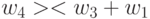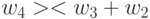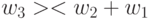| Россия, Москва, МЭИ, 2006 |
Нейрофизиологический и формально-логический базис нейроподобных вычислений
В разделе 4.6 показано, что комбинаторная схема порождения совместных инверсий отношения "больше-меньше" использует так называемую [85] е-спецификацию, элементы которой характеризуют количество компонент весового вектора, стоящих в левой (е(1)) и правой (е(2)) части инвертируемого отношения. В частности, для 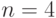
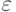 -спецификация имеет вид
-спецификация имеет вид ![[\varepsilon(1) = 1;\varepsilon(2) = 2]](/sites/default/files/tex_cache/a18b3eee234e350893bcd321dc3de76d.png) ;
; ![[\varepsilon(1) = 1;\varepsilon(2) = 3]](/sites/default/files/tex_cache/0e1a368f9989d2ad1dc6e3e55cea7aeb.png) ;
; ![[\varepsilon(1) = 2; \varepsilon(2) = 2]](/sites/default/files/tex_cache/d1bdb26312c307f213dacaaf81ecb042.png) . Такая спецификация систематизирует перечисление конечного множества инвертируемых отношений "больше-меньше" (неоднозначных неравенств, в случае
. Такая спецификация систематизирует перечисление конечного множества инвертируемых отношений "больше-меньше" (неоднозначных неравенств, в случае 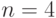 представленных в
табл. 4.11), которые еще необходимо доопределить множеством кратных инверсий значений свертки по правилу:
представленных в
табл. 4.11), которые еще необходимо доопределить множеством кратных инверсий значений свертки по правилу:
- По индексам левой (
 ) и правой (
) и правой (  ) части инвертируемых базовых отношений "больше-меньше" строятся векторы
) части инвертируемых базовых отношений "больше-меньше" строятся векторы 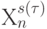 и
и 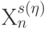 , у которых "единичные" значения отвечают индексам переменных, входящих в эти отношения.
, у которых "единичные" значения отвечают индексам переменных, входящих в эти отношения. - Слиянием по "ИЛИ" строится вектор
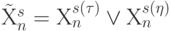
- В векторах
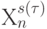 и
и 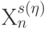 одновременно изменяются на "единичные" те компоненты
одновременно изменяются на "единичные" те компоненты 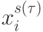 и
и 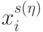 , у которых индекс
, у которых индекс  отвечает условию
отвечает условию  . В результате множество исходных инверсий отношения "больше-меньше" (после ассоциативного суммирования - транспозиций ), включая и кратные, для
. В результате множество исходных инверсий отношения "больше-меньше" (после ассоциативного суммирования - транспозиций ), включая и кратные, для  примет вид:
примет вид: -
 ;
; 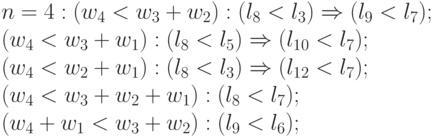
На основе этих транспозиций значений свертки строятся цепочки транзитивных транспозиций, которые отвечают классическим правилам преобразования неравенств: неравенство только усилится, если к
"большему" прибавить "большее" или из "меньшего" вычесть "большее". В нашем случае существует только три цепочки транзитивных транспозиций (без учета кратных):
-
 ;
; -
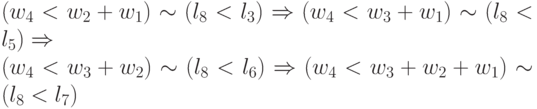 ;
; -
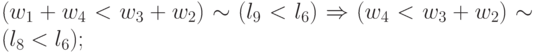 .
.
(Здесь символ 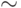 представляет отношение эквивалентности).
представляет отношение эквивалентности).
Отсюда: независимо можно осуществить только транспозиции, принадлежащие различным транзитивным цепочкам, общее количество которых в нашем случае не превышает 3 (без учета кратных), а сами транспозиции можно выполнить только между двумя смежными значениями индекса свертки  .
.
Выбрав определенную стратегию анализа цепочек транзитивных транспозиций, можно, не зная конкретных численных значений весовых коэффициентов, перечислить все подстановки значений свертки 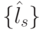 и отвечающие им подстановки индексов
и отвечающие им подстановки индексов  :
:
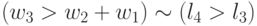 :
:
-
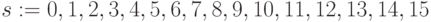 ;
; -
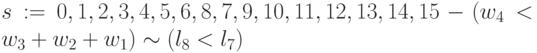 ;
; -
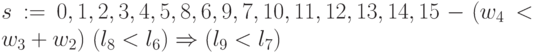 ;
; 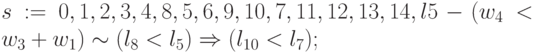
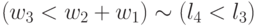 :
:
-
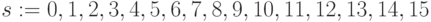 ;
; -
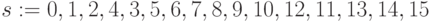 ;
; -
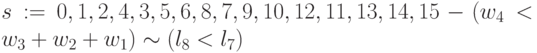 ;
; -
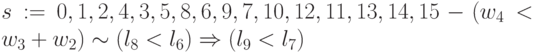 ;
; -
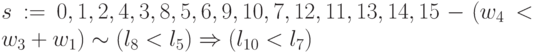 ;
; 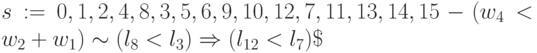
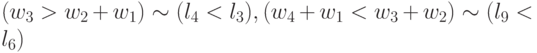 :
:
-
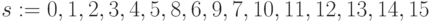 ;
; -
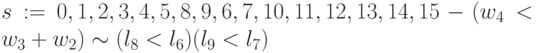 ;
; -
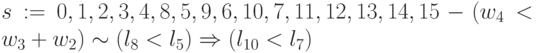 ;
;
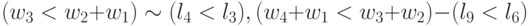 :
:
-
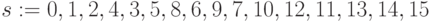 ;
; -
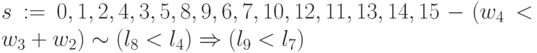 ;
; -
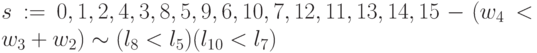 ;
; -
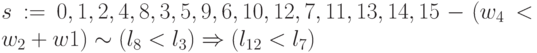 .
.
Здесь подстановки образуют пары: в первом подмножестве - 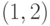 ,
, 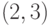 ,
, 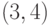 , во втором подмножестве -
, во втором подмножестве - 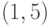 ,
, 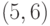 ,
, 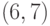 ,
, 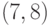 ,
, 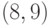 , в третьем подмножестве -
, в третьем подмножестве - 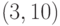 ,
, 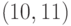 и в четвертом подмножестве -
и в четвертом подмножестве - 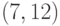 ,
, 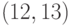 ,
, 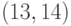 . Поэтому отношение частичного порядка для элементов
. Поэтому отношение частичного порядка для элементов 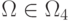 обеспечивается правилом перечисления подстановок из одного и того же подмножества, в котором каждая последующая подстановка отличается от предыдущей только одной транспозицией (с точностью до кратных транспозиций).
обеспечивается правилом перечисления подстановок из одного и того же подмножества, в котором каждая последующая подстановка отличается от предыдущей только одной транспозицией (с точностью до кратных транспозиций).
Чтобы перейти от элементов дистрибутивной структуры 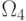 к порождающим ее значениям весовых коэффициентов
к порождающим ее значениям весовых коэффициентов  , достаточно одним из стандартных способов найти решения систем неравенств, отвечающих каждой приведенной выше подстановке индексов
, достаточно одним из стандартных способов найти решения систем неравенств, отвечающих каждой приведенной выше подстановке индексов  . В частности, простейшим методом "проб и ошибок" можно получить все целочисленные значения весовых коэффициентов (табл. 4.12 для
. В частности, простейшим методом "проб и ошибок" можно получить все целочисленные значения весовых коэффициентов (табл. 4.12 для 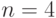 ). В первой графе
табл. 4.12 указан порядковый номер подстановки индексов
). В первой графе
табл. 4.12 указан порядковый номер подстановки индексов  , а первая строка соответствует лексикографическому порядку их перечисления. Из данных этой таблицы видно, что в случае
, а первая строка соответствует лексикографическому порядку их перечисления. Из данных этой таблицы видно, что в случае 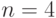 для решения задач оптимального синтеза (много)пороговых моделей требуется всего 14 образующих весовых векторов, у которых компоненты переименуются с помощью конечных групп подстановок и инверсий знака.
для решения задач оптимального синтеза (много)пороговых моделей требуется всего 14 образующих весовых векторов, у которых компоненты переименуются с помощью конечных групп подстановок и инверсий знака.
| № | 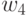 |
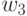 |
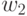 |
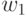 |
Условие |
|---|---|---|---|---|---|
| 1 | 8 | 4 | 2 | 1 | Lex |
| 2 | 10 | 6 | 3 | 2 | 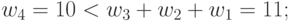 |
| 3 | 10 | 4 | 3 | 2 |  |
| 4 | 8 | 4 | 3 | 2 | 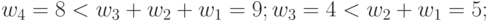 |
| 5 | 10 | 7 | 4 | 2 | 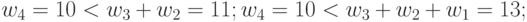 |
| 6 | 8 | 6 | 4 | 1 | 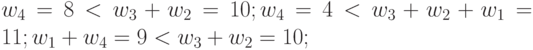 |
| 7 | 10 | 6 | 5 | 2 | 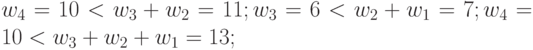 |
| 8 | 11 | 8 | 7 | 2 | 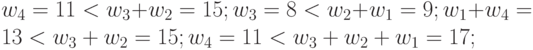 |
| 9 | 10 | 8 | 4 | 3 | 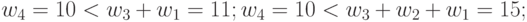 |
| 10 | 8 | 7 | 4 | 2 | 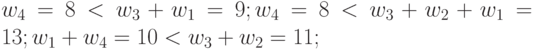 |
| 11 | 10 | 7 | 5 | 4 | 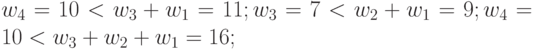 |
| 12 | 10 | 8 | 6 | 3 | 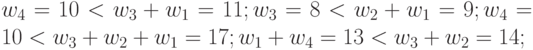 |
| 13 | 10 | 8 | 6 | 5 | 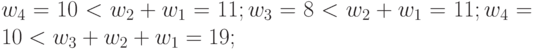 |
| 14 | 10 | 8 | 7 | 4 | 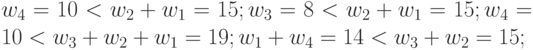 |
Если нейроподобный теоретико-групповой компилятор использовать при создании ЭВМ классической архитектуры, то для минимизации библиотеки стандартных элементов, реализуемых непосредственно в технологическом процессе, можно использовать только образующие булевы функции [101, 102].
Метод образующих булевых функций широко использовался в теории и практике многофункциональных логических модулей, к которым относятся и (много)пороговые элементы и их модели. В случае (много) пороговых моделей он позволяет существенным образом снизить вариации вектора порогов 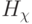 , ограничив их конечным множеством целочисленных значений. Для этого достаточно все множество булевых функций
, ограничив их конечным множеством целочисленных значений. Для этого достаточно все множество булевых функций 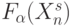 разбить на смежные (по группам дистрибутивной структуры
разбить на смежные (по группам дистрибутивной структуры  ) классы [103]:
) классы [103]: ![\{F_{\alpha}{X^{s}_{n})\} =\bigcup\{F_{\alpha}(\Psi [Х_n^s])\}](/sites/default/files/tex_cache/90a2b5a8a86180d291c1aab728f44154.png) , а вектор порогов
, а вектор порогов 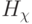 определить в целочисленном пространстве
определить в целочисленном пространстве 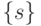 и только для образующих булевых функций
и только для образующих булевых функций 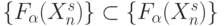 , где теоретико-множественное объединение (
, где теоретико-множественное объединение (  ) берется по образующим булевым функциям с индексами
) берется по образующим булевым функциям с индексами 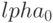 .
.
Схема поиска множества образующих для заданного класса булевых функций:
- Разбить весь класс булевых функций на подклассы с одинаковой первичной спецификацией [90]
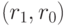 , которая отражает общее количество "единиц"
, которая отражает общее количество "единиц" 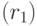 и "нулей"
и "нулей"  в таблице истинности булевых функций, принадлежащих данному подклассу:
в таблице истинности булевых функций, принадлежащих данному подклассу: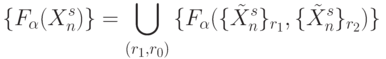
где:
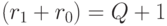 , a
, a 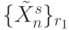 ,
, 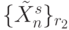 - подмножества входных векторов, на которых булева функция
- подмножества входных векторов, на которых булева функция 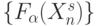 принимает соответственно "единичное" и "нулевое" значение. Количество подклассов с одинаковой первичной спецификацией можно ограничить условием
принимает соответственно "единичное" и "нулевое" значение. Количество подклассов с одинаковой первичной спецификацией можно ограничить условием  , нарушение которого приводит к подклассам инверсных булевых функций с инвертированными образующими.
, нарушение которого приводит к подклассам инверсных булевых функций с инвертированными образующими. - Разбить на смежные классы (по отношению к группам
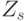 и
и 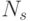 ) под-классы булевых функций с одинаковой первичной спецификацией:
) под-классы булевых функций с одинаковой первичной спецификацией:![\{F_{\alpha}(\{X^s_n\}_{r_1},\{X^s_n\}_{r_2})\} = \bigcup{ \{ F_{\alpha_0(Ф)}(Ф[X^s_n]) \} }](/sites/default/files/tex_cache/b236d049a72965755f0c16f563e2854a.png)
где
![Ф[X^s_n]](/sites/default/files/tex_cache/f20d14a5a57d96a44afb8bf3a7e4c8e2.png) представляет собой поочередно выполняемые преобразования
представляет собой поочередно выполняемые преобразования ![N_{s} [X^{s}_{n} ]](/sites/default/files/tex_cache/4d2058ecfb59c6000ca3b4ddc2bf893c.png) и
и ![Z_{s} [X^{s}_{n} ]](/sites/default/files/tex_cache/50a36de06594547d709f6466ae2da4e1.png) , а теоретико-множественные объединения берутся по образующим по классам смежности
, а теоретико-множественные объединения берутся по образующим по классам смежности 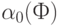 :
: 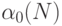 ,
, 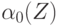 соответственно, в качестве которых может выступать любая функция из класса.
соответственно, в качестве которых может выступать любая функция из класса. - Объединить классы смежности по группе
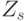 , если хотя бы одна из функций класса принадлежит одному и тому же классу смежности по группе
, если хотя бы одна из функций класса принадлежит одному и тому же классу смежности по группе 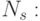
![\{F_{\alpha_0(D_s)}(D_s[X^s_n])\} = \bigcup{ \{ F_{\alpha_0(Z)}(Z_s[X^s_n]) \} }](/sites/default/files/tex_cache/3c284bcbc0f9dd60553112a290dca54b.png)
где
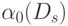 - индекс образующей из класса смежных по группе переименования переменных
- индекс образующей из класса смежных по группе переименования переменных 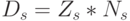 , а теоретико-множественное объединение берется по образующим для классов, смежных по группе
, а теоретико-множественное объединение берется по образующим для классов, смежных по группе 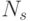 , с индексом
, с индексом 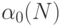 .
. - Объединить классы смежности по группам
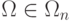 , если их образующие
, если их образующие 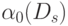 удовлетворяют условию минимально пороговой реализации с одинаковым рангом для всех компонент вектора порогов:
удовлетворяют условию минимально пороговой реализации с одинаковым рангом для всех компонент вектора порогов:![\{F_{\alpha_0(\Psi)}(\Psi[X^s_n])\} = \bigcup{ \{ F_{\alpha_0(\Omega)}(Z_s[X^s_n]) \} }](/sites/default/files/tex_cache/dd557ad875b97c1cdb8f191b536aba0e.png)
Здесь
 - индекс образующей для классов смежных булевых функций по группам дистрибутивной структуры
- индекс образующей для классов смежных булевых функций по группам дистрибутивной структуры  , а компоненты вектора порогов
, а компоненты вектора порогов 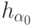 ,
, 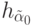 для образующих
для образующих  и
и  имеют одинаковый ранг, если
имеют одинаковый ранг, если  , где
, где 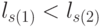 .
.
При  (табл. 4.13) требуется всего 13 образующих (без учета инверсных) для смежных по группам дистрибутивной структуры W классов, объединение которых и дает все множество булевых функций от трех переменных:
(табл. 4.13) требуется всего 13 образующих (без учета инверсных) для смежных по группам дистрибутивной структуры W классов, объединение которых и дает все множество булевых функций от трех переменных:
-
 ;
; -
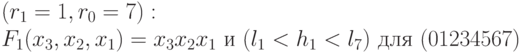 ;
; -
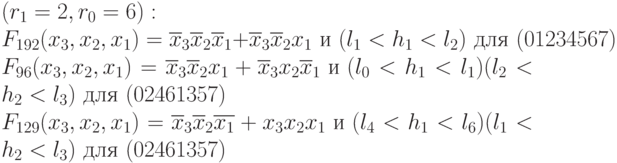 ;
; -
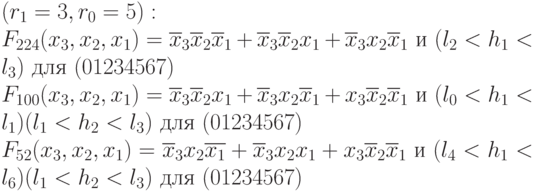 ;
; -
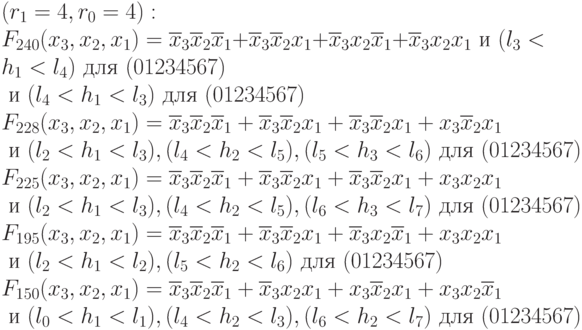 ;
;
| Первичная спецификация булевых функций | (0,8) | (1,7) | (2,6) | (3,5) | (4,4) |
|---|---|---|---|---|---|
| Количество образующих булевых функций | 1 | 1 | 3 | 3 | 5 |
| Мощность классов смежных булевых функций | 1 | 8 | 12 | 24 | 14 |
| 12 | 24 | 24 | |||
| 4 | 8 | 24 | |||
| 6 | |||||
| 2 | |||||
| Итого булевых функций: (1+8+28+56)*2+70=256 | 1 | 8 | 28 | 56 | 70 |