НОУ ИНТУИТ | Введение в Octave. Лекция 11: Обработка результатов эксперимента. Метод наименьших квадратов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

11.5 Подбор зависимостей методом наименьших квадратов в Octave

11.5.1 Функции Octave, используемые для подбора зависимости МНК

Для решения задач подбора аналитических зависимостей по экспериментальным данным можно использовать следующие функции Octave:

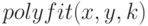— функция подбора коэффициентов полинома -й степени методом наименьших квадратов ( — массив абсцисс экспериментальных точек, — массив ординат экспериментальных точек, — степень полинома), функция возвращает массив коэффициентов полинома;
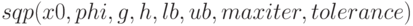— функция поиска минимума (функция подробно описана в десятой главе);
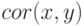— функция вычисления коэффициента корреляции ( — массив абсцисс экспериментальных точек, — массив ординат экспериментальных точек);
— функция вычисления среднего арифметического.

11.5.2 Примеры решения задач

Пример 11.1. В ->Основах химии-> Д.И. Менделеева приводятся данные о растворимости азотнокислого натрия 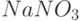NaNO_3 в зависимости от температуры воды. В 100 частях воды (табл. 11.3) растворяется следующее число условных частей 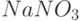NaNO_3 при соответствующих температурах. Требуется определить растворимость азотнокислого натрия при температуре 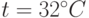t = 32°C в случае линейной зависимости и найти коэффициент корреляции.

Решение задачи 11.1 с комментариями приведено в листинге 11.1.

увеличить изображение
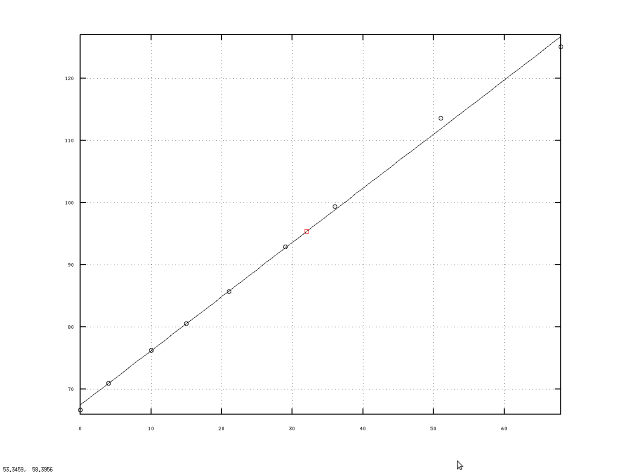
Рис. 11.2. Иллюстрация к примеру 11.1

	
% Ввод экспериментальных данных
X=[0 4 10 15 21 29 36 51 68];
Y=[66.7 71.0 76.3 80.6 85.7 92.9 99. 4 113.6 125.1];
% Вычисление вектора коэффициентов полинома y=a1*x+a2
[ a]= polyfit (X, Y, 1)
% Вычисление значения полинома y=a1*x+a2 в точке t=32
t =32; yt=a(1)*t+a(2)
% Построение графика полинома y=a1*x+a2, экспериментальных точек
% и значения в заданной точке в одной графической области
x =0:68; y=a(1)*x+a(2);
plot (X, Y, ’ok’, x, y, ’-k’, t, yt, ’*k’)
grid on;
% Вычисление коэффициента корреляции
k =cor(x, y)
% Результаты вычислений
a = 0.87064 67.50779
yt = 95.368
k = 1

Листинг 11.1. Решение к примеру 11.1

На рис. 11.2 приведено графическое решение этой задачи, изображены экспериментальные точки, линия регрессии 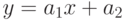y=a_1x+a_2 , на котором отмечена точка t = 32 .

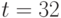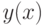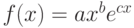Пример 11.2. В результате эксперимента получена табличная зависимость y(x) (см. табл. 11.4). Подобрать аналитическую зависимость $Y=ax^be^{cx}$ методом наименьших квадратов. Вычислить ожидаемое значение в точках 2, 3, 4. Вычислить индекс корреляции. Решение задачи подбора параметров функции $f(x)=ax^be^{cx}$ в Octave возможно двумя способами:

Таблица 11.4. Данные к примеру 11.2
x	1	1,4	1,8	2,2	2,6	3	3,4	3,8	4,2	4,6	5	5,4	5,8
y	0,7	0,75	0,67	0,62	0,51	0,45	0,4	0,32	0,28	0,25	0,22	0,16	0,1

Решение задачи путём поиска минимума функции (11.15)^{2Может не получится решать задачу подбора зависимости ->в лоб-> путём оптимизации функции 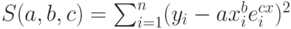, это связано с тем, что при решении задачи оптимизации с помощью sqp итерационными методами может возникнуть проблема возведения отрицательного числа в дробную степень [3, c.70–71]. Да и с точки зрения математики, если есть возможность решать линейную задачу вместо нелинейной, то лучше решать линейную.}. После чего надо пересчитать значение коэффициента a по формуле .
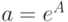Формирование системы линейных алгебраических уравнений (11.16)^{3Следует помнить, что при отрицательных значениях y необходимо будет решать проблему замены 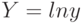.} и её решение.

Рассмотрим последовательно оба варианта решения задачи.

Способ 1.

Функция (11.15) реализована в Octave с помощью функции 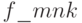$f\_mnk$ . Полный текст программы решения задачи способом 1 с комментариями приведён на листинге 11.2. Вместо коэффициентов 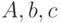A, b, c из формул (11.15)–(11.16) в программе на Octave используется массив .

	
function s=f_mnk( c )
% Переменные x,y являются глобальными, используются в нескольких функциях
	global x; global y;
	s =0;
	for i =1: length(x)
		s=s +(log(y(i))-c(1)-c(2)*log(x(i))*c(3)*x(i))^2;
	end
end
% _________________________________________________
global x; global y;
% Задание начального значения вектора c, при неправильном его
% определении, экстремум может быть найден неправильно.
c = [2; 1; 3];
% Определение координат экспериментальных точек
x=[1 1.4 1.8 2.2 2.6 3 3.4 3.8 4.2 4.6 5 5.4 5.8];
y=[0.7 0.75 0.67 0.62 0.51 0.45 0.4 0.32 0.28 0.25 0.22 0.16 0.1];
% Решение задачи оптимизации функции 11.15 с помощью sqp.
c=sqp(c,@f_mnk)
% Вычисление суммарной квадратичной ошибки для подобранной
% зависимости и вывод её на экран.
sum1=f_mnk( c )
% Формирование точек для построения графика подобранной кривой.
x1 = 1:0.1:6;
y1= exp(c(1)).*x1.^ c(2).*exp(c(3).*x1);
% Вычисление значений на подобранной кривой в заданных точках.
yr=exp(c(1)).*x.^ c(2).*exp(c(3).*x );
% Вычисление ожидаемого значения подобранной функции в точках x=[2,3,4]
x2 =[2 3 4 ]
y2= exp(c(1)).*x2.^c(2).*exp(c(3).*x2)
% Построение графика: подобранная кривая, f(x2) и экспериментальные точки.
plot(x1, y1, ’-r’, x, y, ’*b’, x2, y2, ’sk’);
% Вычисление индекса корреляции.
R=sqrt(1-sum((y-yr ).^ 2)/sum((y-mean(y)).^2))
% Результаты вычислений
c =
	0.33503
	0.90183
	-0.69337
sum1=0.090533
x2= 2 3 4
y2= 0.65272 0.47033 0.30475
R= 0.99533

Листинг 11.2. Решение к примеру 11.2 способ 1.

Таким образом подобрана зависимость 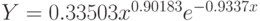$Y = 0.33503x^{0.90183}e^{-0.9337x}$ . Вычислено ожидаемое значение в точках 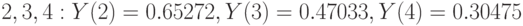2, 3, 4: Y (2) = 0.65272, Y (3) = 0.47033, Y (4) = 0.30475 . График подобранной зависимости вместе с экспериментальными точками и расчётными значениями изображён на рис. 11.3. Индекс корреляции равен 0.99533.

Способ 2.

Теперь рассмотрим решение задачи 11.2 путём решения системы 11.16. Решение с комментариями приведено в листинге 11.3. Результаты и графики при решении обоими способами полностью совпадают.

	
function s=f_mnk(c)
% Переменные x,y являются глобальными, используются в нескольких функциях
	global x;
	global y;
	s =0;
	for i =1: length(x)
		s=s+(log(y(i))-c(1)-c(2)*log(x(i))-c(3)*x(i))^2;
	end
end
%___________________________________
global x;
global y;
% Определение координат экспериментальных точек
x=[1 1.4 1.8 2.2 2.6 3 3.4 3.8 4.2 4.6 5 5.4 5.8];
y=[0.7 0.75 0.67 0.62 0.51 0.45 0.4 0.32 0.28 0.25 0.22 0.16 0.1];
% Формирование СЛАУ (11.16)
G=[length(x) sum(log(x)) sum(x); sum(log(x)) sum(log(x).*log(x
	))sum(x.*log(x)); sum(x) sum(x.*log(x)) sum(x.*x)];
H=[sum(log(y)); sum(log(y).*log(x)); sum(log(y).*x)];
% Решение СЛАУ методом Гаусса с помощью функции rref.
C=rref([G H]); n=size(C); c=C(:, n(2))
% Вычисление суммарной квадратичной ошибки для подобранной
% зависимости и вывод её на экран.
sum1=f_mnk(c)
% Формирование точек для построения графика подобранной кривой.
x1 = 1:0.1:6;
y1= exp(c(1)).*x1.^c(2).*exp(c(3).*x1);
% Вычисление значений на подобранной кривой в заданных точках.
yr=exp(c(1)).*x.^c(2).*exp(c(3).*x);
% Вычисление ожидаемого значения подобранной функции в точках x=[2,3,4]
x2 =[2 3 4 ]
y2= exp(c(1)).*x2.^c(2).*exp(c(3).*x2)
% Построение графика: подобранная кривая, f(x2) и экспериментальные точки.
plot(x1, y1, ’-r’, x, y, ’*b’, x2, y2, ’sk’);
% Вычисление индекса корреляции.
R=sqrt(1-sum((y-yr).^2)/sum((y-mean(y)).^2))

Листинг 11.3. Решение к примеру 11.2 способ 2.

Дальше >>

Авторизоваться

Введение в Octave

Обработка результатов эксперимента. Метод наименьших квадратов

11.5 Подбор зависимостей методом наименьших квадратов в Octave

11.5.1 Функции Octave, используемые для подбора зависимости МНК

11.5.2 Примеры решения задач

Вопросы и ответы