|
Возможна ли разработка приложения на Octave с GUI? |
Обработка результатов эксперимента. Метод наименьших квадратов
11.2.1 Подбор коэффициентов линейной зависимости
Для подбора параметров линейной функции 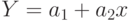 , составим функцию (11.1) для линейной зависимости:
, составим функцию (11.1) для линейной зависимости:
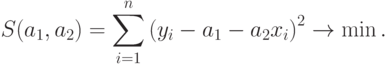 |
( 11.4) |
Продифференцировав функцию  по
по 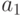 и
и 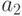 , получим систему уравнений:
, получим систему уравнений:
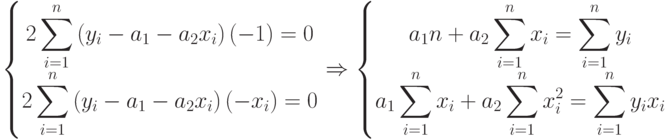 |
( 11.5) |
решив которую, определим коэффициенты функции 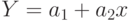 :
:
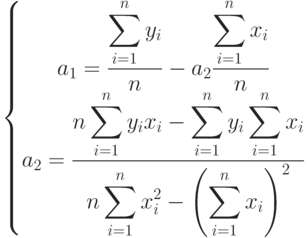
11.2.2 Подбор коэффициентов полинома k–й степени
Для определения параметров зависимости 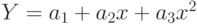 составим функцию
составим функцию 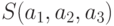 (11.1):
(11.1):
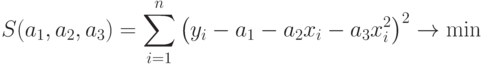 |
( 11.7) |
После дифференцирования S по 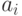 ,
,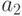 и
и  получим систему линейных алгебраических уравнений:
получим систему линейных алгебраических уравнений:
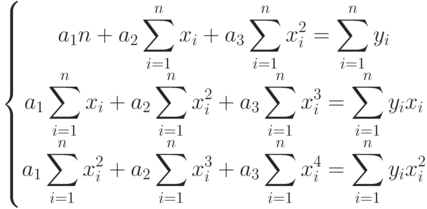 |
( 11.8) |
Решив систему (11.8), найдём значения параметров a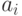 ,
,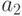 и
и  .
.
Аналогично определим параметры многочлена третьей степени: . Составим функцию
. Составим функцию  :
:
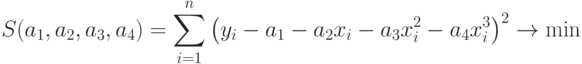 |
( 11.9) |
После дифференцирования  по
по 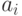 ,
,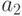 ,
, и
и 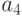 , система линейных алгебраических уравнений для вычисления параметров a
, система линейных алгебраических уравнений для вычисления параметров a 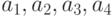 примет вид:
примет вид:
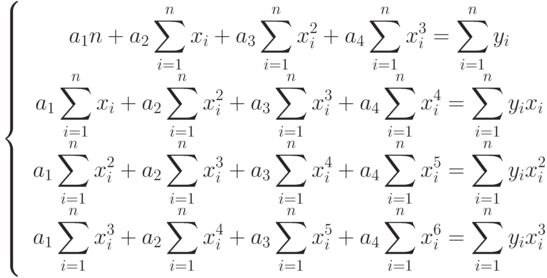 |
( 11.10) |
Решив систему (11.10), найдём коэффициенты 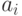 ,
,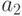 ,
, и
и 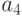 .
.
В общем случае система уравнений для вычисления параметров 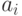 многочлена k-й степени
многочлена k-й степени  имеет вид:
имеет вид:
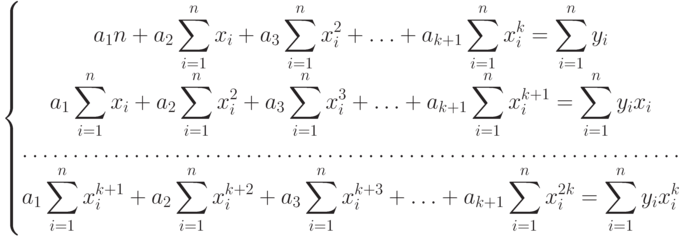 |
( 11.11) |
В матричном виде систему (11.11) можно записать
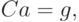 |
( 11.12) |
Элементы матрицы C и вектора g рассчитываются по формулам
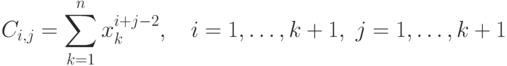 |
( 11.13) |
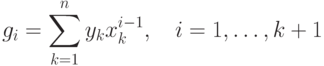 |
( 11.14) |
Решив систему (11.12), определим параметры зависимости  .
.
