Обработка результатов эксперимента. Метод наименьших квадратов

11.3 Уравнение регрессии и коэффициент корреляции

Линия, описываемая уравнением вида 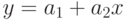, называется линией регрессии на , параметры 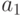и 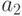называются коэффициентами регрессии и определяются формулами (11.6).

Чем меньше величина 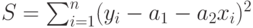, тем более обоснованно предположение, что экспериментальные данные описываются линейной функцией. Существует показатель, характеризующий тесноту линейной связи между и , который называется коэффициентом корреляции и рассчитывается по формуле:

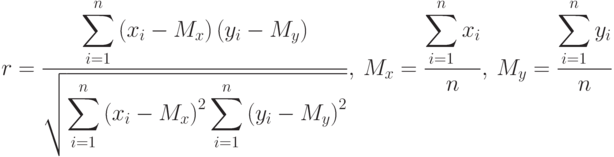( 11.18)

Значение коэффициента корреляции удовлетворяет соотношению .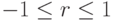

Чем меньше отличается абсолютная величина от единицы, тем ближе к линии регрессии располагаются экспериментальные точки. Если , то все экспериментальные точки находятся на линии регрессии. Если коэффициент корреляции близок к нулю, то это означает, что между и не существует линейной связи, но между ними может существовать зависимость, отличная от линейной.

Для того, чтобы проверить, значимо ли отличается от нуля коэффициент корреляции, можно использовать критерий Стьюдента. Вычисленное значение критерия определяется по формуле:

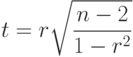( 11.19)

Рассчитанное по формуле (11.19) значение сравнивается со значением, взятым из таблицы распределения Стьюдента (см. табл. 11.2) в соответствии с уровнем значимости (стандартное значение 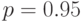) и числом степеней свободы 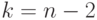. Если полученная по формуле (11.19) величина больше табличного значения, то коэффициент корреляции значимо отличен от нуля.

Таблица 11.2. Таблица распределения Стьюдента

k\p	0,99	0,98	0,95	0,90	0,80	0,70	0,60
1	63,657	31,821	12,706	6,314	3,078	1,963	1,376
2	9,925	6,965	4,303	2,920	1,886	1,386	1,061
3	5,841	4,541	3,182	2,353	1,638	1,250	0,978
4	4,604	3,747	2,776	2,132	1,533	1,190	0,941
5	4,032	3,365	2,571	2,05	1,476	1,156	0,920
6	3,707	3,141	2,447	1,943	1,440	1,134	0,906
7	3,499	2,998	2,365	1,895	1,415	1,119	0,896
8	3,355	2,896	2,896	1,860	1,387	1,108	0,889
9	3,250	2,821	2,261	1,833	1,383	1,100	0,883
10	3,169	2,764	2,228	1,812	1,372	1,093	0,879
11	3,106	2,718	2,201	1,796	1,363	1,088	0,876
12	3,055	2,681	2,179	1,782	1,356	1,083	0,873
13	3,012	2,681	2,179	1,782	1,356	1,083	0,873
14	2,977	2,624	2,145	1,761	1,345	1,076	0,868
15	2,947	2,602	2,131	1,753	1,341	1,074	0,866
16	2,921	2,583	2,120	1,746	1,337	1,071	0,865
17	2,898	2,567	2,110	1,740	1,333	1,069	0,863
18	2,878	2,552	2,101	1,734	1,330	1,067	0,862
19	2,861	2,539	2,093	1,729	1,328	1,066	0,861
20	2,845	2,528	2,086	1,725	1,325	1,064	0,860
21	2,831	2,518	2,080	1,721	1,323	1,063	0,859
22	2,819	2,508	2,074	1,717	1,321	1,061	0,858
23	2,807	2,500	2,069	1,714	1,319	1,060	0,858
24	2,797	2,492	2,064	1,711	1,318	1,059	0,857
25	2,779	2,485	2,060	1,708	1,316	1,058	0,856
26	2,771	2,479	2,056	1,706	1,315	1,058	0,856
27	2,763	2,473	2,052	1,703	1,314	1,057	0,855
28	2,756	2,467	2,048	1,701	1,313	1,056	0,855
29	2,750	2,462	2,045	1,699	1,311	1,055	0,854
30	2,704	2,457	2,042	1,697	1,310	1,055	0,854
40	2,660	2,423	2,021	1,684	1,303	1,050	0,851
60	2,612	2,390	2,000	1,671	1,296	1,046	0,848
120	2,617	2,358	1,980	1,980	1,289	1,041	0,845
	2,576	2,326	1,960	1,645	1,282	1,036	0,842