|
Возможна ли разработка приложения на Octave с GUI? |
Задачи линейной алгебры
5.5 Решение некоторых задач алгебры матриц
Напомним основные определения алгебры матриц. Если m _ n выражений расставлены в прямоугольной таблице из  строк и
строк и  столбцов, то говорят о матрице размера
столбцов, то говорят о матрице размера  :
:
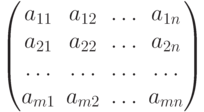 |
( 5.1) |
Выражения a ij называют элементами матрицы. Элементы 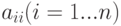 , стоящие в таблице на линии, проходящей из левого верхнего угла в правый нижний угол квадрата
, стоящие в таблице на линии, проходящей из левого верхнего угла в правый нижний угол квадрата  , образуют главную диагональ матрицы.
, образуют главную диагональ матрицы.
 |
( 5.2) |
Матрица размером  называется прямоугольной (5.1). В случае если
называется прямоугольной (5.1). В случае если  , матрицу называют квадратной матрицей порядка n.
, матрицу называют квадратной матрицей порядка n.
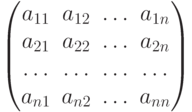 |
( 5.3) |
В частности, матрица типа  — это вектор–строка:
— это вектор–строка: 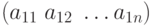 .
.
Матрица размером 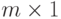 является вектором–столбцом:
является вектором–столбцом: 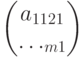 am1
am1
Число (скаляр) можно рассматривать как матрицу типа 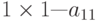 . Квадратная матрица
. Квадратная матрица 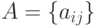 размером
размером  называется:
называется:
- нулевой, если все её элементы равны нулю:
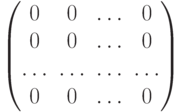 _
_ - верхней треугольной, если все элементы, расположенные ниже главной диагонали, равны нулю:
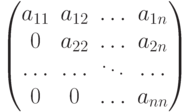 _
_ - нижней треугольной, если все элементы, расположенные выше главной диагонали, равны нулю:
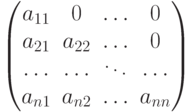 _
_ - диагональной, если все элементы, кроме элементов главной диагонали, равны нулю:
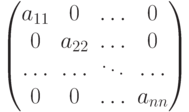 _
_ - единичной, если элементы главной диагонали равны единице, а все остальные нулю:
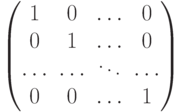
Определителем (детерминантом) матрицы  является число
является число  или Δ, вычисляемое по правилу:
или Δ, вычисляемое по правилу: 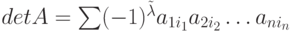 , где сумма распределена на всевозможные перестановки
, где сумма распределена на всевозможные перестановки 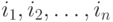 элементов
элементов 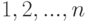 и, следовательно, содержит
и, следовательно, содержит 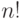 слагаемых, причём
слагаемых, причём  , если перестановка чётная, и
, если перестановка чётная, и  , если перестановка нечётная.
, если перестановка нечётная.
Квадратная матрица  называется невырожденной, если её определитель отличен от нуля
называется невырожденной, если её определитель отличен от нуля 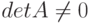 . В противном случае
. В противном случае 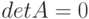 матрица называется вырожденной или сингулярной.
матрица называется вырожденной или сингулярной.
С матрицами можно проводить операции сравнения, сложения и умножения.
Две матрицы 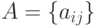 и
и 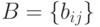 считаются равными, если
они одного типа, то есть имеют одинаковое число строк и столбцов, и соответствующие элементы их равны
считаются равными, если
они одного типа, то есть имеют одинаковое число строк и столбцов, и соответствующие элементы их равны  .
.
Суммой двух матриц 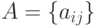 и
и 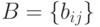 одинакового типа называется матрица
одинакового типа называется матрица 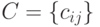 того же типа, элементы которой равны сумме соответствующих элементов матриц
того же типа, элементы которой равны сумме соответствующих элементов матриц 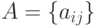 и
и 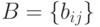 :
: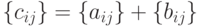 .
.
Разность матриц 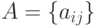 и
и 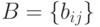 определяется аналогично:
определяется аналогично: 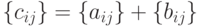 .
.
Произведением числа 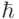 и матрицы
и матрицы 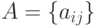 (или умножением матрицы на число) называется матрица, элементы которой получены умножением всех элементов матрицы
(или умножением матрицы на число) называется матрица, элементы которой получены умножением всех элементов матрицы 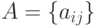
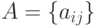 на число
на число  .
.
Произведением матриц 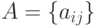 размерностью
размерностью  и
и 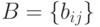 размерностью
размерностью  является матрица
является матрица 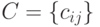 размерностью
размерностью  , каждый элемент которой можно представить формулой
, каждый элемент которой можно представить формулой 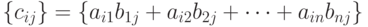 , где
, где 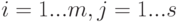 .
.
Таким образом, произведение матриц 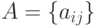 и
и 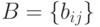 имеет смысл тогда и только тогда, когда количество строк матрицы
имеет смысл тогда и только тогда, когда количество строк матрицы 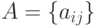 совпадает с количеством столбцов матрицы
совпадает с количеством столбцов матрицы 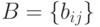 . Кроме того, произведение двух матриц не обладает переместительным законом, то есть
. Кроме того, произведение двух матриц не обладает переместительным законом, то есть 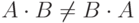 . В тех случаях, когда
. В тех случаях, когда  , матрицы
, матрицы 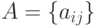 и
и 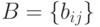 называются перестановочными.
называются перестановочными.
Если в матрице 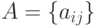 размерностью
размерностью  заменить строки соответствующими столбцами, то получится транспонированная матрица:
заменить строки соответствующими столбцами, то получится транспонированная матрица: 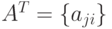 .
.
В частности, для вектора–строки 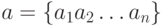 транспонированной матрицей является вектор–столбец:
транспонированной матрицей является вектор–столбец:
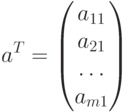
Обратной матрицей по отношению к данной матрице 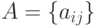 размерностью
размерностью  , называется матрица
, называется матрица  того же типа, которая, будучи умноженной как справа, так и слева на данную матрицу, в результате даёт единичную матрицу
того же типа, которая, будучи умноженной как справа, так и слева на данную матрицу, в результате даёт единичную матрицу 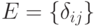 , где
, где 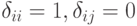 , при
, при 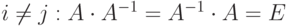 .
.
Нахождение обратной матрицы для данной называется обращением данной матрицы. Всякая неособенная матрица имеет обратную матрицу.
Перейдём к конкретным примерам.
Пример 5.2. Для матриц  и
и 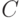 проверить выполнение следующих тождеств:
проверить выполнение следующих тождеств:
 |
( 5.4) |
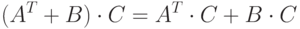 |
( 5.5) |
Из листинга 5.4 видно, что матрицы, получившиеся в результате вычисления левой и правой частей тождества (5.4), равны, следовательно, первое тождество истинно. Для исследования тождества (5.5) из левой части равенства вычитаем правую и получаем нулевую матрицу, что так же приводит к выводу об истинности тождества.
>>> A=[1 -2 0; -3 0 4 ]; B=[3 1; 2 0; -1 1 ]; C=[1 2; -1 0 ]; >>> (A*B) *C % Исследование тождества (5.4) ans = -2 -2 -14 -26 >>> A* (B*C) ans = -2 -2 -14 -26 >>> (A’+B) *C-(A’ * C+B*C) % Исследование тождества (5.5) ans = 0 0 0 0 0 0Листинг 5.4. Проверка матричных тождеств (пример 5.2).
Пример 5.3. Проверить является ли матрица симметрической. Квадратная матрица называется симметрической, если 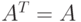 .
.
В листинге 5.5 видно, что в результате вычитания из матрицы  транспонированной матрицы
транспонированной матрицы 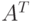 получена нулевая матрица, то есть тождество выполнено, и заданная матрица — симметрическая.
получена нулевая матрица, то есть тождество выполнено, и заданная матрица — симметрическая.
>>> A=[1 -0.5 1.5; - 0.50 2.5; 1.5 2.5 -2]; A - A’ ans = 0 0 0 0 0 0 0 0 0Листинг 5.5. Проверка симметрической матрицы (пример 5.3).
Пример 5.4. Проверить, является ли матрица кососимметрической. Квадратная матрица называется кососимметрической, если 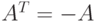 .
Проверив равенство для заданной матрицы (листинг 5.6), убеждаемся в его истинности.
.
Проверив равенство для заданной матрицы (листинг 5.6), убеждаемся в его истинности.
>>> A=[0 -0.25 0.75; 0.25 0 -1.25; -0.75 1.25 0]; A’+A ans = 0 0 0 0 0 0 0 0 0Листинг 5.6. Проверка кососимметрической матрицы (пример 5.4).
Пример 5.5. Проверить, является ли матрица ортогональной. Квадратная матрица называется ортогональной, если 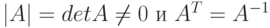 и
и  .
.
Для решения поставленной задачи необходимо вычислить определитель заданной матрицы и убедиться в том, что он не равен нулю. Затем следует транспонировать исходную матрицу и найти матрицу, обратную к ней. Если визуально сложно убедиться в том, что транспонированная матрица равна обратной, можно вычислить их разность. В результате должна получиться нулевая матрица (листинг 5.7).
>>> A= [ 0.5 0.7071 0.5; 0.7071 0 -0.7071; 0.5 -0.7071 0.5 ] A = 0.50000 0.70710 0.50000 0.70710 0.00000 -0.70710 0.50000 -0.70710 0.50000 >>> det (A) % Определитель матрицы A отличен от нуля ans = -0.99998 >>> A’-inv (A) % При вычитании из транспонированной матрицы A обратной % к ней матрицы получаем нулевую матрицу, значит A — ортогональная. ans = 0.0000e+00 -1.3562e-05 0.0000e+00 -1.3562e-05 0.0000e+00 1.3562e-05 0.0000e+00 1.3562e-05 0.0000e+00Листинг 5.7. Проверка ортогональности матрицы (пример 5.5).
Пример 5.6. Задана матрица  . Показать, что матрица
. Показать, что матрица 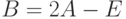 , где
, где 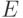 — единичная матрица — инволютивна. Квадратная матрица называется инволютивной, если
— единичная матрица — инволютивна. Квадратная матрица называется инволютивной, если  , где
, где 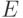 — единичная матрица.
— единичная матрица.
Решение задачи:
>>> A=[6 -15;2 -5]; B=2*A -eye ( 2 ); B^2 ans = 1 0 0 1
Пример 5.7. Решить матричные уравнения 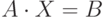 и
и 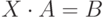 , выполнить проверку.
, выполнить проверку.
Матричное уравнение это уравнение вида 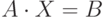 или
или 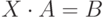 , где
, где  это неизвестная матрица. Если умножить матричное уравнение на матрицу обратную к
это неизвестная матрица. Если умножить матричное уравнение на матрицу обратную к  , то оно примет вид:
, то оно примет вид: 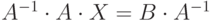 или
или 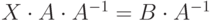 . Так как
. Так как 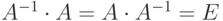 , а
, а 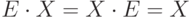 , то неизвестную матрицу
, то неизвестную матрицу  можно вычислить так:
можно вычислить так: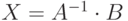 или
или 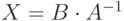 . Понятно, что матричное уравнение имеет единственное решение, если
. Понятно, что матричное уравнение имеет единственное решение, если  и
и  — квадратные матрицы
— квадратные матрицы  -го порядка, и определитель матрицы
-го порядка, и определитель матрицы  не равен нулю. Как решить матричное уравнение в Octave, показано в листинге 5.8.
не равен нулю. Как решить матричное уравнение в Octave, показано в листинге 5.8.
>>> A=[ 2 3; -2 6 ]; B=[2 5; 2 / 3 5 / 3 ]; % Решение уравнения A · X = B >>> X=A\B % Первый способ X = 0.55556 1.38889 0.29630 0.74074 >>> X=inv (A) *B % Второй способ X = 0.55556 1.38889 0.29630 0.74074 >>> A*X - B % Проверка A · X - B = 0 ans = 0.0000e+00 0.0000e+00 -3.3307e-16 -6.6613e-16 % Решение уравнения X · A = B >>> X=B/A % Первый способ X = 1.222222 0.222222 0.407407 0.074074 >>> X=B* inv (A) % Второй способ X = 1.222222 0.222222 0.407407 0.074074 >>> X*A - B % Проверка X · A _ B = 0 ans = 0.0000e+00 0.0000e+00 1.1102e-16 0.0000e+00Листинг 5.8. Решение матричного уравнения (пример 5.7).
