НОУ ИНТУИТ | Введение в Octave. Лекция 5: Задачи линейной алгебры

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

5.4.3 Функции, реализующие численные алгоритмы решения задач линейной алгебры

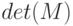det(M) — вычисляет определитель квадратной матрицы .

	
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ]; det (M)
ans = 682
>>> A=[1 0 -3;0 1 2; 2 0 -1]; det (A)
ans = 5

trace(M) — вычисляет след матрицы , то есть сумму элементов главной диагонали.

	
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ]
M =
	-1 1 -2 3
	4 5 -1 2
	3 -1 4 1
	-2 5 4 3
>>> trace(M)
ans = 11
>>> sum( diag (M) )
ans = 11

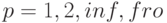norm(M[, p]) — возвращает различные виды норм матрицы в зависимости от , если аргумент p = 1, 2, inf, fro не задан, то вычисляется вторая норма матрицы .

	
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ];
>>> norm(M)% Вторая норма
ans = 8.5506
>>> norm(M, 2 )
ans = 8.5506
>>> norm(M, 1 ) % Первая норма
ans = 12
>>> norm(M, inf ) % Бесконечная норма
ans = 14
>>> norm(M, ’fro’ ) % Евклидова норма
ans = 11.916

cond(M[, p]) — возвращает число обусловленности матрицы , основанное на норме .

	
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ];
>>> cond(M)
ans = 3.3324
>>> cond(M, 2 )
ans = 3.3324
>>> cond(M, 1 )
ans = 6.4927
>>> cond(M, inf )
ans = 6.7742
>>> cond (M, ’fro’ )
ans = 5.7154

rcond(M) — вычисляет величину, обратную значению числа обусловленности матрицы относительно первой нормы, если полученная величина близка к единице, то матрица хорошо обусловлена, если к приближается к нулю, то плохо.

	
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ]; rcond (M)
ans = 0.1738

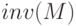inv(M) — возвращает матрицу обратную к .

	
>>> A=[1 0 -3;0 1 2; 2 0 -1]; invA=inv (A)
invA =
	-0.2  0  0.6
	 0.8  1 -0.4
	-0.4  0  0.2
>>> A_ invA % Проверка
ans =
	1 0 -5.5511e-17
	0 1  0
	0 0  1

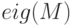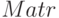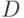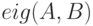eig(M) — возвращает вектор собственных значений матрицы , вызов функции в формате [Matr, D] = eig(M) даст матрицу Matr , столбцы которой — собственные векторы матрицы и диагональную матрицу , содержащую собственные значения матрицы , функция eig(A, B) , где и квадратные матрицы, выдаёт вектор обобщённых собственных значений.

	
>>> M=[3 -2;-4 1 ]
M =
	 3 -2
	-4 1
>>> eig (M)
ans =
	 5
	-1
>>> [ Matr,D]= eig (M)
Matr =
	 0.70711 0.44721
	-0.70711 0.89443
D =
Diagonal Matrix
	5  0
	0 -1
% Проверка A * M = M * D
>>> M * Matr
ans =
	 3.5355 -0.44721
	-3.5355 -0.89443
>>> Matr *D
ans =
	 3.5355 -0.44721
	-3.5355 -0.89443

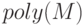poly(M) — возвращает вектор–строку коэффициентов характеристического полинома матрицы .

	
>>> M=[3 -2;-4 1 ]
M =
	3 -2
	-4 1
>>> poly(M)
ans = 1 -4 -5

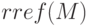rref (M) — осуществляет приведение матрицы к треугольной форме, используя метод исключения Гаусса.

	
>>> M=[3 -2 1 5; 6 -4 2 7; 9 -6 3 1 2 ]
M =
	3 -2 1 5
	6 -4 2 7
	9 -6 3 12
>>> rref (M)
ans =
	1  -0.66667     0.33333   0
	0 	0 			0 		  1
	0 	0 			0         0

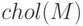chol(M) — возвращает разложение по Холецкому для положительно определённой симметрической матрицы .

	
>>> M=[10 1 1; 2 10 1; 2 2 10 ]
M =
	10 1 1
	2 10 1
	2 2 10
>>> chol(M)
ans =
	3.1623  0.31623  0.31623
	0       3.1464   0.28604
	0       0        3.1334
% Матрица не симметрическая
>>> A=[1 2; 1 1 ]; chol(A)
error: chol: matrix not positivedefinite
% Матрица содержит элементы < 0
>>> M=[3 -2 1 5; 6 -4 2 7; 9 -6 3 12 ];
>>> chol(M)
error: CHOL requires square matrix

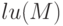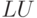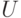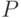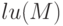lu(M) — выполняет –разложение, функция [L, U, P ] = lu(M) возвращает три матрицы: — нижняя треугольная, — верхняя треугольная и — матрица перестановок, причём $P\cdot A = L \cdot U$ . Функция lu(M) без параметров возвращает одну матрицу, которая в свою очередь, является комбинацией матриц и .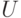

	
>>> M=[3 -2 1; 5 6 -4; 2 7 9 ];
>>> lu (M)
ans =
	5     6         -4
	0.6  -5.6       3.4
	0.4  -0.82143   13.393
>>> [ L, U, P]= lu (M)
L =
	1 		0 		  0
	0.6 	1         0
	0.4     -0.82143  1
U =
	5       6          -4
	0      -5.6        3.4
	0       0          13.393
P =
Permutation Matrix
	0 1 0
	1 0 0
	0 0 1
>>> L*U
ans =
	5  6 -4
	3 -2  1
	2  7  9
>>> P* M
ans =
	5  6 -4
	3 -2  1
	2  7  9
>>> lu(M)
ans =
	5      6        -4
	0.6   -5.6      3.4
	0.4   -0.82143  13.393
>>> triu( lu (M) )
ans =
	5      6             -4
	0     -5.6           3.4
	0      0             13.393
>>> tril( lu (M) )
ans =
	5       0           0
	0.6    -5.6         0
	0.4    -0.82143 13.393

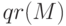qr(M) — выполняет 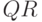–разложение, команда [Q, R, P ] = qr(M) возвращает три матрицы: ортогональную матрицу 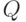, верхнюю треугольную матрицу 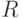и матрицу перестановок 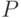, причём $A \cdot P = Q \cdot P$ .

	
>>> M=[3 -2 1; 5 6 -4;2 7 9 ];
>>> [Q, R, P]= qr (M)
Q =
	0.10102 -0.27448 0.95627
	-0.40406 0.86703 0.29155
	0.90914 0.41584 0.023324
R =
	9.8995   3.7376   0.10102
	0        8.662    4.3434
	0        0        4.3732
P =
Permutation Matrix
	0 0 1
	0 1 0
	1 0 0
>>> M *P - Q*R
ans =
-1.1102e-15   4.4409e-16	-4.4409e-16
-4.4409e-16   -1.7764e-15   0
0             0             -4.4409e-16

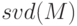svd(M) — возвращает вектор сингулярных чисел матрицы, при использовании в формате [U, S, V ] = svd(M) выполняет сингулярное разложение матрицы , выдаёт три матрицы: 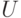— сформирована из ортонормированных собственных векторов, отвечающих наибольшим собственным значениям матрицы 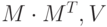$M \cdot M^T, V$ — состоит из ортонормированных собственных векторов матрицы 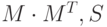$M \cdot M^T, S$ — диагональная матрица из сингулярных чисел (неотрицательных значений квадратных корней из собственных значений матрицы 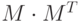$M \cdot M^T$ ), матрицы удовлетворяют условию $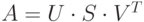A = U \cdot S \cdot V^T$ .

	
>>> M=[3 -2 1; 5 6 -4; 2 7 9 ];
>>> svd(M)
ans =
	11.7553
	8.5347
	3.7377
>>> [ U, S,V]=svd(M)
U =
	0.0057541  0.0207345  0.9997685
	0.2528901  -0.9673161  0.0186059
	0.9674779 0.2527245   -0.0108095
S =
Diagonal Matrix
	11.7553     0         0
	0           8.5347    0
	0           0         3.7377
V =
	0.27363  -0.50018   0.82155
	0.70421  -0.47761   -0.52534
	0.65515  0.72229    0.22154

Рассмотрим некоторые задачи линейной алгебры, которые могут быть решены с помощью описанных выше функций.

Дальше >>

Авторизоваться

Введение в Octave

Задачи линейной алгебры

5.4.3 Функции, реализующие численные алгоритмы решения задач линейной алгебры

Вопросы и ответы