|
Возможна ли разработка приложения на Octave с GUI? |
Задачи линейной алгебры
5.4 Функции для работы с матрицами и векторами
В Octave существуют специальные функции, предназначенные для работы с матрицами и векторами. Эти функции можно разделить на следующие группы:
- функции для работы с векторами;
- функции для работы c матрицами;
- функции, реализующие численные алгоритмы решения задач линейной алгебры.
Рассмотрим наиболее часто используемые функции.
5.4.1 Функции для работы с векторами
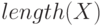 — определяет дину вектора
— определяет дину вектора  .
.
>>> X=[1 2 3 4 5 6 7 8 9 ]; >>> n=length (X) n = 9 >>> Y= [ - 2; - 1; 0; 1; 2 ] Y = -2 -1 0 1 2 >>> m=length (Y) m = 5
 — вычисляет произведение элементов вектора
— вычисляет произведение элементов вектора  .
.
>>> X=[1 2 3 4 5 6 7 8 9 ]; prod (X) ans = 362880
 — формирует вектор кумулятивного произведения — вектор того же типа и размера, что и X вида:
— формирует вектор кумулятивного произведения — вектор того же типа и размера, что и X вида: 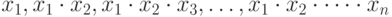 , каждый элемент которого рассчитывается по формулам
, каждый элемент которого рассчитывается по формулам 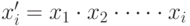 , то есть
, то есть  –й элемент вектора
–й элемент вектора  умножается на произведение всех предыдущих элементов.
умножается на произведение всех предыдущих элементов.
>>> X=[1 2 3 4 5 ]; cumprod (X) ans = 1 2 6 24 120
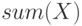 — вычисляет сумму элементов вектора
— вычисляет сумму элементов вектора  .
.
>>> X=[1 2 3 4 5 6 7 8 9 ]; sum(X) ans = 45
 — формирует вектор кумулятивной суммы — вектор того же типа и размера, что и
— формирует вектор кумулятивной суммы — вектор того же типа и размера, что и  вида
вида 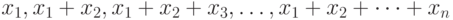 , каждый элемент которого рассчитывается по формуле:
, каждый элемент которого рассчитывается по формуле: 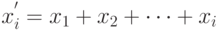 , то есть к
, то есть к  –му элементу вектора
–му элементу вектора  прибавляется сумма всех предыдущих элементов.
прибавляется сумма всех предыдущих элементов.
>>> X=[1 2 3 4 5 ]; cumsum(X) ans = 1 3 6 10 15
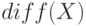 — формирует вектор вида
— формирует вектор вида 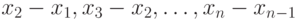 , размер которого на единицу меньше чем у вектора
, размер которого на единицу меньше чем у вектора  , а каждый элемент представляет собой разность между двумя соседними элементами массива
, а каждый элемент представляет собой разность между двумя соседними элементами массива  , то есть
, то есть 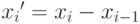 .
.
>>> X=[1 2 3 4 5 6 7 8 9 ]; diff(X) ans = 1 1 1 1 1 1 1 1
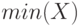 — находит минимальный элемент вектора
— находит минимальный элемент вектора  , вызов в формате
, вызов в формате ![[nomX, nom] = min(X)](/sites/default/files/tex_cache/3d77798c6e432e6f9d126c2cb1f15fdf.png) даёт возможность определить минимальный элемент
даёт возможность определить минимальный элемент  и его номер nom в массиве
и его номер nom в массиве  .
.
>>> X=[-1 2 3 9 -8 7 5 ]; >>> min(X) ans = -8 >>> [ Xnom, nom]=min(X) Xnom = -8 nom = 5
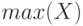 — находит максимальный элемент массива
— находит максимальный элемент массива  или при вызове вида
или при вызове вида ![[nomX, nom] = max(X)](/sites/default/files/tex_cache/2b9a417e0ec3ffab95bca93ea08a922b.png) определяет максимум и его номер.
определяет максимум и его номер.
>>> X=[-1 2 3 9 -8 7 5 ]; >>> max(X) ans = 9 >>> [ Xnom, nom]=max(X) Xnom = 9 nom = 4
 — определяет среднее арифметическое массива
— определяет среднее арифметическое массива  .
.
>>> X=[-1 2 3 9 -8 7 5 ]; >>> Sr= mean(X) Sr = 2.4286 >>> sum(X) / length (X) ans = 2.4286
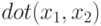 — вычисляет скалярное произведение векторов
— вычисляет скалярное произведение векторов  и
и 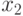 .
.
>>> x1 =[2 -3 0 5 1 ]; >>> x2 =[0 1 -2 3 -4]; >>> dot( x1, x2 ) ans = 8 >>> sum( x1 . * x2 ) ans = 8 >>> x1 = [ 2; - 3; 0 ]; x2 = [ 0; 1; - 2 ]; >>> dot( x1, x2 ) ans = -3 >>> sum( x1 . * x2 ) ans = -3
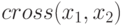 — вычисляет векторное произведение векторов
— вычисляет векторное произведение векторов  и
и 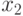 .
.
>>> x1 =[2 -3 0 ]; x2 =[0 1 -2]; >>> x=cross( x1, x2 ) x = 6 4 2 >>> x1 = [ 2; - 3; 0 ]; x2 = [ 0; 1; - 2 ]; >>> x=cross( x1, x2 ) x = 6 4 2
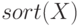 — выполняет сортировку массива
— выполняет сортировку массива  .
.
>>> X=[-1 2 3 9 -8 7 5 ]; >>> sort (X) % Сортировка по возрастанию ans = -8 -1 2 3 5 7 9 >>> -sort (-X) % Сортировка по убыванию ans = 9 7 5 3 2 -1 -8
5.4.2 Функции для работы c матрицами
![eye(n[, m])](/sites/default/files/tex_cache/41766ec48ce68a969d89eee97b75baa6.png) — возвращает единичную матрицу (вектор) соответствующей размерности.
— возвращает единичную матрицу (вектор) соответствующей размерности.
>>> eye( 4 ) ans = Diagonal Matrix 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 >>> eye( 2, 4 ) ans = Diagonal Matrix 1 0 0 0 0 1 0 0 >>> eye( 3, 1 ) ans = Diagonal Matrix 1 0 0 >>> eye( 1, 5 ) ans = Diagonal Matrix 1 0 0 0 0
![ones(n[, m, p, . . . ])](/sites/default/files/tex_cache/92e2c4bf945c02b9209f3d331bfee033.png) — формирует матрицу (вектор), состоящую из единиц.
— формирует матрицу (вектор), состоящую из единиц.
>>> ones( 2 ) ans = 1 1 1 1 >>> ones( 3, 3 ) ans = 1 1 1 1 1 1 1 1 1 >>> ones( 1, 4 ) ans = 1 1 1 1 >>> ones( 2, 1 ) ans = 1 1 >>> ones( 4, 2 ) ans = 1 1 1 1 1 1 1 1 >>> ones( 2, 3, 4 ) ans = ans ( :, :, 1 ) = 1 1 1 1 1 1 ans ( :, :, 2 ) = 1 1 1 1 1 1 ans ( :, :, 3 ) = 1 1 1 1 1 1 ans ( :, :, 4 ) = 1 1 1 1 1 1
![zeros(n[, m, p, . . . ])](/sites/default/files/tex_cache/0d091439de80e2d1e2072ca87e0ce00d.png) — возвращает нулевую матрицу (вектор) соответствующей размерности.
— возвращает нулевую матрицу (вектор) соответствующей размерности.
>>> zeros( 3 ) ans = 0 0 0 0 0 0 0 0 0 >>> zeros( 1, 1 ) ans = 0 >>> zeros( 1, 2 ) ans = 0 0 >>> zeros( 3, 2 ) ans = 0 0 0 0 0 0 >>> zeros( 4, 1 ) ans = 0 0 0 0 >>> zeros( 2, 2, 2 ) ans = ans ( :, :, 1 ) = 0 0 0 0 ans ( :, :, 2 ) = 0 0 0 0
![diag(X[, k])](/sites/default/files/tex_cache/8db51bde55a10b64b55ab3dd424913aa.png) — возвращает квадратную матрицу с элементами
— возвращает квадратную матрицу с элементами  на главной диагонали или на
на главной диагонали или на  –й. Функция
–й. Функция ![diag(M [, k])](/sites/default/files/tex_cache/c45c42926181c048861ad9a89212bfbf.png) , где
, где  — ранее определённая матрица, в качестве результата выдаст вектор столбец, содержащий элементы главной или
— ранее определённая матрица, в качестве результата выдаст вектор столбец, содержащий элементы главной или  –ой диагонали матрицы
–ой диагонали матрицы  .
.
>>> X=[-1 2 3 9 -8 7 5 ]; >>> diag(X) ans = Diagonal Matrix -1 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 -8 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 5 >>> diag(X, 0 ) ans = Diagonal Matrix -1 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 -8 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 5 >>> x =[2; -3; 0 ]; diag(X, 1 ) ans = 0 -1 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 0 -8 0 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 >>> diag( x, 1 ) ans = 0 2 0 0 0 0 -3 0 0 0 0 0 0 0 0 0 >>> x =[2; -3; 0 ]; >>> diag( x, 1 ) ans = 0 2 0 0 0 0 -3 0 0 0 0 0 0 0 0 0 >>> diag( x, -1) ans = 0 0 0 0 2 0 0 0 0 -3 0 0 0 0 0 0 >>> x =[2; -3; 1 ]; >>> diag( x, 1 ) ans = 0 2 0 0 0 0 -3 0 0 0 0 1 0 0 0 0 >>> diag( x, -1) ans = 0 0 0 0 2 0 0 0 0 -3 0 0 0 0 1 0 >>> diag( x, 2 ) ans = 0 0 2 0 0 0 0 0 -3 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 >>> diag( x, -2) ans = 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 -3 0 0 0 0 0 1 0 0 >>> M=[1 2 3; 4 5 6; 7 8 9 ] M = 1 2 3 4 5 6 7 8 9 >>> diag(M) ans = 1 5 9 >>> diag(M, 1 ) ans = 2 6 >>> diag(M, -1) ans = 4 8 >>> diag(M, 2 ) ans = 3 >>> diag(M, -2) ans = 7
![rand([n, m, p, . . . ])](/sites/default/files/tex_cache/9e88b64942ea4c226ab691cdeedb061d.png) — возвращает матрицу (вектор) с элементами распределёнными по равномерному закону,
— возвращает матрицу (вектор) с элементами распределёнными по равномерному закону,  без аргументов возвращает одно случайное число.
без аргументов возвращает одно случайное число.
>>> rand( 2 ) ans = 0.15907 0.80147 0.90460 0.40293 >>> rand( 3, 1 ) ans = 0.279005 0.031504 0.529279 >>> rand( 1, 4 ) ans = 0.85038 0.13899 0.50764 0.82887 >>> rand( 2, 5 ) ans = 0.782173 0.286649 0.563683 0.969862 0.708655 0.300415 0.545783 0.011614 0.143827 0.644821 >>> rand ans = 0.99252 >>> rand ans = 0.42848
![randn([n, m, p . . . ])](/sites/default/files/tex_cache/5d93f881f37491b9500618f62c861fb2.png) — возвращает матрицу (вектор), элементы которой являются числами, распределёнными по нормальному закону,
— возвращает матрицу (вектор), элементы которой являются числами, распределёнными по нормальному закону,  без аргументов возвращает одно случайно число.
без аргументов возвращает одно случайно число.
>>> randn( 2 ) ans = -1.04321 -1.81309 1.09223 -0.83071 >>> randn( 2, 4 ) ans = -0.222773 -0.540185 0.026355 0.308437 1.510429 1.360071 0.298315 1.186672 >>> randn( 1, 3 ) ans = 0.38577 -2.33667 -1.35689 >>> randn( 2, 1 ) ans = -0.66235 0.32907 >>> randn ans = -1.0607 >>> randn ans = -0.47825
![linspace(a, b[, n])](/sites/default/files/tex_cache/70ea8b12a080f681ea4c8ae31787580e.png) — возвращает массив из 100 (если
— возвращает массив из 100 (если  не указано) или из
не указано) или из  точек равномерно распределённых между значениями
точек равномерно распределённых между значениями  и
и  .
.
>>> linspace( a, b, 3 ) ans = -2 0 2 >>> a=-2;b=2;n=5; >>> linspace( a, b, n ) ans = -2 -1 0 1 2 >>> linspace( a, b, 3 ) ans = -2 0 2 >>> linspace( 0, 5 0, 5 ) ans = 0.00000 12.50000 25.00000 37.50000 50.00000
![logspace(a, b[, n])](/sites/default/files/tex_cache/45f38e377cb5d7f6478aa65d245f9553.png) — формирует массив из 50 (если
— формирует массив из 50 (если  не указано) или из
не указано) или из  точек, равномерно распределённых в логарифмическом масштабе между значениями
точек, равномерно распределённых в логарифмическом масштабе между значениями 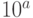 и
и 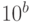 ; функция
; функция  даёт равномерное распределение из 50 точек в интервале от
даёт равномерное распределение из 50 точек в интервале от 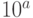 до
π4Обратите внимание, что это идёт в разрез с определением функции для произвольного
до
π4Обратите внимание, что это идёт в разрез с определением функции для произвольного , согласно которому интервал должен был бы быть от
, согласно которому интервал должен был бы быть от 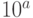 до
до 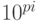 , сделано это для совместимости с соответствующей функцией matlab. (Прим. редактора )..
, сделано это для совместимости с соответствующей функцией matlab. (Прим. редактора )..
>>> logspace( 1, 2, 5 ) ans = 10.000 17.783 31.623 56.234 100.000 >>> logspace( 2, pi ) ans = Columns 1 through 7 : 100.0000 93.1815 86.8279 80.9075 75.3908 70.2503 65.4602 Columns 8 through 14 : 60.9968 56.8377 52.9622 49.3510 45.9860 42.8504 39.9287 Columns 15 through 21 : 37.2061 34.6692 32.3053 30.1025 28.0500 26.1374 24.3552 Columns 22 through 28 : 22.6945 21.1471 19.7052 18.3616 17.1096 15.9430 14.8559 Columns 29 through 35 : 13.8429 12.8991 12.0195 11.2000 10.436 39.724 79.0616 Columns 36 through 42 : 8.4438 7.8680 7.3315 6.8316 6.3658 5.9318 5.5273 Columns 43 through 49 : 5.1504 4.7992 4.4720 4.1671 3.8829 3.6182 3.3715 Column 50 : 3.1416
![repmat(M, n[, m])](/sites/default/files/tex_cache/faa7bb6c258ccfd6381a7b4daa3feaf7.png) — формирует матрицу состоящую
— формирует матрицу состоящую  или из
или из 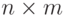 копий матрицы
копий матрицы  , если
, если  — скаляр, то формируется матрица, элементы которой равны значению
— скаляр, то формируется матрица, элементы которой равны значению  .
.
>>> M=[1 2 3; 4 5 6; 7 8 9 ]; >>> repmat(A, 2 ) ans = 3 -1 3 -1 6 -2 6 -2 3 -1 3 -1 6 -2 6 -2 >>> M=[1 2 3; 4 5 6; 7 8 9 ]; >>> repmat(M, 2 ) ans = 1 2 3 1 2 3 4 5 6 4 5 6 7 8 9 7 8 9 1 2 3 1 2 3 4 5 6 4 5 6 7 8 9 7 8 9 >>> repmat(M, 2, 3 ) ans = 1 2 3 1 2 3 1 2 3 4 5 6 4 5 6 4 5 6 7 8 9 7 8 9 7 8 9 1 2 3 1 2 3 1 2 3 4 5 6 4 5 6 4 5 6 7 8 9 7 8 9 7 8 9 >>> repmat(M, 3, 1 ) ans = 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 >>> repmat( 9, 3 ) ans = 9 9 9 9 9 9 9 9 9
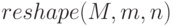 — возвращает матрицу размерностью
— возвращает матрицу размерностью  сформированную из матрицы
сформированную из матрицы  путём последовательной выборки по столбцам, если матрица
путём последовательной выборки по столбцам, если матрица  не имеет
не имеет  элементов, то выдаётся сообщение об ошибке.
элементов, то выдаётся сообщение об ошибке.
>>> M=[0 1 2 3; 4 5 6 7; 8 9 0 1 ] M = 0 1 2 3 4 5 6 7 8 9 0 1 >>> reshape(M, 3, 2 ) error: reshape: can ’ t reshape 3x4 array to 3x2 array >>> reshape(M, 3, 4 ) ans = 0 1 2 3 4 5 6 7 8 9 0 1 >>> reshape(M, 4, 3 ) ans = 0 5 0 4 9 3 8 2 7 1 6 1 >>> reshape(M, 2, 6 ) ans = 0 8 5 2 0 7 4 1 9 6 3 1 >>> reshape(M, 6, 2 ) ans = 0 2 4 6 8 0 1 3 5 7 9 1 >>> reshape(M, 1, 1 2 ) ans = 0 4 8 1 5 9 2 6 0 3 7 1 >>> reshape(M, 1 2, 1 ) ans = 0 4 8 1 5 9 2 6 0 3 7 1
![cat(n, A, B, [C, . . . ])](/sites/default/files/tex_cache/dcc6359edb46778866e483aec8cff9bc.png) — объединяет матрицы
— объединяет матрицы  и
и  или все входящие матрицы.
или все входящие матрицы.
>>> A=[0 1 2; 3 4 5; 6 7 8 ]; B=[11 12 13; 14 15 16; 17 18 19 ]; >>> cat ( 2,A,B) ans = 0 1 2 11 12 13 3 4 5 14 15 16 6 7 8 17 18 19 >>> [ A,B] ans = 0 1 2 11 12 13 3 4 5 14 15 16 6 7 8 17 18 19 >>> cat ( 1,A,B) ans = 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 19 >>> [A;B] ans = 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 19 >>> x1 =[2; -3; 0 ]; x2 = [ 0; 1; - 2 ]; >>> cat( 2, x1, x2 ) ans = 2 0 -3 1 0 -2 >>> cat( 1, x1, x2 ) ans = 2 -3 0 0 1 -2 >>> x1 =[2 -3 0 ]; x2 =[0 1 -2]; >>> cat( 2, x1, x2 ) ans = 2 -3 0 0 1 -2 >>> [ x1 x2 ] ans = 2 -3 0 0 1 -2 >>> cat( 1, x1, x2 ) ans = 2 -3 0 0 1 -2 >>> [ x1; x2 ] ans = 2 -3 0 0 1 -2
![rot90(M [, k])](/sites/default/files/tex_cache/504a8e1a24a78897ebfc1bb87c50fb7e.png) — осуществляет поворот матрицы
— осуществляет поворот матрицы  на 90 градусов против часовой стрелки или на величину
на 90 градусов против часовой стрелки или на величину 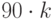 , где k — целое
число5Отрицательные значения k указывают на поворот по часовой стрелке, проверьте, что
, где k — целое
число5Отрицательные значения k указывают на поворот по часовой стрелке, проверьте, что 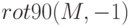 даст тот же результат, что и
даст тот же результат, что и  . (Прим. редактора)..
. (Прим. редактора)..
>>> M=[0 1 2 3; 4 5 6 7; 8 9 0 1 ] M = 0 1 2 3 4 5 6 7 8 9 0 1 >>> rot90(M) ans = 3 7 1 2 6 0 1 5 9 0 4 8 >>> rot90(M, 2 ) ans = 1 0 9 8 7 6 5 4 3 2 1 0 >>> rot90(M, 3 ) ans = 8 4 0 9 5 1 0 6 2 1 7 3
![tril(M [, k])](/sites/default/files/tex_cache/b07b23d7f759855d50865269aa62698d.png) — формирует из матрицы
— формирует из матрицы  нижнюю треугольную матрицу начиная с главной или с
нижнюю треугольную матрицу начиная с главной или с  –й диагонали.
–й диагонали.
>>> M=[0 1 2 3; 4 5 6 7; 8 9 0 1; 6 5 4 3 ]; >>> tril(M) ans = 0 0 0 0 4 5 0 0 8 9 0 0 6 5 4 3 >>> tril(M, 1 ) ans = 0 1 0 0 4 5 6 0 8 9 0 1 6 5 4 3 >>> tril(M, -1) ans = 0 0 0 0 4 0 0 0 8 9 0 0 6 5 4 0 >>> tril(M, 2 ) ans = 0 1 2 0 4 5 6 7 8 9 0 1 6 5 4 3 >>> tril(M, -2) ans = 0 0 0 0 0 0 0 0 8 0 0 0 6 5 0 0 >>> X=[-1 2 3 9 -8 7 5 ]; >>> tril(X) ans = -1 0 0 0 0 0 0 >>> tril(X’ ) ans = -1 2 3 9 -8 7 5
![triu(M [, k])](/sites/default/files/tex_cache/ae11269b8757b043311cf5d645f2e9c0.png) — формирует из матрицы
— формирует из матрицы  верхнюю треугольную матрицу начиная с главной или с
верхнюю треугольную матрицу начиная с главной или с  –й диагонали.
–й диагонали.
>>> M=[0 1 2 3; 4 5 6 7; 8 9 0 1; 6 5 4 3 ] M = 0 1 2 3 4 5 6 7 8 9 0 1 6 5 4 3 >>> triu(M) ans = 0 1 2 3 0 5 6 7 0 0 0 1 0 0 0 3 >>> triu(M, 1 ) ans = 0 1 2 3 0 0 6 7 0 0 0 1 0 0 0 0 >>> triu(M, -2) ans = 0 1 2 3 4 5 6 7 8 9 0 1 0 5 4 3 >>> triu(X) ans = -1 2 3 9 -8 7 5 >>> triu(X’ ) ans = -1 0 0 0 0 0 0
 — определяет число строк и столбцов матрицы
— определяет число строк и столбцов матрицы  , результатом её работы является вектор
, результатом её работы является вектор ![[n, m]](/sites/default/files/tex_cache/a7a1dadf662da11a6a88f967078d3fd0.png) .
.
>>> M=[0 1 2 3; 4 5 6 7; 8 9 0 1; 6 5 4 3 ]; >>> size(M) ans = 4 4 >>> X=[-1 2 3 9 -8 7 5 ]; >>> size(X) ans = 1 7 >>> size(X’ ) ans = 7 1 >>> eye( size (M) ) ans = Diagonal Matrix 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 >>> zeros( size (X) ) ans = 0 0 0 0 0 0 0
![prod(M [, k])](/sites/default/files/tex_cache/dedf12b460091884fc3e852f61297d6f.png) — формирует вектор–строку или вектор–столбец, в зависимости от значения
— формирует вектор–строку или вектор–столбец, в зависимости от значения  , каждый элемент которой является произведением элементов соответствующего столбца или строки матрицы
, каждый элемент которой является произведением элементов соответствующего столбца или строки матрицы  , если значение параметра
, если значение параметра  в конструкции отсутствует, то по умолчанию вычисляются произведения столбцов матрицы; понятно, что результатом работы функции
в конструкции отсутствует, то по умолчанию вычисляются произведения столбцов матрицы; понятно, что результатом работы функции  будет произведение всех элементов матрицы.
будет произведение всех элементов матрицы.
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ]; >>> prod(M) ans = 24 -25 32 18 >>> prod(M, 1 ) ans = 24 -25 32 18 >>> prod(M, 2 ) ans = 6 -40 -12 -120 >>> prod( prod (M) ) ans = -345600
![cumprod(M [, k])](/sites/default/files/tex_cache/518d748372f5bf645adcab1a797eebe4.png) — отличается от функции
— отличается от функции  тем, что операции описанные для неё применяются к строкам или к столбцам матрицы
тем, что операции описанные для неё применяются к строкам или к столбцам матрицы  , в зависимости от значения параметра
, в зависимости от значения параметра  , по умолчанию накапливание произведения выполняется по столбцам матрицы
, по умолчанию накапливание произведения выполняется по столбцам матрицы  .
.
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ]; >>> cumprod(M) ans = -1 1 -2 3 -4 5 2 6 -12 -5 8 6 24 -25 32 18 >>> cumprod(M, 1 ) ans = -1 1 -2 3 -4 5 2 6 -12 -5 8 6 24 -25 32 18 >>> cumprod(M, 2 ) ans = -1 -1 2 6 4 20 -20 -40 3 -3 -12 -12 -2 -10 -40 -120
![sum(M [, k])](/sites/default/files/tex_cache/84b38c84c5ff26af531449ce84c8780f.png) — формирует вектор–строку или вектор–столбец, в зависимости от значения
— формирует вектор–строку или вектор–столбец, в зависимости от значения  , каждый элемент которой является суммой элементов соответствующего столбца или строки матрицы
, каждый элемент которой является суммой элементов соответствующего столбца или строки матрицы  , если значение параметра
, если значение параметра  в конструкции отсутствует, то по умолчанию вычисляются суммы столбцов матрицы. Сумму всех элементов матрицы вычисляет функция
в конструкции отсутствует, то по умолчанию вычисляются суммы столбцов матрицы. Сумму всех элементов матрицы вычисляет функция  .
.
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ]; >>> sum(M) ans = 4 10 5 9 >>> sum(M, 1 ) ans = 4 10 5 9 >>> sum(M, 2 ) ans = 1 10 7 10 >>> sum(sum(M) ) ans = 28
![cumsum(M, [k])](/sites/default/files/tex_cache/235be4df19a988b4b383b887de62b87f.png) — отличается от функции
— отличается от функции  тем, что операции описанные для неё применяются либо к строкам либо к столбцам матрицы
тем, что операции описанные для неё применяются либо к строкам либо к столбцам матрицы  , в зависимости от значения параметра
, в зависимости от значения параметра  , по умолчанию результатом работы функции является матрица кумулятивных сумм столбцов матрицы
, по умолчанию результатом работы функции является матрица кумулятивных сумм столбцов матрицы  .
.
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ]; >>> cumsum(M) ans = -1 1 -2 3 3 6 -3 5 6 5 1 6 4 10 5 9 >>> cumsum(M, 1 ) ans = -1 1 -2 3 3 6 -3 5 6 5 1 6 4 10 5 9 >>> cumsum(M, 2 ) ans = -1 0 -2 1 4 9 8 10 3 2 6 7 -2 3 7 10
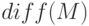 — из матрицы
— из матрицы  размерностью
размерностью  на
на  формирует матрицу размером
формирует матрицу размером  на
на  элементы которой представляют собой разность между элементами соседних строк
элементы которой представляют собой разность между элементами соседних строк  .
.
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ] M = -1 1 -2 3 4 5 -1 2 3 -1 4 1 -2 5 4 3 >>> diff(M) ans = 5 4 1 -1 -1 -6 5 -1 -5 6 0 2
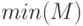 — формирует вектор-строку, каждый элемент которой является наименьшим элементом соответствующего столбца матрицы
— формирует вектор-строку, каждый элемент которой является наименьшим элементом соответствующего столбца матрицы  . Определить положение этих элементов в матрице можно, если вызвать функцию в формате
. Определить положение этих элементов в матрице можно, если вызвать функцию в формате ![[n, m] = min(M )](/sites/default/files/tex_cache/723dcdfa60134eb4cef0116af7aac25c.png) , где
, где  — это вектор минимальных элементов столбцов матрицы
— это вектор минимальных элементов столбцов матрицы  , а
, а  — вектор номеров строк матрицы
— вектор номеров строк матрицы  , в которых находятся эти элементы, конструкция
, в которых находятся эти элементы, конструкция 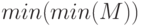 позволит отыскать минимум среди всех элементов матрицы.Вызов функции в виде
позволит отыскать минимум среди всех элементов матрицы.Вызов функции в виде ![min(M, [], k)](/sites/default/files/tex_cache/08fb2d9f80d8b5f763da8dc6d523279b.png) или
или ![[n, m] = min(M, [], k)](/sites/default/files/tex_cache/5da616e0447bcdcedfa8c3ab1d8f4a26.png) позволяет управлять направлением поиска, в частности можно отыскать минимальные элементы и их положение в строках матрицы
позволяет управлять направлением поиска, в частности можно отыскать минимальные элементы и их положение в строках матрицы  .И, наконец, функция
.И, наконец, функция  сформирует матрицу из строк
сформирует матрицу из строк 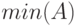 и
и 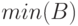 .
.
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ] M = -1 1 -2 3 4 5 -1 2 3 -1 4 1 -2 5 4 3 >>> min(M) ans = -2 -1 -2 1 >>> [ n,m]=min(M) n = -2 -1 -2 1 m = 4 3 1 3 >>> min(M’ ) ans = -2 -1 -1 -2 >>> [ n,m]=min(M’ ) n = -2 -1 -1 -2 m = 3 3 2 1 >>> min( min(M) )% Минимум среди всех элементов матрицы ans = -2 >>> [ n,m]=min( min(M) ) n = -2 m = 1 >>> min(M, [ ], 1 ) ans = -2 -1 -2 1 >>> min(M, [ ], 2 ) % Как и min(M) формирует вектор–строку, каждый элемент % которой равен минимальному элементу в соответствующем столбце M ans = -2 -1 -1 -2 >>> [ n,m]=min(M, [ ], 2 ) % Формирует вектор–столбец, каждый элемент % которого равен минимальному элементу в соответствующей строке матрицы % M и их положение в матрице — номера столбцов в которых они находятся. n = -2 -1 -1 -2 m = 3 3 2 1 >>> A=[0 1 2; 3 4 5; 6 7 8 ]; B=[11 12 13; 14 15 1 6; 17 18 19 ]; >>> min(A,B) ans = 0 1 2 % Первая строка — минимумы столбцов матрицы A, 3 4 5 % а вторая строка — матрицы B 6 7 8
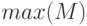 — формирует вектор-строку, каждый элемент которой является наибольшим элементом соответствующего столбца матрицы
— формирует вектор-строку, каждый элемент которой является наибольшим элементом соответствующего столбца матрицы  , действия функций
, действия функций ![[n, m] = max(M ), max(max(M )), max(M, [], k), [n, m] = max(A, [], k), max(A, B)](/sites/default/files/tex_cache/27cdc1d08f3ea2140838c36105c890e8.png) понятно из примеров:
понятно из примеров:
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ]; >>> max(M) ans = 4 5 4 3 >>> [ n,m]=max(M) n = 4 5 4 3 m = 2 2 3 1 >>> max(M’ ) ans = 3 5 4 5 >>> [ n,m]=max(M’ ) n = 3 5 4 5 m = 4 2 3 2 >>> max(max(M) ) ans = 5 >>> [ n,m]=max(max(M) ) n = 5 m = 2 >>> max(M, [ ], 1 ) ans = 4 5 4 3 >>> max(M, [ ], 2 ) ans = 3 5 4 5 >>> [ n,m]=max(M, [ ], 2 ) n = 3 5 4 5 m = 4 2 3 2 >>> A=[0 1 2; 3 4 5; 6 7 8 ]; B=[11 12 13; 14 15 1 6; 17 18 19 ]; >>> max(A,B) ans = 11 12 13 14 15 16 17 18 19
![mean(M, [k])](/sites/default/files/tex_cache/3c438250cdb5895a639ffc98ec1e4fec.png) — формирует вектор–строку или вектор–столбец, в зависимости от значения
— формирует вектор–строку или вектор–столбец, в зависимости от значения  , каждый элемент которого является средним значением элементов соответствующего столбца или строки матрицы
, каждый элемент которого является средним значением элементов соответствующего столбца или строки матрицы  , если значение параметра
, если значение параметра  в конструкции отсутствует, то по умолчанию вычисляются средние значения столбцов матрицы. Среднее всех элементов матрицы вычисляет функция
в конструкции отсутствует, то по умолчанию вычисляются средние значения столбцов матрицы. Среднее всех элементов матрицы вычисляет функция  .
.
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ]; >>> mean(M) ans = 1.0000 2.5000 1.2500 2.2500 >>> mean(M, 1 ) ans = 1.0000 2.5000 1.2500 2.2500 >>> mean(M, 2 ) ans = 0.25000 2.50000 1.75000 2.50000 >>> mean(mean(M) ) ans = 1.7500
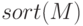 — выдаёт матрицу того же размера, что и
— выдаёт матрицу того же размера, что и  , каждый столбец которой упорядочен по возрастанию.
, каждый столбец которой упорядочен по возрастанию.
>>> M=[-1 1 -2 3; 4 5 -1 2; 3 -1 4 1; -2 5 4 3 ] M = -1 1 -2 3 4 5 -1 2 3 -1 4 1 -2 5 4 3 >>> sort (M) ans = -2 -1 -2 1 -1 1 -1 2 3 5 4 3 4 5 4 3 >>> sort (M’ ) ans = -2 -1 -1 -2 -1 2 1 3 1 4 3 4 3 5 4 5 >>> -sort (- M) ans = 4 5 4 3 3 5 4 3 -1 1 -1 2 -2 -1 -2 1 >>> -sort (-M’ ) ans = 3 5 4 5 1 4 3 4 -1 2 1 3 -2 -1 -1 -2
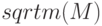 — относится к так называемым матричным функциям и возвращает матрицу
— относится к так называемым матричным функциям и возвращает матрицу  , для которой
, для которой 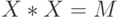 (матрица
(матрица  должна быть квадратной).
должна быть квадратной).
>>> A=[1 0 -3;0 1 2; 2 0 -1] A = 1 0 -3 0 1 2 2 0 -1 >>> X=sqrtm (A) X = 1.53024 0.00000 -1.41861 -0.35349 1.00000 0.94574 0.94574 0.00000 0.58450 >>> X*X % Проверка ans = 1.00000 0.00000 -3.00000 0.00000 1.00000 2.00000 2.00000 0.00000 -1.00000 >>> Y=sqrt (A)% Извлечение квадратного корня из элементов матрицы A Y = 1.00000 + 0.00000i 0.00000 + 0.00000i 0.00000 + 1.73205i 0.00000 + 0.00000i 1.00000 + 0.00000i 1.41421 + 0.00000i 1.41421 + 0.00000i 0.00000 + 0.00000i 0.00000 + 1.00000 i % sqrtm(A) и sqrt(A) дают различные результаты >>> Y*Y % Матричное умножение ans = 1.00000 + 2.44949i 0.00000 + 0.00000i -1.73205 + 1.73205i 2.00000 + 0.00000i 1.00000 + 0.00000i 1.41421 + 1.41421i 1.41421 + 1.41421i 0.00000 + 0.00000i -1.00000 + 2.44949i >>> Y. *Y % Поэлементное умножение ans = 1.00000 0.00000 -3.00000 0.00000 1.00000 2.00000 2.00000 0.00000 -1.00000
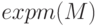 и
и 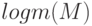 — взаимообратные матричные функции, первая вычисляет матричную экспоненту
— взаимообратные матричные функции, первая вычисляет матричную экспоненту 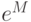 , а вторая выполняет логарифмирование по основанию
, а вторая выполняет логарифмирование по основанию  .
.
>>> A=[1 0 -3;0 1 2; 2 0 -1];B= expm(A) B = -0.26543 0.00000 -1.05553 1.98914 2.71828 0.70369 0.70369 0.00000 -0.96912 >>> logm(B) ans = 1.00000 + 0.00000i 0.00000 + 0.00000i -3.00000 - 0.00000i -0.00000 - 0.00000i 1.00000 + 0.00000i 2.00000 + 0.00000i 2.00000 + 0.00000i 0.00000 + 0.00000i -1.00000 - 0.00000i
