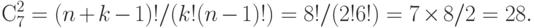|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2. |
Сочетания
Любое подмножество из  элементов множества
элементов множества  , содержащего
, содержащего  элементов, называется сочетанием
элементов, называется сочетанием 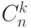 из
из  элементов по
элементов по  . Сочетания различаются компонентами .
. Сочетания различаются компонентами .
Примечание. Если объединить все размещения из  элементов по
элементов по  , состоящие из одних и тех же элементов (не учитывая расположения) в классы эквивалентности, то каждому классу будет соответствовать ровно одно сочетание
, состоящие из одних и тех же элементов (не учитывая расположения) в классы эквивалентности, то каждому классу будет соответствовать ровно одно сочетание 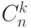 и наоборот:
и наоборот:
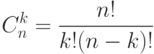
Пример. Для множества 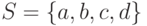 из предыдущего примера число различных двухэлементных сочетаний
из предыдущего примера число различных двухэлементных сочетаний 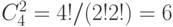 .
.
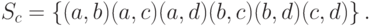
Задача. Сколько различных комбинаций может выпасть в спортлото "5 из 36":
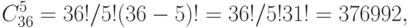
а в спортлото "6 из 45" -  .
.
Сочетания с повторениями
Сочетаниями из  элементов по
элементов по  элементов с повторениями называются группы, содержащие
элементов с повторениями называются группы, содержащие  элементов, причем каждый элемент принадлежит к одному из
элементов, причем каждый элемент принадлежит к одному из  типов.
типов.
Например. Для множества 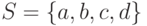 двухэлементные сочетания с повторениями
двухэлементные сочетания с повторениями 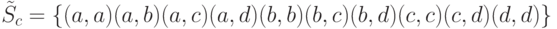 .
.
Число различных сочетаний из  элементов по
элементов по  c повторениями равно
c повторениями равно
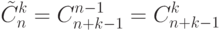
Пример. Кости домино можно рассматривать как цифры 0, 1, 2, 3, 4, 5, 6. Число сочетаний по два элемента равно