Теория множеств

Начальные сведения о множествах

Одним из основных исходных понятий математики является понятие множества и его элементов. Основатель теории множеств Кантор дал такую трактовку: "Под множеством понимают объединение в одно общее объектов, хорошо различимых нашей интуицией или нашей мыслью".

Понятие множества как и любое другое исходное понятие не имеет строгого математически точного описания. Можно дать следующее определение.

" Множество - это совокупность определенных различаемых объектов, причем таких, что для каждого можно установить, принадлежит этот объект данному множеству или нет."

Как правило, элементы множества обозначаются маленькими буквами, а сами множества - большими. Принадлежность элемента множеству обозначается так: , где знак 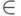является стилизацией первой буквы греческого слова (есть, быть), знак непринадлежности - .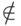

Множества могут быть конечными, бесконечными и пустыми. Множество, содержащее конечное число элементов, называется конечным. Если множество не содержит ни одного элемента, то оно называется пустым и обозначается . Например:

- множество студентов потока 99ПС - конечное множество ;

- множество звезд во Вселенной - бесконечное множество ;

- множество студентов потока 98СП, хорошо знающих три иностранных языка (японский, китайский и французский), видимо, пустое множество.

Множество называют подмножеством множества (обозначается ), если всякий элемент множества является элементом множества : ( рис. 1.1).

Рис. 1.1.

При этом говорят, что содержит , или покрывает . Невключение подмножества в множество обозначается так: .

Множества и равны ( ) тогда и только тогда, когда , и , т. е. элементы множеств и совпадают.

Множество называется собственным подмножеством множества , если , а . Обозначается так: .

Например: .

Мощностью конечного множества называется число его элементов. Обозначается . Например, , .

Принято считать, что пустое множество является подмножеством любого множества. Множество может обладать иерархической структурой. В этом случае говорят о семействе множества или булеане.

Семейством множества или булеаном является множество, элементами которого являются всевозможные подмножества множества .

Например,

В общем случае мощность булеана .

Универсальным множеством называется множество всех рассматриваемых в данной задаче элементов.

Способы задания множеств

Множества могут быть заданы списком, порождающей процедурой, арифметическими операциями, описанием свойств элементов или графическим представлением.

1. Задание множеств списком предполагает перечисление элементов. Например, множество состоит из букв или множество включает цифры .

   Пример: .

2. Задание множеств порождающей процедурой или арифметическими операциями означает описание характеристических свойств элементов множества: , т. е. множество содержит такие элементы , которые обладают свойством .

   Например:

   • , - множество всех натуральных чисел;
   • . или ;
   • .

3. Задание множества описанием свойств элементов: например, - это множество чисел, являющихся степенями двойки.

   К описанию свойств естественно предъявить требования точности и недвусмысленности. Так, " множество всех хороших песен 2003 года" каждый составит по-разному. Надежным способом однозначного задания множества является использование разрешающей процедуры, которая для любого объекта устанавливает, обладает ли он данным свойством и соответственно является ли элементом рассматриваемого множества.

   Например, - множество успевающих студентов. Разрешающей процедурой включения в множество является отсутствие неудовлетворительных оценок в последней сессии.

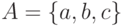4. Графическое задание множеств происходит с помощью диаграмм Эйлера-Венна. Замкнутая линия-круг Эйлера - ограничивает множество, а рамка - универсальное пространство ( рис. 1.2). Заданы два множества: и . Если элементов множеств немного, то они могут на диаграмме указываться явно.

   

   
   Рис. 1.2.