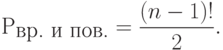|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2. |
Комбинаторика
Комбинаторика - один из разделов дискретной математики, который приобрел важное значение в связи с использованием его в ВТ, кибернетике, робототехнике. Большинство задач комбинаторики можно сформулировать как задачи теории конечных множеств, поэтому эти две темы - элементы теории множеств и комбинаторика - рассматриваются взаимосвязано.
Человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. Например, сколькими способами могли быть распределены золотая, серебряная и бронзовая медали на Олимпийских играх в Сеуле по баскетболу; или сколькими различными способами можно разместить здания на площади? Задачи такого типа называются комбинаторными.
С комбинаторными вычислениями приходится иметь дело представителям многих специальностей: ученому-химику при рассмотрении различных возможных типов связи атомов в молекулах, биологу - при изучении возможных последовательностей чередования аминокислот в белковых соединениях, диспетчеру - при составлении графика движения и т. д.
Комбинаторика возникла в XVI веке. В то время в жизни привилегированных слоев общества большое место занимали азартные игры (карты, кости). Были широко распространены лотереи. Возникали вопросы: сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей? Эти и другие проблемы оказались движущей силой в развитии комбинаторики.
Теоретические исследования вопросов комбинаторики предприняли Паскаль и Ферма, Бернулли, Лейбниц и Эйлер и др.
Для инженерных специальностей университета комбинаторные задачи приходится решать в следующих случаях:
- при конструировании:
- синтезе схем и проектирования:
- при решении вопроса, какой набор стандартных микросхем выбрать, чтобы реализовать разработанную схему устройства;
- при разработке схемы на подсхемы для реализации различными блоками и т. д.;
- при контроле, выбирая-перебирая последовательность тестирующих сигналов;
- в организации систем, решая вопрос, каким выбрать оптимальный маршрут передачи информации по сети и т. п.
Общие правила комбинаторики
Рассмотрим некоторые конкретные задачи.
Задача. 1. "Суеверные велосипедисты"
"Опять восьмерка" - воскликнул председатель клуба велосипедистов, - а все потому, что у меня билет № 008. Надо менять номера и проводить перерегистрацию".
Итак, сколько членов было в клубе, если известно, что использованы все трехзначные номера, не содержащие ни одной цифры 8?
| 00 | 01 | 02 | .................... | 09 |
|---|---|---|---|---|
| 10 | 11 | 12 | .................... | 19 |
| 20 | 21 | 22 | .................... | 29 |
| 30 | 31 | 32 | .................... | 39 |
| 40 | . | . | .................... | . |
| 50 | . | . | .................... | . |
| 60 | . | . | .................... | . |
| 70 | . | . | .................... | . |
| 80 | . | . | .................... | . |
| 90 | . | . | .................... | . |
Для решения этой задачи определим сначала, сколько однозначных номеров не содержит цифру 8? Это 0, 1, 2, 3, 4, 5, 6, 7, 9 - всего девять цифр, а теперь найдем все двузначные номера: их 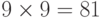 (таблица). За каждым двузначным номером можно поставить любую допустимую цифру, следовательно,
(таблица). За каждым двузначным номером можно поставить любую допустимую цифру, следовательно, 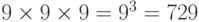 . Значит в клубе было 729 велосипедистов.
. Значит в клубе было 729 велосипедистов.
В другом клубе велосипедисты были ещё суевернее и решили, что цифра 0 тоже похоже на вытянутое колесо и они отказались от этой цифры .
Сколько членов было в клубе, если номера билетов были трехзначными и не включали цифр 0 и 8? 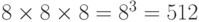 .
.
Задача 2. "Секретный замок"
В сейфах применяют секретные замки, которые открываются, когда набран шифр. Этот шифр набирают с помощью одного или нескольких дисков. Пусть на диск нанесены 12 букв, а секретное слово-шифр состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим шифра?
Всего попыток 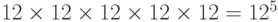 , одна из которых удачная, следовательно неудачных попыток
, одна из которых удачная, следовательно неудачных попыток 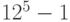 .
.
Задача 3. "Команда космического корабля"
В случае, когда число возможных выборов на каждом шаге зависит от того какие элементы были выбраны ранее, удобно решение изображать в виде "дерева". Сначала из одной точки проводят столько отрезков, сколько различных выборов можно сделать на 1-м шаге. Из конца каждого отрезка проводят столько отрезков, сколько можно сделать на 2-м шаге и т. д. В результате получается "дерево решений".
Рассмотрим задачу о формировании команды космического корабля. Известно, что возникнет вопрос психологической совместимости. Предположим, надо составить команду из 3-х человек: командира, инженера и врача. На место командира есть четыре кандидата: 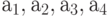 , на место инженера три -
, на место инженера три - 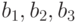 , на место врача три -
, на место врача три - 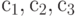 . Проведенная проверка показала, что
. Проведенная проверка показала, что  совместим с
совместим с 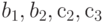 ;
; 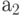 совместим с
совместим с 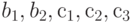 ;
; 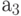 совместим с
совместим с 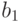 и
и 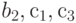 ;
;  совместим с
совместим с 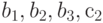 ;
; 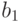 не совместим с
не совместим с 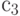 ;
; 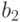 не совместим с
не совместим с 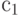 ;
; 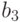 не совместим с
не совместим с 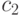 .
.
Сколькими способами при этих условиях может быть составлена команда корабля? По результатам совместимости строится дерево решений (
рис.
5.1). Итак, всего 11 комбинаций, а без ограничения 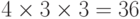 .
.
Упорядоченные множества. Перестановки
Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число (номер элемента) от  до
до 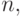 где
где  - число элементов множества.
- число элементов множества.
Всякое конечное множество можно сделать упорядоченным, если, например, переписать все элементы множества в некоторый список ( 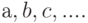 .), а затем каждому элементу присвоить номер.
.), а затем каждому элементу присвоить номер.
Упорядоченные множества считаются различными, если они отличаются либо своими элементами, либо их порядком.
Различные упорядоченные множества, которые отличаются лишь порядком элементов, называются перестановками этого множества.
Пример. Перестановки множества 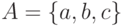 из 3-х элементов имеют вид
из 3-х элементов имеют вид 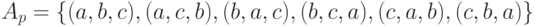 .
.
Число перестановок из  элементов
элементов 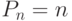 !
!
Задача 1. Сколькими способами можно разместить на плате 4 элемента? 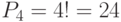 .
.
Задача 2. Сколькими способами можно выстроить в линейку 10 человек (5 девушек и 5 юношей) с условием, чтобы девушки и юноши чередовались, первая - девушка? 5 девушек можно разместить 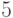 ! способами, а 5 юношей аналогично
! способами, а 5 юношей аналогично 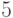 !. Следовательно, всего способов
!. Следовательно, всего способов  .
.
Перестановка с повторением
Если рассматривать упорядоченные  -элементные наборы из множества
-элементные наборы из множества  , которые состоят не только из различных элементов множества
, которые состоят не только из различных элементов множества  , но содержат некоторые повторяющиеся элементы, то получим перестановки с повторением.
, но содержат некоторые повторяющиеся элементы, то получим перестановки с повторением.
Пусть 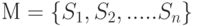 - множество из
- множество из  элементов и
элементов и 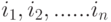 - натуральные числа, такие, что их сумма равна
- натуральные числа, такие, что их сумма равна  , а
, а 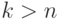 .
.
Каждый упорядоченный набор  элементов
элементов 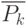 содержащий элемент
содержащий элемент 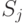 ровно
ровно 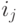 раз (
раз ( 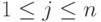 ) называется перестановками множества
) называется перестановками множества  с повторением:
с повторением:
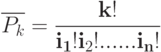
Примечание: при 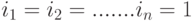 получим перестановки множества из
получим перестановки множества из  элементов без повторений.
элементов без повторений.
Пример. Сколько различных шестизначных чисел можно составить из цифр 1, 1, 1, 5, 5, 9? Подставим в формулу  различных шестизначных чисел.
различных шестизначных чисел.
Задача 2. Сколько различных слов можно получить, переставляя буквы слова "математика"?

Перестановки предметов, расположенных в круг
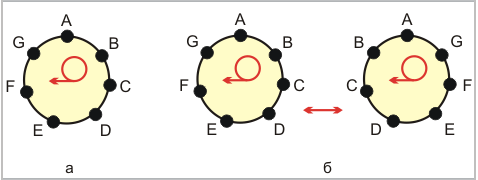
Задача 1. "Хоровод". Семь девушек водят хоровод. Сколькими различными способами они могут встать в круг (рис. 5.2,а)?
Если бы они стояли на месте, то количество способов - 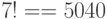 . Но так как танцующие кружатся, то их положение относительно окружающих не имеет роли, следовательно, важно лишь взаимное расположение. Поэтому перестановки, переходящие друг в друга, надо считать одинаковыми. Но из каждой перестановки можно получить еще 6 путем вращения - 7 мест:
. Но так как танцующие кружатся, то их положение относительно окружающих не имеет роли, следовательно, важно лишь взаимное расположение. Поэтому перестановки, переходящие друг в друга, надо считать одинаковыми. Но из каждой перестановки можно получить еще 6 путем вращения - 7 мест: 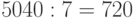 различных перестановок девушек в хороводе.
различных перестановок девушек в хороводе.
В общем случае, если рассматривать  предметов, расположенных в круг, и считать одинаковыми расположения, переходящие друг в друга при вращении, то число различных перестановок равно
предметов, расположенных в круг, и считать одинаковыми расположения, переходящие друг в друга при вращении, то число различных перестановок равно
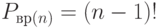
Задача 2. Сколько ожерелий можно составить из 7 бусинок?
По аналогии с предыдущей задачей можно подумать, что 720. Но ожерелье можно не только вращать, но и перевернуть
(рис. 5.2,б). Поэтому ответ 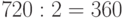 , т. е.
, т. е.