|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2. |
Свойства отношений
Пусть 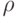 - отношение на множестве
- отношение на множестве  .
.
Тогда
в) 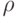 транзитивно, если
транзитивно, если 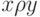 и
и 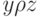 влечет
влечет 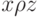 ;
;
г) 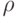 антисимметрично, если
антисимметрично, если 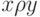 и
и 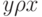 влекут
влекут 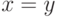 .
.
Пример 1. Пусть 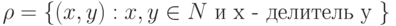 ,
, 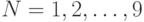 .
.
В явном виде
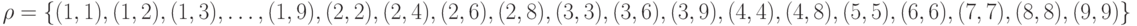
Тогда 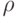
-
рефлексивно, так как
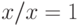 для всех
для всех 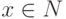 ;
; - несимметрично, поскольку 2 - делитель 4, то 4 не является делителем 2;
- транзитивно, так как (2, 4) и (4, 8) влечет (2, 8);
-
антисимметрично, так как если
 и
и  , то
, то 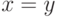 .
.
Пример 2. Пусть 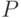 - множество всех людей,
- множество всех людей,  и
и  определяются cледующим образом:
определяются cледующим образом:  .
.
Очевидно, что  транзитивно, а
транзитивно, а  рефлексивно, симметрично и транзитивно.
рефлексивно, симметрично и транзитивно.
Пример 3. Пусть 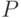 - множество всех людей. Определим отношение
- множество всех людей. Определим отношение  такое, что
такое, что 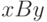 тогда и только тогда, когда
тогда и только тогда, когда  является братом
является братом  .
.  (
рис.
4.1).
(
рис.
4.1).
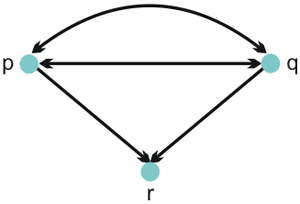
В семье, состоящей из двух братьев  и
и  и сестры
и сестры  , имеем ситуацию: отношение
, имеем ситуацию: отношение  не симметрично, так как
не симметрично, так как  , но не
, но не 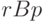 ;
;  не антисимметрично, так как
не антисимметрично, так как  и
и 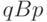 , хотя и
, хотя и  и
и  различны.
различны.
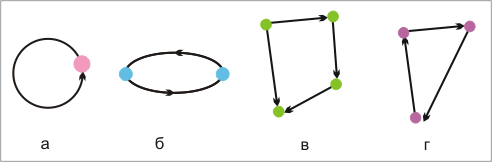
В более общей ситуации мы можем интерпретировать рассмотренные выше характеристики отношений путем построения диаграмм:
a) отношение рефлексивно тогда и только тогда, когда для каждого узла на диаграмме существует стрелка-петля;
б) отношение симметрично тогда и только тогда, когда для каждой стрелки, соединяющей два узла, существует также стрелка, соединяющая два этих узла в обратном направлении.
в) отношение транзитивно тогда и только тогда, когда для каждой пары узлов  и
и  , связанных последовательностью стрелок от
, связанных последовательностью стрелок от  к
к 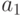 и от
и от 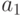 к
к 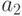 ..., от
..., от 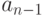 к
к 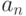 , от
, от 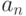 к
к  , существуют также стрелки от
, существуют также стрелки от  к
к  .
.
г) отношение антисимметрично тогда и только тогда, когда не существует двух различных узлов, связанных парой стрелок ( рис. 4.2).
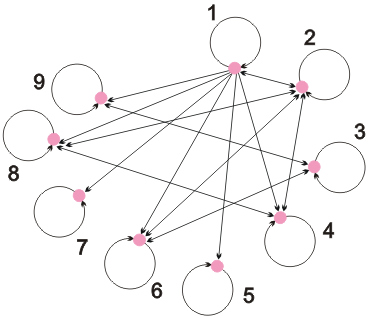
Для примера 1 (
рис.
4.3)  .
.
В явном виде
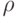
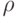 рефлексивно, несимметрично, транзитивно и антисимметрично.
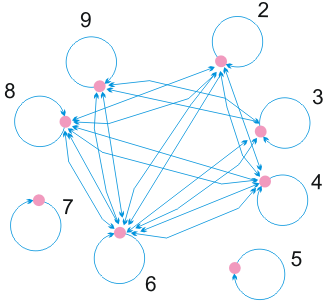
рефлексивно, несимметрично, транзитивно и антисимметрично.Пример 4 (
рис.
4.4). 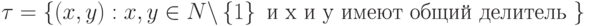 ,
,  = {(2, 2), (2, 4), (2, 6), (2, 8), (3, 3), (3, 6), (3, 9), (4, 4), (4, 8), (4, 6), (5, 5),
(6, 3), (6, 2), (6, 6), (7, 7), (8, 2), (8, 4), (9, 3), (9, 9), (6, 4), (8, 6), (6, 8), (9, 6), (6, 9)} .
= {(2, 2), (2, 4), (2, 6), (2, 8), (3, 3), (3, 6), (3, 9), (4, 4), (4, 8), (4, 6), (5, 5),
(6, 3), (6, 2), (6, 6), (7, 7), (8, 2), (8, 4), (9, 3), (9, 9), (6, 4), (8, 6), (6, 8), (9, 6), (6, 9)} .
Отношение  рефлексивно, симметрично, но не транзитивно и антисимметрично.
рефлексивно, симметрично, но не транзитивно и антисимметрично.

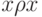 для
для 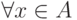 ;
;