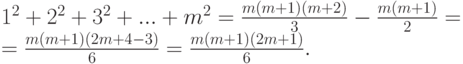Введение в теорию множеств и комбинаторику
[+]
Вятский государственный университет
Опубликован: 21.03.2008 | Доступ: свободный | Студентов: 2166 / 536 | Оценка: 4.39 / 4.31 | Длительность: 06:24:00
Тема: Алгоритмы и дискретные структуры
Специальности: Программист, Математик
Теги: beta, алгебра, арифметическая операция, делитель, законы, книги, комбинаторика, пересечение, перестановка, подмножество, проекция, разность, формула включения-исключения, шифр, элемент множества, элементы
Лекция 6:

Сочетания
A
|
версия для печати
< Лекция 5 || Лекция 6: 123 || Лекция 7 >

Сумма степенных рядов

Перепишем формулу (6.7).

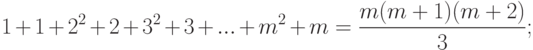
1 + 1 + 2^2 + 2 + 3^2 + 3 + ... + m^2 + m = \frac{{m(m + 1)(m + 2)}}{3};
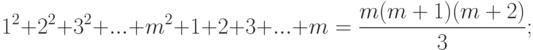
1^2 + 2^2 + 3^2 + ... + m^2 + 1 + 2 + 3 + ... + m = \frac{{m(m + 1)(m + 2)}}{3};

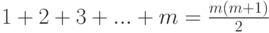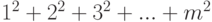Зная, что 1 + 2 + 3 + ... + m = \frac{{m(m + 1)}}{2}, а ( 1^2 + 2^2 + 3^2 + ... + m^2 ) - это искомое выражение, тогда

\begin{array}{l} 1^2 + 2^2 + 3^2 + ... + m^2 = \frac{{m(m + 1)(m + 2)}}{3} - \frac{{m(m + 1)}}{2} = \\ = \frac{{m(m + 1)(2m + 4 - 3)}}{6} = \frac{{m(m + 1)(2m + 1)}}{6}. \\ \end{array} ( 6.9)

Аналогично, используя формулу (6.8), можно найти сумму кубов:

\boxed{1^3 + 2^3 + ... + m^3 = \frac{{m^2 (m + 1)^2 }}{4}}. ( 6.10)
6 + 24 + 60 + 120 + ... + m(m + 1)(m + 2) = \frac{{m(m + 1)(m + 2)(m + 3)}}{4};
2^3 - 2 + 3^3 - 3 + 4^3 - 4 + 5^3 - 5 + ... + (m + 1)^3 - (m + 1) = \frac{{m(m + 1)(m + 2)(m + 3)}}{4};
1^3 + 2^3 + 3^3 + 4^3 + 5^3 + ... + (m + 1)^3 - (1 + 2 + 3 + 4 + 5 + ... + m + 1) = \frac{{m(m + 1)(m + 2)(m + 3)}}{4};
\begin{array}{l} 1^3 + 2^3 + 3^3 + 4^3 + 5^3 + ... + m^3 = \frac{{m(m + 1)(m + 2)(m + 3)}}{4} + \frac{{m(m + 1)(m + 2)}}{2} - \frac{{(m + 1)^3 }}{3} = \\ = (m^4 + 3m^3 + 2m^2 + 3m^3 + 9m^2 + 6m + 2m^2 + 6m + 4 - 4m^3 - - 12 m^2 - 12m - 4) = \\ (m^4 + 2m^3 + m^2)/4 = m^2 (m^2 + 2m + 1)/4 = \frac{{m^2 (m + 1)^2 }}{4}. \\ \end{array}
Дальше >>
< Лекция 5 || Лекция 6: 123 || Лекция 7 >

Вопросы и ответы

вопросов: 1
Владислав Бариков
Владислав Бариков

Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2.​

ответить