Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.10.2007 | Доступ: свободный | Студентов: 4540 / 789 | Оценка: 4.09 / 3.28 | Длительность: 11:25:00

Тема: Математика

Специальности: Математик

Теги: линейные пространства, метод Гауса, определители, векторы, матрицы

|

Вам нравится? Нравится 45 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Лекция 10:

Подпространства линейного пространства. Евклидово пространство. Линейные преобразования в линейном пространстве. Представление линейного преобразования матрицей. Действия над линейными преобразованиями. Примеры линейных преобразований

A

|

версия для печати

Примеры линейных преобразований

Пример 1. Пусть преобразование А есть поворот всех векторов 0Х плоскости х0y, т.е. поворот плоскости х0y вокруг начала координат на угол $\phi$ против часовой стрелки. Это преобразование линейно, так как безразлично, сначала ли сложить векторы а и b, а потом повернуть их на угол $\phi$ , или сначала повернуть векторы на указанный угол, а потом сложить их (рис. 9.1, а).

Рис. 9.1.

Так же будет безразлично умножить ли сначала вектор а на число $\lambda$ , а затем повернуть его на угол $\phi$ , или сделать это в обратном порядке (рис. 9.1, б).

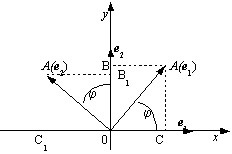
Чтобы построить матрицу рассматриваемого линейного преобразования - поворота на угол $\phi$ , выберем в рассматриваемом евклидовом пространстве V₂ базис из двух единичных взаимноперпендикулярных векторов е₁ и е₂. Вектор е₁ после поворота на угол $\phi$ перейдет в вектор А(е₁), который также будет являться единичным и образовывать с исходным вектором е₁ угол $\phi$ , а с вектором е₂ угол $\pi /2 - \varphi$ (рис. 9.2). Из (рис. 9.2) очевидно, что

$A(e_1)=OC+OB=\alpha e_1+\beta e_2.$

( 9.16)

Но $\alpha = |ОС| = |А(е_{1})| \cos \varphi = 1 \times \cos \varphi ; \ \beta = |ОB| = |А(е_{1})| \cos (\pi /2 - \varphi ) = |А(е_{1})| \sin \varphi = 1 \times \sin \varphi$ . Тогда, подставив полученные значения $\alpha$ и $\beta$ в равенство (9.16), получим

$A(e_1)=\cos\varphi\cdot e_1+\sin\varphi\cdot e_2.$

( 9.17)

Аналогично рассуждая, из рис. 9.2 можно получить формулы преобразования для вектора А(е₂):

$A(e_2)=OC_1+OB_1=\alpha_1 e_1 + \beta_1 e_2.$

( 9.18)

Рис. 9.2.

Но $\alpha _{1} = -|ОС_{1}| = -|А(е_{2})| \sin (\pi /2+\varphi ) = -1 \times \sin \varphi ; \beta _{1}= |ОB_{1}| = |А(е_{2})|\cos \varphi = 1 \times \cos\varphi$ . Тогда, подставив полученные значения $\alpha _{1} и \beta _{1}$ в равенство (9.18), будем иметь

$А(е_1) = -\sin\varphi\times е_1 + \cos\varphi \times е_2.$

( 9.19)

Из равенств (9.17) и (9.19) найдем матрицу

$A'= \begin{pmatrix} \cos\varphi & \sin\varphi \\ -\sin\varphi & \cos\varphi \end{pmatrix},$

, выражающую образы базисных векторов через сами базисные векторы [см. формулe (9.13)]. Тогда матрица А, задающая линейное преобразование в данном пространстве V₂, есть $A= \begin{pmatrix} \cos\varphi & -\sin\varphi \\ \sin\varphi & \cos\varphi \end{pmatrix} .$

Пример 2. Пусть в пространстве V₂ каждому вектору х ставится в соответствие вектор у = А(х), представляющий собой зеркальное отображение вектора х относительно некоторой фиксированной прямой 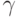$\gamma$ , проходящей через точку 0, которая принимается за начало всех векторов $х \in V_{2}$ (рис. 9.3). 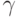Преобразование А в этом случае является линейным и называется зеркальным отображением относительно прямой $\gamma$ . Примем за базис два единичных взаимно ортогональных вектора (рис. 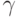9.4), один из которых направим по прямой $\gamma$ . Найдем матрицу этого преобразования. Базисный вектор е₁ преобразуется в вектор А(е₁) = е₁, а вектор е₂ - в вектор А(е₂) = -е₂, т.е. А(е₁) = е₁ = 1 x е₁+0xе₂, А(е₂) = -е₂ = 0xе₁ + (-1)xе₂. Тогда в выбранном базисе матрицы A' и А имеют вид:

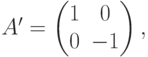
$A'= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix},$

$A= \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}.$

Рис. 9.3.

Рис. 9.4.

Пример 3. Определим линейное преобразование А, переводящее каждый вектор $х \in R_{n}$ в $\lambda х \in R_{n}$ , где $\lambda$ - фиксированное число из поля К, т.е. $\forall х \in R_{n} \exists \lambda х \in R_{n}$ , которое называется преобразованием подобия. Найдем его матрицу. Для базисных векторов е₁, е₂, ..., е_n имеем

$\begin{gathered} A(e_1)=\lambda e_1 = \lambda e_1 + 0e_2 + \ldots + 0e_n; \\ A(e_2)=\lambda e_2 = 0e_1 + \lambda e_2 + \ldots + 0e_n; \\ \ldots \\ A(e_n)=\lambda e_n = 0e_1 + 0e_2 + \ldots + \lambda e_n. \end{gathered}$

Тогда

$A'=A= \begin{pmatrix} \lambda & 0 & \ldots & 0 \\ 0 & \lambda & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & \lambda \end{pmatrix}.$

Пример 4. Если $\forall х \in R_{n}$ преобразование А переводит вектор х сам в себя А(х) = х, то такое преобразование тоже линейно, называется тождественным и обозначается Е

$\begin{gathered} A(e_1)=e_1=1\times e_1+0e_2+\ldots+0e_n; \\ A(e_2)=e_2=0e_1+1\times e_2+\ldots+0e_n; \\ \ldots \\ A(e_1)=e_1=0e_1+0e_2+\ldots+1\times e_n. \end{gathered}$

Таким образом, матрица тождественного преобразования Е в любом базисе есть единичная матрица

$A'=A=E= \begin{pmatrix} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & 1 \end{pmatrix}.$

Пример 5. Если $\forall х \in R_{n}$ преобразование А переводит вектор х в нулевой А(х) = 0, то такое преобразование является линейным и называется нулевым.

$\begin{gathered} A(e_1)=0e_1=0e_1+0e_2+\ldots+0e_n; \\ A(e_2)=0e_2=0e_1+0e_2+\ldots+0e_n; \\ \ldots \\ A(e_n)=0e_n=0e_1+0e_2+\ldots+0e_n. \end{gathered}$

Матрица нулевого преобразования в любом базисе есть нулевая матрица V:

$V= \begin{pmatrix} 0 & 0 & \ldots & 0 \\ 0 & 0 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & 0 \end{pmatrix}.$

Дальше >>

Введение в линейную алгебру

Примеры линейных преобразований

Вопросы и ответы

Авторизоваться

Введение в линейную алгебру

Примеры линейных преобразований

Вопросы и ответы