Подпространства линейного пространства. Евклидово пространство. Линейные преобразования в линейном пространстве. Представление линейного преобразования матрицей. Действия над линейными преобразованиями. Примеры линейных преобразований

Действия над линейными преобразованиями

Сложение преобразований. Пусть в n -мерном пространстве R с базисом l₁, l₂, ..., l_n заданы два линейных преобразования А и В, определяемые как y = Ax и z = Bx.

Определение 28. Суммой линейных преобразований А и В называют преобразование С, обозначаемое С = А + В, если для каждого вектора x из пространства R справедливо Сх = (А + В)х = Ax + Вx. Тогда говорят, что преобразование С преобразует вектор х в вектор q равный сумме векторов у и z, т.е. q = y + z.

Из определения 28 очевидно, что матрица С, определяющая преобразование С, должна быть равна сумме матриц преобразований А и В: С = А + В.

Умножение преобразования на число. Пусть в n -мерном пространстве R с базисом l₁, l₂, ..., l_n задано линейное преобразование А, определяемом как y = Ax, и некоторое число .

Определение 29. Произведением линейного преобразования А и числа называют преобразование С, обозначаемое 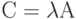, если для каждого вектора x из пространства R справедливо . Тогда говорят, что преобразование С преобразует вектор х в вектор q, равный 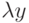, где у = Ax.

Произведение преобразований. Пусть в n -мерном пространстве R с базисом l₁, l₂, ..., l_n заданы два линейных преобразования А и В, определяемых как y = Ax и z = Bу, т.е. вектор x преобразуется преобразованием А в вектор y, который в свою очередь преобразуется в вектор z преобразованием В.

Определение 30. Произведением преобразований А и В называют преобразование С, обозначаемое С = ВА, если для каждого вектора справедливо Сх = (ВА)х = В(Ax) = Ву = z.

Заметим, что в этом случае матрица преобразования С, определяющая произведение преобразований А и В, будет выражаться произведением матриц соответствующих преобразований: С = ВА.

Обратное преобразование. Пусть в n -мерном пространстве R с базисом l₁, l₂, ..., l_n задано линейное преобразование А выражением y = Ax, где A - невырожденная квадратная матрица, для которой определена обратную матрицу A^-1 как A^-1A = AA^-1 = Е, где Е - единичная матрица^{2Единичная матрица - это диагональная матрица, все элементы которой равны единице, или единичная матрица - это квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю.}.

Определение 31. Обратным преобразованием х = A^-1у назовем такое, которое будет обратно прямому преобразованию y = Ax, причем произведение прямого и обратного преобразования будет переводить вектор в самого себя, т.е. х = A^-1у = A^-1Ax = Еx = х.

Очевидно, что матрица A^-1 обратного преобразования А^-1 будет являться обратной по отношению к матрице прямого преобразования А.