Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.10.2007 | Доступ: свободный | Студентов: 4541 / 789 | Оценка: 4.09 / 3.28 | Длительность: 11:25:00

Тема: Математика

Специальности: Математик

Теги: линейные пространства, метод Гауса, определители, векторы, матрицы

|

Вам нравится? Нравится 45 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Лекция 10:

Подпространства линейного пространства. Евклидово пространство. Линейные преобразования в линейном пространстве. Представление линейного преобразования матрицей. Действия над линейными преобразованиями. Примеры линейных преобразований

A

|

версия для печати

Таблица коэффициентов системы (9.1)

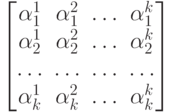
$\begin{bmatrix} \alpha_1^1 & \alpha_1^2 & \ldots & \alpha_1^k \\ \alpha_2^1 & \alpha_2^2 & \ldots & \alpha_2^k \\ \ldots & \ldots & \ldots & \ldots \\ \alpha_k^1 & \alpha_k^2 & \ldots & \alpha_k^k \end{bmatrix}$

определяет матрицу преобразования одной системы координат в другую. Заметим, так как старые единичные векторы линейно независимы, т.е. 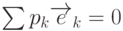$\sum p_k \overrightarrow{e}_k=0$ , только тогда, когда 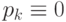$p_{k} \equiv 0$ , и определитель системы (9.1) отличен от нуля

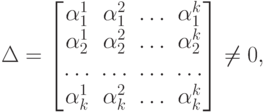
$\Delta= \begin{bmatrix} \alpha_1^1 & \alpha_1^2 & \ldots & \alpha_1^k \\ \alpha_2^1 & \alpha_2^2 & \ldots & \alpha_2^k \\ \ldots & \ldots & \ldots & \ldots \\ \alpha_k^1 & \alpha_k^2 & \ldots & \alpha_k^k \end{bmatrix} \ne 0,$

то новые векторы тоже будут линейно независимыми.

Систему (9.1) можно записать в свернутом виде:

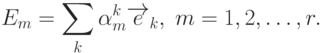$E_m=\sum_k \alpha_m^k\overrightarrow{e}_k,\; m=1,2,\ldots,r.$

( 9.2)

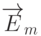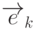Система (9.2), как и система (9.1), дает новые единичные векторы $\overrightarrow{E}_m$ как функции старых единичных векторов $\overrightarrow{e}_k$ .

Имеет место и обратный случай: возможно восстановление старых единичных векторов по известным новым. Эта задача математически сводится к решению системы (9.1) относительно 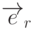$\overrightarrow{e}_r$ . В результате имеем

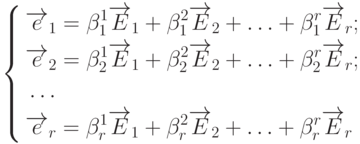$\left\{ \begin{aligned} & \overrightarrow{e}_1=\beta_1^1\overrightarrow{E}_1+\beta_1^2\overrightarrow{E}_2+\ldots+\beta_1^r\overrightarrow{E}_r; \\ & \overrightarrow{e}_2=\beta_2^1\overrightarrow{E}_1+\beta_2^2\overrightarrow{E}_2+\ldots+\beta_2^r\overrightarrow{E}_r; \\ & \ldots \\ & \overrightarrow{e}_r=\beta_r^1\overrightarrow{E}_1+\beta_r^2\overrightarrow{E}_2+\ldots+\beta_r^r\overrightarrow{E}_r \end{aligned} \right.$

( 9.3)

или в свернутом виде

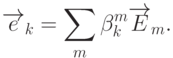$\overrightarrow{e}_k=\sum_m \beta_k^m \overrightarrow{E}_m .$

( 9.4)

Матрица $\beta$ линейного преобразования (9.4), очевидно, будет обратной матрице $\alpha$ - прямого преобразования (9.2), и, следовательно, общий элемент матрицы $\beta$ можно записать как

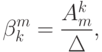
$\beta_k^m=\frac{A_m^k}{\Delta},$

где

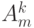- алгебраическое дополнение элемента 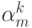$\alpha_m^k$ определителя $\Delta$ матрицы $\alpha$ .

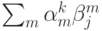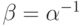Рассмотрим сумму произведений $\sum_m \alpha_m^k\beta_j^m$ . При k = j она равна единице, а при $k \ne j$ должна быть тождественно равна нулю. Это вытекает из того, что $\beta = \alpha ^{-1}$ , а произведение таких матриц есть единичная матрица, у которой элементы находятся на главной диагонали, равны 1, а все остальные - нулю.

Пользуясь символом Кронекера^{1По определению 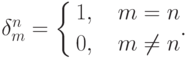.}, определим сумму произведений

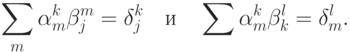
$\sum_m \alpha_m^k\beta_j^m=\delta_j^k\quad\text{и}\quad\sum\alpha_m^k\beta_k^l=\delta_m^l.$

И наконец, общий элемент матрицы $\alpha$ можно записать как

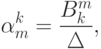
$\alpha_m^k=\frac{B_k^m}{\Delta},$

где

- алгебраическое дополнение элемента $\beta_k^m$ определителя $\Delta$ матрицы $\beta$ .

Определение 16. Говорят, что в линейном пространстве R задано скалярное произведение, если каждой паре векторов х и у из R поставлено в соответствие такое число (х,у), что выполняются следующие условия:

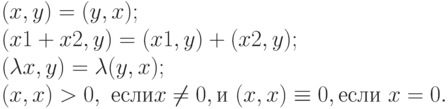
$(x,y)=(y,x); \\ (x1+x2,y)=(x1,y)+(x2,y); \\ (\lambda x,y)=\lambda (y,x); \\ (x,x)>0, \ если x\ne 0, и \ (x,x)\equiv 0, если \ x=0.$

Определение 17. Линейное пространство, в котором задано скалярное произведение, называется евклидовым пространством и обозначается Е.

Определение 18. Длиной или модулем вектора х в евклидовом пространстве называют корень квадратный из его скалярного квадрата и обозначают 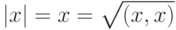$|x|=x=\sqrt{(x,x)}$ .

Из определения 18 вытекают два свойства модуля:

|x|>0 при 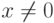$x\ne 0$ и |x|=0 при x=0 ;
$|\lambda x|=|\lambda ||x|$ .

Определение 19. Вектор х, длина которого равна 1, называют нормированным вектором.

Из определения 19 следует интересный вывод: всякий ненулевой вектор можно нормировать, т.е. умножить вектор на число 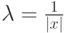$\lambda=\frac{1}{|x|}$ . Полученный вектор $y=\frac{x}{|x|}$ будет нормированным.

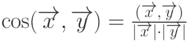Определение 20. Угол $\phi$ между векторами х и у определяется равенством $\cos(\overrightarrow{x},\overrightarrow{y})=\frac{(\overrightarrow{x},\overrightarrow{y})}{|\overrightarrow{x}|\cdot|\overrightarrow{y}|}$ .

Из определения 20 следует математическое выражение для скалярного произведения

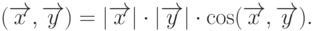$(\overrightarrow{x},\overrightarrow{y})=|\overrightarrow{x}|\cdot|\overrightarrow{y}|\cdot\cos(\overrightarrow{x},\overrightarrow{y}).$

( 9.5)

Определение 21. Два вектора евклидова пространства называют ортогональными, если их скалярное произведение равно нулю, т.е. 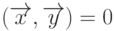$(\overrightarrow{x},\overrightarrow{y})=0$ .

Это определение следует из анализа формулы (9.5). Действительно, если длины векторов x и y не равны нулю, то только cos(x^y) может дать нуль в произведении, а это значит, что угол между векторами должен быть равен 90 $\deg$ .

Определение 22. Базис е₁, е₂, ..., е_r евклидова пространства называется ортогональным, если векторы попарно ортогональны.

Определение 23. Если базис евклидова пространства е₁, е₂, ..., е_r ортогонален и модули |е_i|=1 при i = 1, 2, ..., n, то базис называют ортонормированным.

Выразим скалярное произведение через координаты перемножаемых векторов. Пусть теперь е₁, е₂, ..., е_r - произвольный базис евклидова пространства R, в котором заданы два вектора х и y. Распишем векторы в координатной форме по заданному базису

x=x₁e₁+x₂e₂+...+x_ne_n; y=y₁e₁+y₂e₂+...+y_ne_n

и найдем скалярное произведение этих векторов. В результате имеем

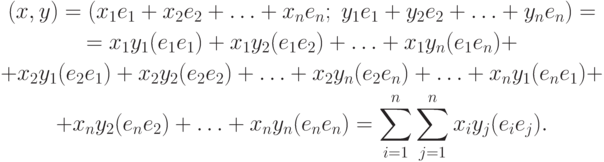
$\begin{gathered} (x,y)=(x_1 e_1+x_2 e_2+\ldots+x_n e_n;\; y_1 e_1+y_2 e_2+\ldots+y_n e_n)= \\ =x_1 y_1(e_1 e_1)+x_1 y_2(e_1 e_2)+\ldots+x_1 y_n(e_1 e_n)+ \\ +x_2 y_1(e_2 e_1)+x_2 y_2(e_2 e_2)+\ldots+x_2 y_n(e_2 e_n)+\ldots+x_n y_1(e_n e_1)+ \\ +x_n y_2(e_n e_2)+\ldots+x_n y_n(e_n e_n)=\sum_{i=1}^n\sum_{j=1}^n x_i y_j(e_i e_j). \end{gathered}$

Если базис е₁, е₂, ..., е_r ортонормирован, то в силу определения (19) скалярного произведения все произведения (е_i, e_j) будут равны нулю при 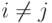$i \ne j$ и единице, при i = j. Значит,

$(x,y)=x_1 y_1+x_2 y_2+\ldots+x_n y_n .$

( 9.6)

Если х = y, то из выражения (9.6) получаем

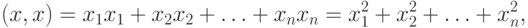
$(x,x)=x_1 x_1+x_2 x_2+\ldots+x_n x_n=x_1^2+x_2^2+\ldots+x_n^2,$

откуда можно выразить модуль (длину) вектора в ортонормированном базисе

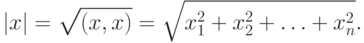$|x|=\sqrt{(x,x)}=\sqrt{x_1^2+x_2^2+\ldots+x_n^2}.$

( 9.7)

Выражение (9.7) часто называют нормой вектора х = (х₁, х₂, ..., х_n). Возвращаясь к определению (26), найдем выражение $\lambda$ как

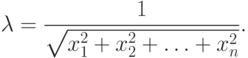$\lambda=\frac{1}{\sqrt{x_1^2+x_2^2+\ldots+x_n^2}}.$

( 9.8)

Теорема. Попарно ортогональные и отличные от нуля векторы линейно независимы.

Доказательство. Пусть х₁, х₂, ..., х_n - ненулевые векторы, попарно ортогональные, т.е. (x_i, x_j) = 0, если 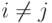$i \ne j$ . Предположим, что векторы х₁, х₂, ..., х_n линейно зависимые, т.е. существуют такие $\alpha _{1}, \alpha _{2}, \dots , \alpha _{n}$ , не равные нулю, при которых

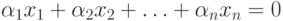$\alpha_1 x_1+\alpha_2 x_2+\ldots+\alpha_n x_n=0$

( 9.9)

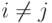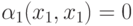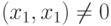Для определенности (без ограничения общности) положим $\alpha _{1} \ne 0$ . Умножим равенство (9.9) скалярно на вектор х₁, и с учетом того, что все произведения (х_i, х_j) будут равны нулю при $i \ne j$ , останется только одно произведение $\alpha _{1}(x_{1}, x_{1}) = 0$ , но $(x_{1}, x_{1}) \ne 0$ , следовательно 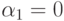$\alpha _{1} = 0$ , что противоречит нашему предположению. Значит, предположение неверно и теорема доказана.

Дальше >>

Введение в линейную алгебру

Вопросы и ответы

Авторизоваться

Введение в линейную алгебру

Вопросы и ответы