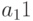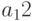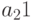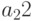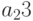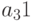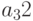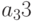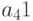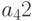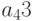НОУ ИНТУИТ | Введение в Octave. Лекция 10: Решение оптимизационных задач

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

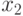Пример 10.4. План производства изделий трёх типов составляет 120 деталей ( x_1 — количество изделий первого вида, x_2 — количество изделий второго вида, 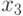x_3 — количество изделий третьего вида). Изделия можно изготовить тремя способами. При первом технологическом способе производят изделия первого типа и затраты составляют 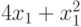$4x_{1}+x_{1}^{2}$ . Второй технологический способ предназначен для производства изделий второго типа и затраты составляют 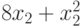$8x_{2}+x_{2}^{2}$ . Третий способ позволяет производить изделия третьего типа и затраты в нём можно рассчитать по формуле 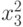$x_{3}^{2}$ . Определить, сколько изделий каждого типа надо изготовить, чтобы затраты были минимальными [1].

Сформулируем эту задачу, как задачу оптимизации. Найти минимум функции 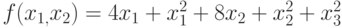$f(x_{1,}x_{2})=4x_{1}+x_{1}^{2}+8x_{2}+x_{2}^{2}+x_{3}^{2}$ при следующих ограничениях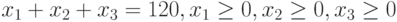 $x_{1}+x_{2}+x_{3}=120,x_{1}\ge 0,x_{2}\ge 0,x_{3}\ge 0$

	
% Оптимизируемая функция f
function y=f(x)
	y=4-x(1)+x(1)*x(1)+8*x(2)+x(2)*x(2)+x(3)*x(3);
endfunction
% Функция ограничения g(x) = 0
function z=g(x)
	z=x(1)+x(2)+x(3)-120;
endfunction
% Функция ограничения f(x) =0
function u= fi(x)
	fi =[x(1); x(2); x(3)];
endfunction
x0 = [0; 0; 0]; [x, obj, info, iter]= sqp(x0, @f, @g)
% Результаты решения
x =
	40.000
	38.000
	42.000
obj = 5272.0
info = 101
iter = 8

Листинг 10.6. Решение задачи оптимизации из примера 10.4

Минимальные затраты составят 5272 денежных единицы, при этом будет произведено 40 изделий первого вида, 38 — второго и 42 — третьего. Для решения задачи было проведено 8 итераций.

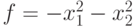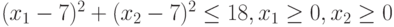Пример 10.5. Найти максимум функции $f=-x_{1}^{2}-x_{2}^{2}$ при ограничениях $(x_{1}-7)^{2}+(x_{2}-7)^{2}\le 18, x_{1}\ge 0, x_{2}\ge 0$ .

В этой задаче необходимо свести задачу на максимум к задаче на минимум, а также путём умножения на -1 заменить знак в неравенстве. Текст программы-решения задачи в Octave представлен в листинге 10.7. Функция достигает своего максимального значения -32 в точке (4, 4).

	
function y=f(x)
	y=-x(1)*x(1)*x(2)*x(2);
endfunction
function y=f1(x)
	y= -f(-x);
endfunction
function u= fi(x)
	u=[-(x(1)-7)^2-(x(2)-7)^2+18;x(1); x(2)];
endfunction
x0 = [0; 0]; [xopt, obj, info, iter]= sqp(x0, @f1, [ ], @fi)
f(xopt)
% Результаты решения
xopt =
	4.0000
	4.0000
obj =32.000
info =101
iter =8
ans =-32.000

Листинг 10.7. Решение задачи из примера 10.5

Следующим классом оптимизационных задач, рассматриваемых в этой главе, будут задачи линейного программирования (ЗЛП).