Решение оптимизационных задач

10.2.2 Решение задач линейного программирования в Octave

Для решения задач линейного программирования в Octave существует функция

Здесь:

• — вектор-столбец, включающий в себя коэффициенты при неизвестных функции цели, размерность вектора c равна количеству неизвестных в задаче линейного программирования;
• — матрица при неизвестных из левой части системы ограничений, количество строк матрицы равно количеству ограничений , а количество столбцов совпадает с количеством неизвестных ;
• — вектор-столбец содержит свободные члены системы ограничений, размерность вектора равна количеству ограничений .
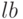• — вектор-столбец размерности , содержащий верхнюю систему ограничений 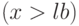, по умолчанию 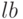— вектор столбец, состоящий из нулей;
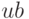• — вектор-столбец размерности , содержащий нижнюю систему ограничений 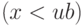, по умолчанию верхняя система ограничений отсутствует, подразумевается, что все значения вектора 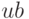равны +\infty;
• — массив символов размерности , определяющий тип ограничения (например, (10.7) или (10.8)), элементы этого век-тора могут принимать одно из следующих значений:
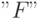• — ограничение будет проигнорировано,
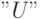• — ограничение с верхней границей ,
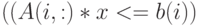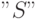• — ограничение в виде равенства ,
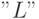• — ограничение с верхней границей ,
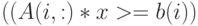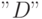• — двойное ограничение 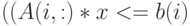и ;
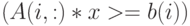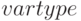• — массив символов размерности , который определяет тип переменной 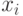"C" — вещественная переменная, "I" —целочисленная переменная;
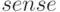• — значение, определяющее тип задачи оптимизации:
• 1 — задача минимизации,
• -1 — задача максимизации;
• — структура, определяющая параметры оптимизационных алгоритмов, при обращении к функции glpk.

Во многих случаях достаточно значений структуры param по умолчанию, в этом случае последний параметр в функции 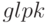можно не указывать. Подробное описание структуры выходит за рамки книги, в случае необходимости его использования авторы рекомендуют обратиться ко встроенной справке Octave.

Функция 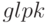возвращает следующие значения:

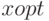• — массив значений , при котором функция цели принимает оптимальное значение;
• — оптимальное значение функции цели;
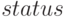• — переменная, определяющая как решена задача оптимизация, при 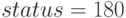, решение найдено и задача оптимизации решена полностью^{2Если 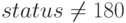, то полученному решению доверять нельзя, подробнее о значениях переменной 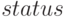в этом случае можно прочитать в справке.};
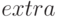• — структура, включающая следующие поля:
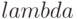• — множители Лагранжа;
• — время в секундах, затраченное на решение задачи;
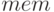• — память в байтах, которая была использована, при решении задачи (значение недоступно, если была использована библиотека линейного программирования GLPK 4.15^{3В последней на момент написания книги версии Octave использовалась библиотека GLPK версии 4.38.}и выше).

Рассмотрим несколько примеров решения задач линейного программирования.