НОУ ИНТУИТ | Введение в Octave. Лекция 8: Интегрирование и дифференцирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 12.03.2015 | Доступ: свободный | Студентов: 582 / 64 | Длительность: 20:55:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.3.3 Интегрирование по квадратурным формулам Гаусса

Запишем в общем виде квадратурную формулу для функции заданной на промежутке [-1; 1]

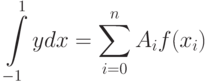
$\int\limits_{-1}^1ydx=\sum \limits_{i=0}^nA_if(x_i)$

Попытаемся найти коэффициенты 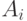A_i и узловые точки 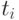t_i , таким образом, чтобы квадратурная формула была точной для всех полиномов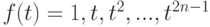 $f(t)=1,t,t^2,...,t^{2n-1}$

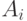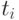В этом случае построение квадратурной формулы приводит к определению A_i и t_i из нелинейной системы 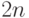уравнений:

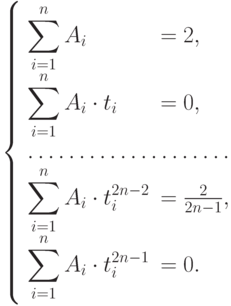
$\left\{ \begin{array}{ll} \displaystyle\sum _{i=1}^{n}A_{i}&=2,\\ \displaystyle\sum _{i=1}^{n}A_{i}\cdot t_{i}&=0,\\ \hdotsfor{2}\\ \displaystyle\sum _{i=1}^{n}A_{i}\cdot t_{i}^{2n-2}&=\frac{2}{2n-1},\\ \displaystyle\sum _{i=1}^{n}A_{i}\cdot t_{i}^{2n-1}&=0. \end{array} \right.$

Решение нелинейной системы задача не тривиальная, но её можно обойти, если знать, что значениями 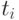t_i квадратурной формулы служат корни многочлена Лежандра

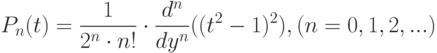
$P_n(t)=\frac{1}{2^n\cdot n!}\cdot\frac{d^n}{dy^n}((t^2-1)^2),(n=0,1,2,...)$

Как известно, корни полинома Лежандра существуют при любом , различны и принадлежат интервалу [-1; 1].

Итак, квадратурной формулой Гаусса называют выражение

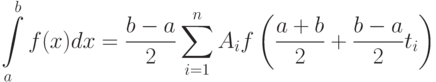
$\int\limits_{a}^bf(x)dx=\frac{b-a}{2}\sum \limits_{i=1}^nA_if \left(\frac{a+b}{2}+\frac{b-a}{2}t_i\right)$

где 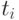t_i — корни полинома Лежандра, а 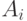A_i определяется интегрирова-нием базисных многочленов Лежандра 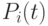P_i(t) степени n - 1 :

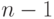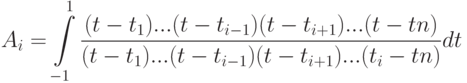
$A_i=\int\limits_{-1}^1\frac{(t-t_1)...(t-t_{i-1})(t-t_{i+1})...(t-tn)}{(t-t_1)...(t-t_{i-1})(t-t_{i+1})...(t_i-tn)}dt$

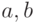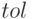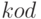В Octave интегрирование по квадратуре Гаусса выполняет функция [F, kod, K, err] = quad(name, a, b, tol, sing) , где: name — имя функции, задающей подынтегральное выражение; a, b — пределы интегрирования; tol — точность вычислений; sing — вектор значений, близких к тем, в которых подынтегральная функция терпит разрыв; — значение интеграла; kod — код ошибки в решении (0 — решение завершено успешно); — количество итераций; err — 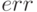погрешность вычислений.

Пример 8.14. Вычислить интеграл 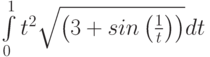$\int\limits_{0}^1t^2\sqrt{\left(3+sin \left(\frac{1}{t}\right)\right)}dt$

Обратите внимание, что в нижней границе интегрирования подынтегральная функция терпит разрыв. Решение примера с применением функции 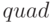quad приведено в листинге 8.16.

	
clear all;
function y=f(x)
	y=(x.^2).-sqrt(3+sin(1./x));
end;
>>> format long
>>> [F, kod, K, err]=quad(’f’, 0, 1)
F = 0.654343719149802
kod = 0
K = 1323
err = 1.37557012147481 e-08
>>> [F, kod, K, err]=quad(’f’, 0, 1, 1.0 e-05)
F = 0.654343738854992
kod = 0
K = 315
err = 3.82733563379833 e -06
>>> [F, kod, K, err]=quad(’f’, 0, 1, 1.0 e-20)
F = 0.654343718970708
kod = 0
K = 1491
err = 9.39557628735834 e-09
>>> [F, kod, K, err]=quad(’f’, 0, 1, 1.0 e-20,0.1)
F = 0.654343710193938
kod = 0
K = 840
err = 5.80259740257105 e-09
>>> [F, kod, K, err]=quad(’f’, 0, 1, 1.0 e- 20,0.001)
F = 0.654343718720156
kod = 0
K = 1596
err = 8.35248716562893 e-09

Листинг 8.16. Вычисление интеграла через quad (пример 8.14).

Функции

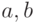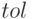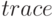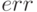F = quadl(f, a, b[, tol, trace]) и [F, err] = quadgk(f, a, b[, tol, trace]) , где: name — имя функции, задающей подынтегральное выражение; a, b — пределы интегрирования; tol — точность вычислений; trace — таблица промежуточных вычислений; — значение интеграла; err — погрешность вычислений; также выполняют интегрирование по квадратуре Гаусса. В этих функциях специальным образом подбирается шаг. В первом случае по методу Гаусса-Лобатто, во втором Гаусса-Конрада.

Пример 8.15. Вычислить интеграл

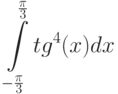
$\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}tg^4(x)dx$

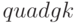Решение примера с применением функций quadl и quadgk приведено в листинге 8.17.

	
function y=f(x)
	y = tan(x).^4;
end;
>>> format long
>>> [F]= quadl (’f’,-pi/3, pi/3, 1.0 e-05)
F = 2.09439512983937
>>> [F, err]=quadgk(’f’, -pi/3, pi/3, 1.0 e-05)
F = 2.09439510239319
err = 1.02555919485880 e-12

Листинг 8.17. Вычисление интеграла через quadl и quadgk (пр. 8.15).

Дальше >>

Авторизоваться

Введение в Octave

Интегрирование и дифференцирование

8.3.3 Интегрирование по квадратурным формулам Гаусса

Вопросы и ответы