|
Возможна ли разработка приложения на Octave с GUI? |
Интегрирование и дифференцирование
8.3 Численное интегрирование
Пусть дана функция 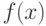 , известно, что она непрерывна на интервале
, известно, что она непрерывна на интервале ![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) и уже определена её первообразная
и уже определена её первообразная  , тогда определённый интеграл от этой функции можно вычислить в пределах от
, тогда определённый интеграл от этой функции можно вычислить в пределах от
 до
до  по формуле Ньютона–Лейбница:
по формуле Ньютона–Лейбница:
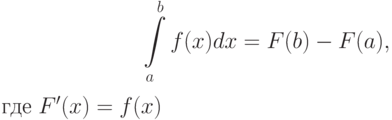
Пример 8.9. Вычислить определённый интеграл
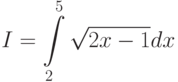
К сожалению в Octave не предусмотрены средства символьного интегрирования, поэтому обратимся к таблице интегралов и найдём, что
![I=\int\sqrt{2x-1}dx=\frac{1}{3}\sqrt[3]{(2x-1)^2}+C](/sites/default/files/tex_cache/77d154ab379ff639cf7775e89424198a.png)
Теперь вычислим интеграл по формуле Ньютона–Лейбница:
clear all; % Функция, определяющая подынтегральное выражение % x — переменная интегрирования, C — постоянная интегрирования. function y=F(x,C) y=1/3-(2-x-1)^(3/2)+C; end; >>> a =2; b=5; % Вычисление интеграла по формуле Ньютона-Лейбница >>> I = F(b, 0)-F(a, 0) I = 7.2679Листинг 8.10. Вычисление определённого интеграла (пример 8.9).
На практике часто встречаются интегралы с первообразной, которая не может быть выражена через элементарные функции или является слишком сложной, что затрудняет, или делает невозможным, вычисления по формуле Ньютон-Лейбница. Кроме того, нередко подынтегральная функция задаётся таблицей или графиком и тогда понятие первообразной вообще теряет смысл. В этом случае большое значение имеют численные методы интегрирования, основная задача которых заключается в вычислении значения определённого интеграла на основании значений подынтегральной функции.
Численное вычисление определённого интеграла называют механической квадратурой. Формулы, соответствующие тому или иному численному методу приближённого интегрирования, называют квадратурными. Подобное название связано с геометрическим смыслом определённого интеграла: значение определённого интеграла
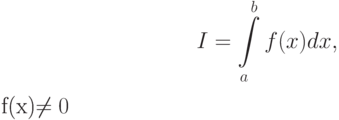
равно площади криволинейной трапеции с основаниями ![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) и
и 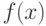 .
.
Вообще говоря, классические учебники по численной математике предлагают немало методов интегрирования, но здесь мы рассмотрим только те методы, которые имеют непосредственное отношение к функциям Octave.
8.3.1 Интегрирование по методу трапеций
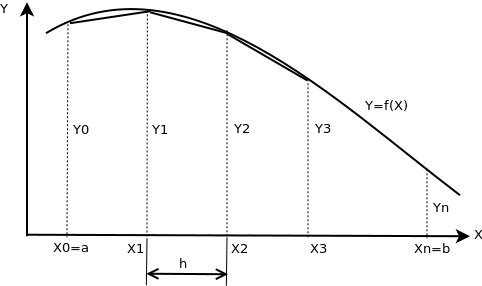
Изложим геометрическую интерпретацию интегрирования по методу трапеций. Для этого участок интегрирования ![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) разобьём точками на n равных частей (рис. 8.5), причём
разобьём точками на n равных частей (рис. 8.5), причём 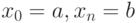
Тогда длина каждой части будет равна 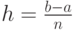 , а значение абсциссы каждой из точек разбиения можно вычислить по формуле
, а значение абсциссы каждой из точек разбиения можно вычислить по формуле  . Теперь из каждой точки
. Теперь из каждой точки 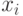 проведём перпендикуляр до пересечения с кривой
проведём перпендикуляр до пересечения с кривой 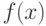 , а затем заменим каждую из полученных криволинейных трапеций прямолинейной. Приближённое значение интеграла будем рассматривать как сумму площадей прямолинейных трапеций, причём площадь отдельной трапеции составляет
, а затем заменим каждую из полученных криволинейных трапеций прямолинейной. Приближённое значение интеграла будем рассматривать как сумму площадей прямолинейных трапеций, причём площадь отдельной трапеции составляет  , следовательно, площадь искомой фигуры вычисляют по формуле:
, следовательно, площадь искомой фигуры вычисляют по формуле:
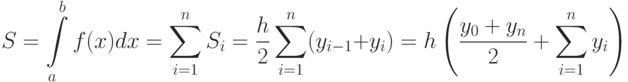
Таким образом, получена квадратурная формула трапеций для численного интегрирования:
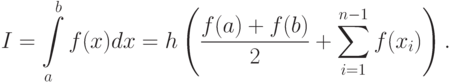
Функции 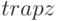 и
и  реализуют численное интегрирование по методу трапеций в Octave.
реализуют численное интегрирование по методу трапеций в Octave.
Площадь фигуры под графиком функции 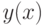 , в котором все точки заданы векторами
, в котором все точки заданы векторами  и
и  , вычисляет команда
, вычисляет команда 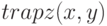 .
.
| x | -1.5708 | -1.0708 | -0.5708 | -0.0708 | 0.4292 | 0.9292 | 1,4292 |
| y | 0 | 0.47943 | 0.84147 | 0.99749 | 0.90930 | 0.59847 | 0.14112 |
Если вызвать функцию 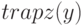 с одним аргументом, то будет вычислена площадь фигуры под графиком функции
с одним аргументом, то будет вычислена площадь фигуры под графиком функции 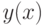 , в котором все точки заданы векторами
, в котором все точки заданы векторами  и
и  , причём по умолчанию элементы вектора
, причём по умолчанию элементы вектора  принимают значения номеров элементов вектора
принимают значения номеров элементов вектора  .
.
Пример 8.10. Вычислить интеграл от функции y(x) = cos(x). Значения функции представлены в табл. 8.1.
Решение примера представлено в листинге 8.11.
>>> clear all; >>> x=[-1.5708 -1.0708 -0.5708 -0.0708 0.4292 0.9292 1.4292]; >>> y=[0 0.47943 0.84147 0.99749 0.90930 0.59847 0.14112]; >>> I=trapz(x, y) I = 1.9484Листинг 8.11. Вычисление интеграла методом трапеций (пример 8.10).
Пример 8.11. Вычислить интеграл 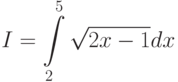
Листинг 8.12 содержит несколько вариантов решения данного примера. В первом случае интервал интегрирования делится на отрезки с шагом 1, во втором 0.5, в третьем 0.1 и в четвёртом 0.05. Не трудно заметить, что чем больше точек разбиения, тем точнее значение искомого интеграла. Решение можно сравнить с результатом полученным в задаче 8.9, где этот же интеграл был найден по формулам Ньютона-Лейбница (листинг 8.10).
clear all; % Вариант 1. h=1 >>> x = 2:5; y=sqrt(2-x-1); I1=trapz(x, y) % Вариант 2. h=0.5 >>> x = 2:0.5:5; y=sqrt(2-x-1); I2=trapz(x, y) % Вариант 3. h=0.1 >>> x = 2:0.1:5; y=sqrt(2-x-1); I3=trapz(x, y) % Вариант 4. h=0.05 >>> x = 2:0.05:5; y=sqrt(2-x-1); I4=trapz(x, y) % Результаты интегрирования I1 = 7.2478 I2 = 7.2629 I3 = 7.2677 I4 = 7.2679Листинг 8.12. Вычисление интеграла с разной точностью (пр. 8.11).
В листинге 8.13 приведён пример использования функции 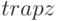 с одним аргументом. Как видим, в первом случае значение интеграла, вычисленного при помощи этой функции, не точно и совпадает со значением, полученным функцией
с одним аргументом. Как видим, в первом случае значение интеграла, вычисленного при помощи этой функции, не точно и совпадает со значением, полученным функцией 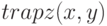 на интервале [2, 5] с шагом 1 (листинг 8.12, первый вариант). То есть мы нашли сумму площадей трёх прямолинейных трапеций с основанием
на интервале [2, 5] с шагом 1 (листинг 8.12, первый вариант). То есть мы нашли сумму площадей трёх прямолинейных трапеций с основанием  и боковыми сторонами, заданными вектором y. Во втором случае, при попытке увеличить точность интегрирования, значение интеграла существенно увеличивается. Дело в том что, уменьшив шаг разбиения интервала интегрирования до 0.05, мы увеличили количество элементов векторов
и боковыми сторонами, заданными вектором y. Во втором случае, при попытке увеличить точность интегрирования, значение интеграла существенно увеличивается. Дело в том что, уменьшив шаг разбиения интервала интегрирования до 0.05, мы увеличили количество элементов векторов  и
и  и применение функции
и применение функции 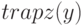 приведёт к вычислению суммы площадей шестидесяти трапеций с основанием
приведёт к вычислению суммы площадей шестидесяти трапеций с основанием  и боковыми сторонами, заданными вектором
и боковыми сторонами, заданными вектором  . Таким образом, в первом и втором примерах листинга 8.13 вычисляются площади совершенно разных фигур.
. Таким образом, в первом и втором примерах листинга 8.13 вычисляются площади совершенно разных фигур.
% Пример 1. >>> x = 2:5; y=sqrt(2-x-1); I=trapz(y) I = 7.2478 % Пример 2. >>> x = 2:0.05:5; y=sqrt(2-x-1); I=trapz(y) I = 145.36Листинг 8.13. Особенности вычисления интеграла через trapz (y).
Функция  выполняет так называемое "интегрирование с накоплением" по методу трапеций. Это означает, что она, так же как и
выполняет так называемое "интегрирование с накоплением" по методу трапеций. Это означает, что она, так же как и 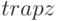 , вычисляет площадь фигуры под графиком функции
, вычисляет площадь фигуры под графиком функции 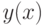 , но результатом её работы является вектор, состоящий из промежуточных вычислений. То есть, если общая площадь
, но результатом её работы является вектор, состоящий из промежуточных вычислений. То есть, если общая площадь  криволинейной трапеции сформирована из суммы площадей
криволинейной трапеции сформирована из суммы площадей
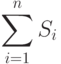
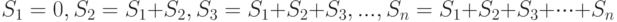
Таким образом, последний элемент вектора будет равен искомой площади фигуры  . Функцию интегрирования с накоплением можно вызывать в форматах
. Функцию интегрирования с накоплением можно вызывать в форматах 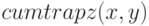 и
и 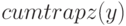 , где
, где  и
и  векторы, определяющие функцию
векторы, определяющие функцию 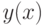 .
.
Пример 8.12. Вычислить интеграл 
Листинг 8.14 демонстрирует применение функции интегрирования с накоплением  к поставленной задаче. Там же приведена интерпретация работы этой функции с помощью команды
к поставленной задаче. Там же приведена интерпретация работы этой функции с помощью команды 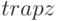 .
.
>>> x = 0:0.1:pi/2; y=(5+sin(x)).^(-1); % 1. Интегрирование с накоплением >>> I1=cumtrapz(x, y) I1 = Columns 1 through 8: 0.0 0.0198 0.03923 0.05829 0.07701 0.09541 0.11352 0.13136 Columns 9 through 16: 0.1489 0.1663 0.18356 0.2006 0.2175 0.23434 0.25108 0.2677 % 2. Обычное интегрирование >>> I2=trapz(x, y) % Значение I2 совпадает с последним значением вектора I1 I2 = 0.26777 % 3. Интегрирование на левой части интервала от 0 до 1 >>> x = 0:0.1:1; y=(5+sin(x)).^(-1); >>> I3=trapz(x, y) % Значение I3 совпадает с 11-м значением вектора I1 I3 = 0.18356Листинг 8.14. Вычисление интеграла через cumtrapz (пример 8.12).