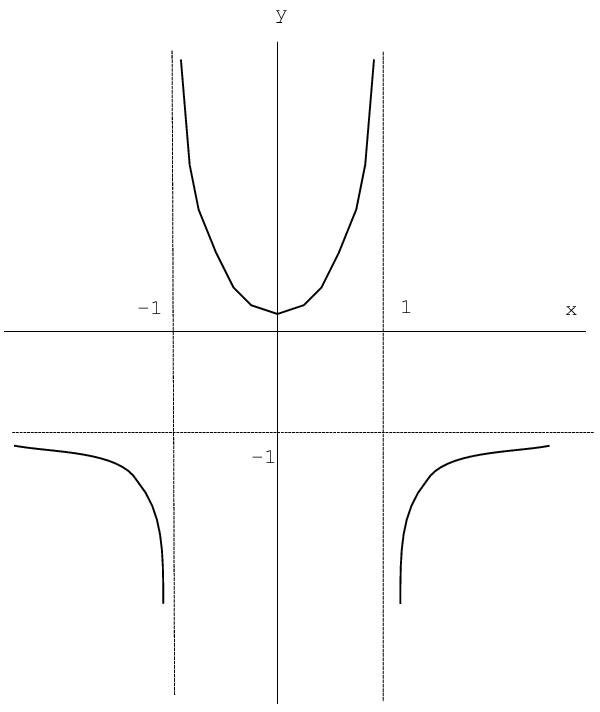Задачи высшей математики с Maxima
3.4.2 Выпуклость функции
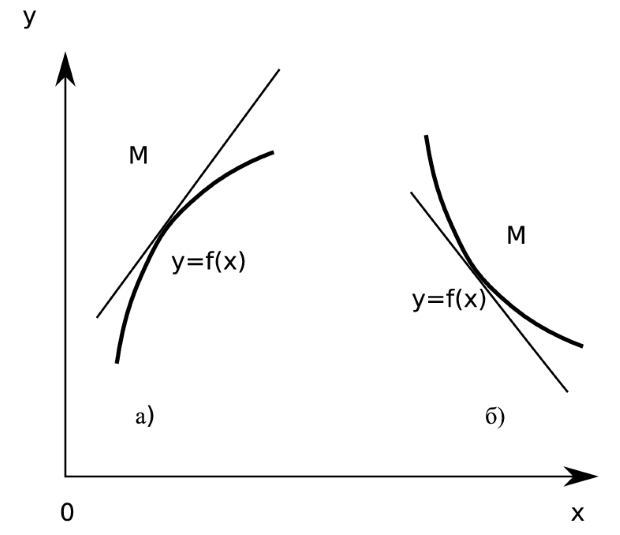
Определение. График функции 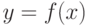 называется выпуклым в интервале
называется выпуклым в интервале 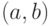 , если он расположен ниже касательной, проведенной в любой точке этого интервала (см. рис. 3.8а).
, если он расположен ниже касательной, проведенной в любой точке этого интервала (см. рис. 3.8а).
График функции  называется вогнутым в интервале
называется вогнутым в интервале 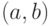 , если он расположен выше касательной, проведенной в любой точке этого интервала (см. рис. 3.8б).
, если он расположен выше касательной, проведенной в любой точке этого интервала (см. рис. 3.8б).
3.4.2.1 Необходимые и достаточные условия выпуклости (вогнутости) функции
Для определения выпуклости (вогнутости) функции на некотором интервале можно использовать следующие теоремы.
Теорема 1. Пусть функция  определена и непрерывна на интервале
определена и непрерывна на интервале  и имеет конечную производную
и имеет конечную производную 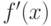 . Для того, чтобы функция
. Для того, чтобы функция  была выпуклой (вогнутой) в
была выпуклой (вогнутой) в  , необходимо и достаточно, чтобы ее производная
, необходимо и достаточно, чтобы ее производная 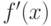 убывала (возрастала) на этом интервале.
убывала (возрастала) на этом интервале.
Теорема 2. Пусть функция  определена и непрерывна вместе со своей производной
определена и непрерывна вместе со своей производной 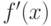 на
на  и имеет внутри
и имеет внутри  непрерывную вторую производную
непрерывную вторую производную 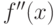 . Для выпуклости (вогнутости) функции
. Для выпуклости (вогнутости) функции
 в
в  необходимо и достаточно, чтобы внутри
необходимо и достаточно, чтобы внутри 

Докажем теорему 2 для случая выпуклости функции  .
.
Необходимость. Возьмем произвольную точку  . Разложим функцию
. Разложим функцию  около точки
около точки  в ряд Тейлора
в ряд Тейлора

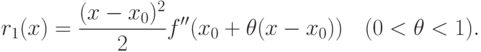
Уравнение касательной к кривой  в точке, имеющей абсциссу
в точке, имеющей абсциссу  :
:
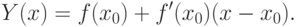
Тогда превышение кривой  над касательной к ней в точке
над касательной к ней в точке  равно
равно
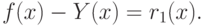
Таким образом, остаток 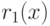 равен величине превышения кривой
равен величине превышения кривой  над касательной к ней в точке
над касательной к ней в точке  . В силу непрерывности
. В силу непрерывности 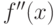 , если
, если 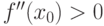 , то и
, то и 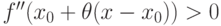 для
для  , принадлежащих достаточно малой окрестности точки
, принадлежащих достаточно малой окрестности точки  , а потому, очевидно, и
, а потому, очевидно, и 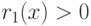 для любого отличного от
для любого отличного от  значения
значения  , принадлежащего к указанной окрестности.
, принадлежащего к указанной окрестности.
Значит, график функции  лежит выше касательной
лежит выше касательной  и кривая
и кривая  выпукла в произвольной точке
выпукла в произвольной точке  .
.
Достаточность. Пусть кривая  выпукла на промежутке
выпукла на промежутке  . Возьмем произвольную точку
. Возьмем произвольную точку  .
.
Аналогично предыдущему разложим функцию  около точки
около точки
 в ряд Тейлора
в ряд Тейлора

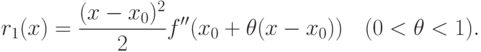
Превышение кривой  над касательной к ней в точке, имеющей абсциссу
над касательной к ней в точке, имеющей абсциссу  , определяемой выражением
, определяемой выражением  равно
равно
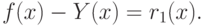
Так как превышение положительно для достаточно малой окрестности точки  , то положительна и вторая производная
, то положительна и вторая производная  . При стремлении
. При стремлении 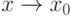 получаем, что для произвольной точки
получаем, что для произвольной точки 
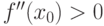 .
.
Пример. Исследовать на выпуклость (вогнутость) функцию 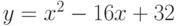 .
.
Ее производная 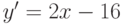 возрастает на всей числовой оси, значит по теореме 1 функция вогнута на
возрастает на всей числовой оси, значит по теореме 1 функция вогнута на 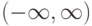 .
.
Ее вторая производная 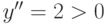 , поэтому по теореме 2 функция вогнута на
, поэтому по теореме 2 функция вогнута на 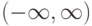 .
.
3.4.2.2 Точки перегиба
Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла и вогнута.
Из этого определения следует, что точки перегиба — это точки точки экстремума первой производной. Отсюда вытекают следующие утверждения для необходимого и достаточного условий перегиба.
Теорема (необходимое условие перегиба). Для того чтобы точка  являлась точкой перегиба дважды дифференцируемой функции
являлась точкой перегиба дважды дифференцируемой функции 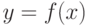 , необходимо, чтобы ее вторая производная в этой точке равнялась нулю (
, необходимо, чтобы ее вторая производная в этой точке равнялась нулю (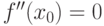 ) или не существовала.
) или не существовала.
Теорема (достаточное условие перегиба). Если вторая производная 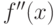 дважды дифференцируемой функции
дважды дифференцируемой функции 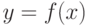 при переходе через некоторую точку
при переходе через некоторую точку  меняет знак, то
меняет знак, то  есть точка перегиба.
есть точка перегиба.
Отметим, что в самой точке вторая производная 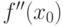 может не существовать.
может не существовать.
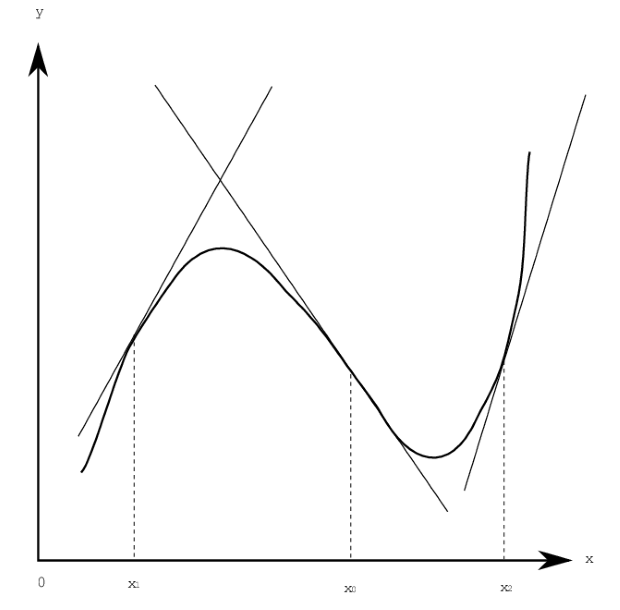
Геометрическая интерпретация точек перегиба иллюстрируется рис. 3.9
В окрестности точки  функция выпукла и график ее лежит ниже касательной, проведенной в этой точке. В окрестности точки
функция выпукла и график ее лежит ниже касательной, проведенной в этой точке. В окрестности точки 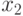 функция вогнута и график ее лежит выше касательной, проведенной в этой точке. В точке перегиба
функция вогнута и график ее лежит выше касательной, проведенной в этой точке. В точке перегиба  касательная разделяет график функции на области выпуклости и вогнутости.
касательная разделяет график функции на области выпуклости и вогнутости.
3.4.2.3 Исследование функции на выпуклость и наличие точек перегиба
1. Найти вторую производную 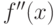 .
.
2. Найти точки, в которых вторая производная 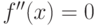 или не существует.
или не существует.
3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости или вогнутости и наличии точек перегиба.
Пример. Исследовать функцию 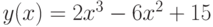 на выпуклость и наличие точек перегиба.
на выпуклость и наличие точек перегиба.
1. 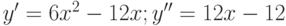 .
.
2. Вторая производная равна нулю при 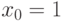 .
.
3. Вторая производная  меняет знак при
меняет знак при 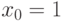 , значит точка
, значит точка 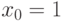 — точка перегиба.
— точка перегиба.
На интервале 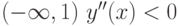 , значит функция
, значит функция 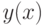 выпукла на этом интервале.
выпукла на этом интервале.
На интервале 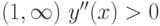 , значит функция
, значит функция 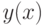 вогнута на этом интервале.
вогнута на этом интервале.
3.4.2.4 Общая схема исследования функций и построения графика
При исследовании функции и построении ее графика рекомендуется использовать следующую схему:
- Найти область определения функции.
- Исследовать функцию на четность — нечетность. Напомним, что график четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
- Найти вертикальные асимптоты.
- Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
- Найти экстремумы и интервалы монотонности функции.
- Найти интервалы выпуклости функции и точки перегиба.
- Найти точки пересечения с осями координат.
Исследование функции проводится одновременно с построением ее графика.
Пример. Исследовать функцию 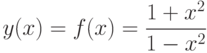 и построить ее график.
и построить ее график.
1. Область определения функции — 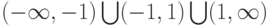 .
.
2. Исследуемая функция — четная 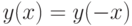 , поэтому ее график симметричен относительно оси ординат.
, поэтому ее график симметричен относительно оси ординат.
3. Знаменатель функции обращается в ноль при 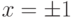 , поэтому график функции имеет вертикальные асимптоты
, поэтому график функции имеет вертикальные асимптоты 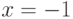 и
и 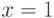 .
.
Точки 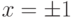 являются точками разрыва второго рода, так как пределы слева и справа в этих точках стремятся к
являются точками разрыва второго рода, так как пределы слева и справа в этих точках стремятся к 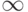 .
.
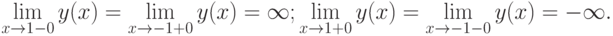
4. Поведение функции в бесконечности.
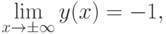
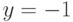 .
.5. Экстремумы и интервалы монотонности. Находим первую производную
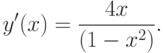
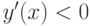 при
при 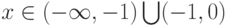 , поэтому в этих интервалах функция
, поэтому в этих интервалах функция 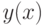 убывает.
убывает.
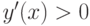 при
при 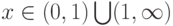 , поэтому в этих интервалах функция
, поэтому в этих интервалах функция 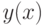 возрастает.
возрастает.
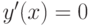 при
при 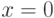 , поэтому точка
, поэтому точка  является критической точкой.
является критической точкой.
Находим вторую производную
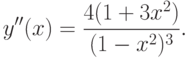
Так как 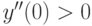 , то точка
, то точка  является точкой минимума функции
является точкой минимума функции 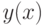 .
.
6. Интервалы выпуклости и точки перегиба.
Функция 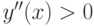 при
при  , значит на этом интервале функция
, значит на этом интервале функция 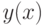 вогнута.
вогнута.
Функция  при
при  , значит на этих интервалах функция
, значит на этих интервалах функция 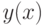 выпукла.
выпукла.
Функция  нигде не обращается в ноль, значит точек перегиба нет.
нигде не обращается в ноль, значит точек перегиба нет.
7. Точки пересечения с осями координат.
Уравнение  , имеет решение
, имеет решение 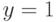 , значит точка пересечения графика функции
, значит точка пересечения графика функции 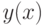 с осью ординат (0, 1).
с осью ординат (0, 1).
Уравнение 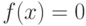 не имеет решения, значит точек пересечения с осью абсцисс нет.
не имеет решения, значит точек пересечения с осью абсцисс нет.
С учетом проведенного исследования можно строить график функции
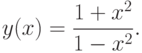
Схематически график функции 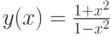 изображен на рис. 3.10.
изображен на рис. 3.10.
3.4.2.5 Асимптоты графика функции
Определение. Асимптотой графика функции y = f(x) называется прямая, обладающая тем свойством, что расстояние от точки ( ) до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат.
) до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат.
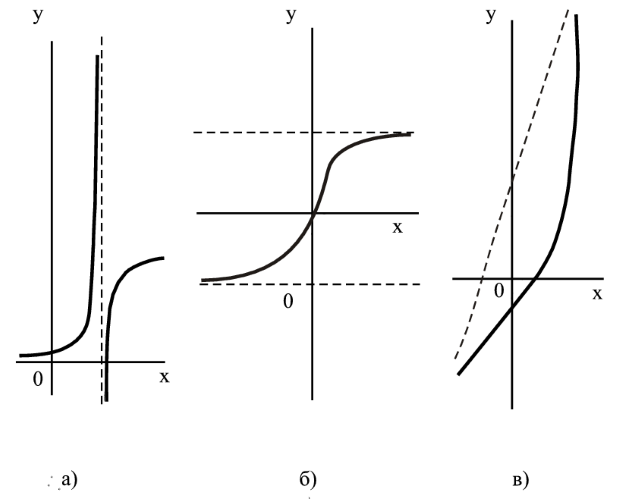
Асимптоты бывают 3 видов: вертикальные (см. рис. 3.11а), горизонтальные (см. рис. 3.11б) и наклонные (см. рис. 3.11в).
Асимптоты находят, используя следующие теоремы:
Теорема 1. Пусть функция 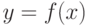 определена в некоторой окрестности точки
определена в некоторой окрестности точки  (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при
(исключая, возможно, саму эту точку) и хотя бы один из пределов функции при 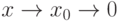 (слева) или
(слева) или 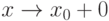 (справа) равен бесконечности. Тогда прямая является
(справа) равен бесконечности. Тогда прямая является 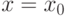 вертикальной асимптотой графика функции
вертикальной асимптотой графика функции 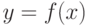 .
.
Вертикальные асимптоты 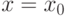 следует искать в точках разрыва функции
следует искать в точках разрыва функции 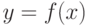 .
.
Теорема 2. Пусть функция 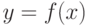 определена при достаточно больших
определена при достаточно больших  и существует конечный предел функции
и существует конечный предел функции
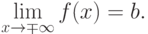
 есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции 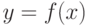 .
.Теорема 3. Пусть функция 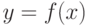 определена при достаточно больших
определена при достаточно больших  и существуют конечные пределы
и существуют конечные пределы

![\lim_{x\to\mp\infty}[f(x)-kx]=b.](/sites/default/files/tex_cache/d2fac795d21dd0f745684fb5329de2e5.png)
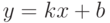 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 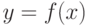 .
.Пример. Найти асимптоты графика дробно-рациональной функции
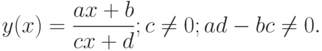
Если  , то дробно-рациональная функция становится линейной
, то дробно-рациональная функция становится линейной
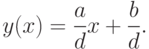
Особая точка 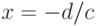 . Найдём предел
. Найдём предел 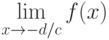 .
.
Перепишем дробно-рациональную функцию в виде:
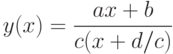
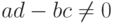 то при
то при  числитель дробно-рациональной функции не стремится к нулю. Поэтому прямая
числитель дробно-рациональной функции не стремится к нулю. Поэтому прямая  — асимптота графика дробно-рациональной функции.
— асимптота графика дробно-рациональной функции.Найдём предел  .
.

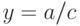 — является горизонтальной асимптотой дробно-рациональной функции.
— является горизонтальной асимптотой дробно-рациональной функции.Пример. Найти асимптоты кривой 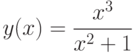 .
.
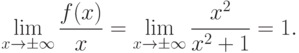
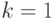 .
.Теперь ищем  .
.
![b=\lim_{x\to\pm\infty}\left[\frac{x^3}{x^2+1}-x\right]=
\lim_{x\to\pm\infty}\left(\frac{-x}{x^2+1}\right)](/sites/default/files/tex_cache/737f047c86692b5a963b81e4fea6124c.png)
Функция 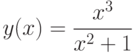 имеет наклонную асимптоту
имеет наклонную асимптоту 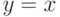 .
.
3.4.2.6 Свойства функций, непрерывных на отрезке. Теоремы Вейерштрасса
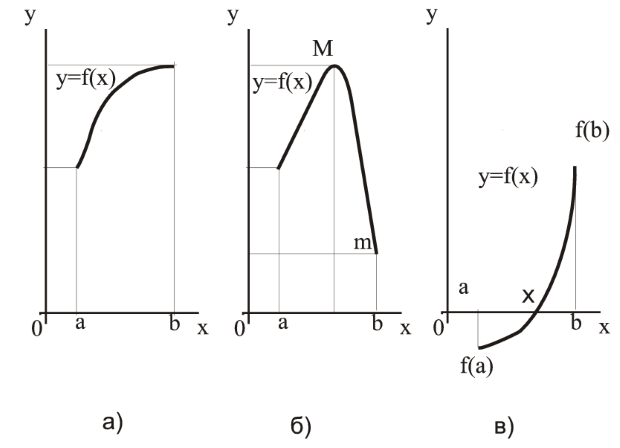
- Если функция
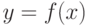 непрерывна на отрезке
непрерывна на отрезке ![[a,b]](/sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , то она ограничена на этом отрезке, т.е. существуют такие постоянные и конечные числа
, то она ограничена на этом отрезке, т.е. существуют такие постоянные и конечные числа  и
и  , что
(см. рис. 3.12а).
, что
(см. рис. 3.12а).
- Если функция
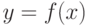 непрерывна на отрезке [
непрерывна на отрезке [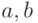 ], то она достигает на этом отрезке наибольшего значения
], то она достигает на этом отрезке наибольшего значения  и наименьшего значения m (см. рис. 3.12б).
и наименьшего значения m (см. рис. 3.12б). - Если функция
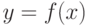 непрерывна на отрезке [
непрерывна на отрезке [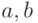 ], и значения её на концах отрезка
], и значения её на концах отрезка 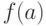 и
и 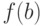 имеют противоположные знаки, то внутри отрезка найдётся точка
имеют противоположные знаки, то внутри отрезка найдётся точка 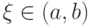 , такая, что
, такая, что 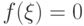 (см. рис. 3.12в).
(см. рис. 3.12в).