Задачи высшей математики с Maxima
3.8.6 Численные методы решения ОДУ
Однако в ряде случаев отыскать символьное решение ОДУ в достаточно компактном виде невозможно. В этом случае целесообразно использовать численные методы. Maxima включает пакет расширения dynamics, позволяющий проинтегрировать систему ОДУ методом Рунге-Кутта.
Начиная с версии 5.12, Maxima включает пакет dynamics (его необходимо загружать перед использованием). Помимо метода Рунге- Кутта, пакет dynamics включает ряд функций для построения различных фракталов.
Метод Рунге-Кутта реализует функция 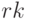 . Синтаксис вызова её вызова:
. Синтаксис вызова её вызова: ![rk([eq], [vars], [init], [t_{range}])](/sites/default/files/tex_cache/01bf338e74a170227639031a88bfe425.png) , где
, где 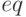 — список правых частей уравнений;
— список правых частей уравнений; 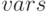 — список зависимых переменных;
— список зависимых переменных; 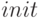 — список начальных значений;
— список начальных значений;  — список
— список ![[t,t_0,t_{end},ht]](/sites/default/files/tex_cache/688d0b49ab7b09a4acc28228ba345757.png) , содержащий символьное обозначение независимой переменной
, содержащий символьное обозначение независимой переменной  , её начальное значение
, её начальное значение  , конечное значение
, конечное значение  , шаг интегрирования
, шаг интегрирования  .
.
Пример:
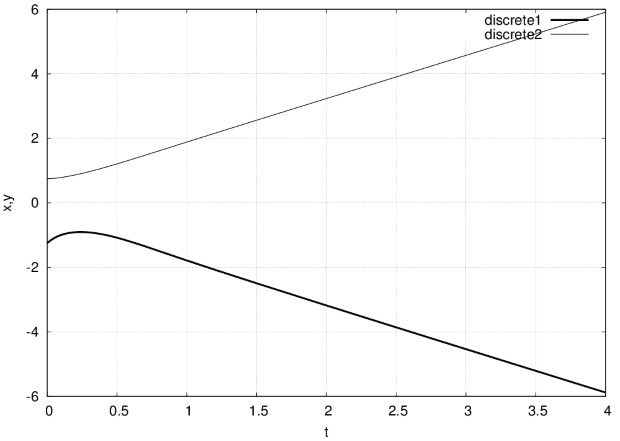
Решить ОДУ

![t = [0\dots4],\ x(0)=-1,25,\ y(0)=0,75](/sites/default/files/tex_cache/d2cdbb2ba6ea6d54ca50d5b183f2256e.png) .
.Используем пакет dynamics.
(%i1) load(''dynamics'')$Выбираем шаг интегрирования 0,02.
(%i2) sol:rk([4*x^2-4*y^2,y^2-x^2+1],[x,y], [-1.25,0.75],[t,0,4,0.02]);
В результате решения получаем список значений в формате [[ ]].
]].
(%i1) load("dynamics")$
(%i2) rp1:4*x^2-4*y^2;
(%i3) rp2:y^2-x^2+1;

(%i4) sol:rk([rp1,rp2],[x,y],[-1.25,0.75],[t,0,4,0.02])$
Список  не выводим на экран (он достаточно длинный, поэтому завершаем ввод команды символом $).
не выводим на экран (он достаточно длинный, поэтому завершаем ввод команды символом $).
Для построения графика решения преобразуем полученный список, построив отдельно список значений 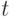 (список
(список 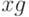 в примере),
в примере), 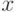 (список
(список  ),
), 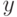 (список
(список  ). При построении графика используем опцию
). При построении графика используем опцию  .
.
(%i5) len:length(sol);

(%i6) xg:makelist(sol[k][1],k,1,len)$ (%i7) yg1:makelist(sol[k][2],k,1,len)$ (%i8) yg2:makelist(sol[k][3],k,1,len)$ (%i9) plot2d([[discrete,xg,yg1],[discrete,xg,yg2]]);
Результат решения представлен на рис. 3.16
Аналогичный, хотя и несколько более сложный пример — моделирование аттрактора Лоренца.
3.9 Ряды Фурье по ортогональным системам
Пакет Мaxima включает достаточно широкие возможности для работы как с классическими тригонометрическими рядами Фурье, так и с рядами Фурье по другим ортогональным системам. Рассмотрим краткое введение, необходимое для понимания приводимых примеров.
3.9.1 Понятие ряда Фурье
Пусть даны две функции  и
и 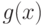 , произведение которых интегрируемо на отрезке [
, произведение которых интегрируемо на отрезке [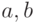 ]. Функции
]. Функции  и
и 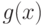 , называются ортогональными на [
, называются ортогональными на [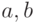 ], если выполняется условие
], если выполняется условие
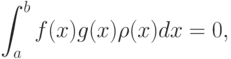
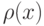 — весовая функция.
— весовая функция.Функциональная последовательность 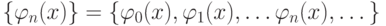 называется ортогональной на [
называется ортогональной на [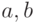 ], если выполняется условие:
], если выполняется условие:

Функциональная последовательность  называется ортонормированной на [
называется ортонормированной на [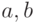 ], если
], если
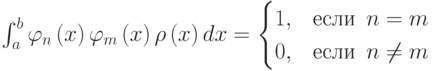
Часто используемая последовательность из тригонометрических функций  . ортогональна на отрезке
. ортогональна на отрезке ![[-\pi ,\pi]](/sites/default/files/tex_cache/085cb9bbd3ce3b289d79e57ad9dfa3ea.png) с весовой функцией
с весовой функцией 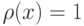 .
.
Проверим свойство ортогональности, вычисляя соответствующие интегралы. При 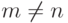 получаем:
получаем:

Если же  , то
, то
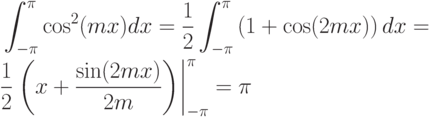
Следовательно,  .. Аналогичным образом устанавливаем, что
.. Аналогичным образом устанавливаем, что  ..
..
Остаётся вычислить интеграл 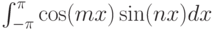 ..
..
Поскольку подинтегральная функция является нечётной, то

Как следует из приведённых равенств, любые две различные функции тригонометрической последовательности ортогональны на отрезке ![[-\pi ,\pi]](/sites/default/files/tex_cache/085cb9bbd3ce3b289d79e57ad9dfa3ea.png) .
.
Другой широко используемой последовательностью ортогональный функций является последовательность полиномов Лежандра. Полином Лежандра степени n можно представить через формулу Родрига в виде:
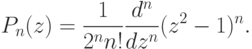
Они также могут быть вычислены по рекуррентной формуле:

Полиномы Лежандра ортогональны на отрезке [-1, 1] с весом 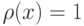 :
:

Ещё одной важной последовательностью ортогональных функций является последовательность полиномов Чебышёва. Полиномы Чебышёва первого рода 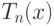 степени n можно определить с помощью равенства:
степени n можно определить с помощью равенства:
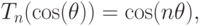
или, что почти эквивалентно,

Они также могут быть вычислены по рекуррентной формуле:

Полиномы Чебышёва ортогональны на отрезке [-1, 1] с весом 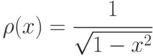 :
:
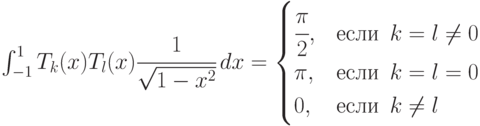
3.9.2 Вычисление коэффициентов тригонометрических рядов Фурье
Члены тригонометрического ряда

 , поэтому и сумма этого ряда
, поэтому и сумма этого ряда  также будет периодической функцией с периодом
также будет периодической функцией с периодом  .
.Предположим, что  –периодическую функцию
–периодическую функцию  можно разложить в тригонометрический ряд, равномерно сходящийся на отрезке
можно разложить в тригонометрический ряд, равномерно сходящийся на отрезке ![[-\pi, \pi]](/sites/default/files/tex_cache/86f9a3a2cc344b78b146c202b2226bae.png) .
.
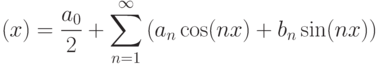 |
( 3.1) |
Рассмотрим вопрос об определении коэффициентов  и
и 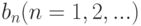 . Для этого применим теорему о почленном интегрировании функционального ряда. Проинтегрируем обе части равенства в пределах от
. Для этого применим теорему о почленном интегрировании функционального ряда. Проинтегрируем обе части равенства в пределах от 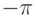 до
до 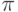 :
:
![\[\int _{-\pi }^{\pi }f\left(x\right)dx=\frac{a_{0} }{2} \int _{-\pi }^{\pi
}dx+\sum _{n=1}^{\infty }\left(a_{n} \int _{-\pi }^{\pi }\cos (nx)dx+b_{n} \int
_{-\pi }^{\pi }\sin (nx)dx \right) .\]](/sites/default/files/tex_cache/62562202903cebff8b6f8733dcff1c94.png)
Из результатов вычисления интегралов, приведённых выше, следует, что все слагаемые, встречающиеся в правой части под знаком суммы равны нулю, поэтому
![\[\int _{-\pi }^{\pi }f(x)dx=\pi a_{0} .\]](/sites/default/files/tex_cache/5178f3ca08d08463003c603f8214ea94.png)
Следовательно,
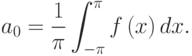 |
( 3.2) |
Для того чтобы найти 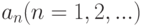 , обе части этого равенства умножим на cos(mx) и проинтегрируем на отрезке
, обе части этого равенства умножим на cos(mx) и проинтегрируем на отрезке ![[-\pi,\pi]](/sites/default/files/tex_cache/a5d4b5c6dcadd17bce3289ba1891d927.png) . Поскольку система тригонометрических функций ортогональна, то
. Поскольку система тригонометрических функций ортогональна, то
![\[\int _{-\pi }^{\pi }\cos (mx)\cos (nx)dx=0,\ \ \int _{-\pi }^{\pi }\cos
(mx)\sin (nx)dx=0 \]](/sites/default/files/tex_cache/77469358e65fa23bf53bc380d369bfb8.png)
 , если
, если 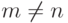 .
.Это означает что все с интегралы, встречающиеся в правой части, будут равны нулю, исключение составляет интеграл, который получается при  . Этот интеграл равен
. Этот интеграл равен 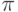 . Поэтому
. Поэтому
![\[\int _{-\pi }^{\pi }f\left(x\right)\cos (nx)dx=a_{n} \int _{-\pi }^{\pi }\cos
^{2} (nx)dx=\pi a_{n} ,\]](/sites/default/files/tex_cache/314f1de4cf5a3fdc5c833647d0e92430.png)

Аналогично, умножив обе части равенства на 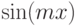 и проинтегрировав на отрезке
и проинтегрировав на отрезке ![[-\pi; \pi]](/sites/default/files/tex_cache/59c9cb397e96086b5e4a2e4804d7af92.png) , получаем, что
, получаем, что 
Итак, если функцию  можно представить в виде тригонометрического ряда, то коэффициенты
можно представить в виде тригонометрического ряда, то коэффициенты  вычисляются по приведённым формулам и называются коэффициентами Фурье для функции
вычисляются по приведённым формулам и называются коэффициентами Фурье для функции  (а ряд — соответственно рядом Фурье для
(а ряд — соответственно рядом Фурье для  ).
).
Промежуток интегрирования ![[-\pi,\pi]](/sites/default/files/tex_cache/a5d4b5c6dcadd17bce3289ba1891d927.png) для периодической с периодом
для периодической с периодом 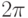 функции можно заменить любым промежутком
функции можно заменить любым промежутком ![[a,a + 2\pi]](/sites/default/files/tex_cache/045929d59bfa37a3a0219b3bd7db302b.png) ,
,  , длина которого равна
, длина которого равна 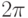 .
.
Функция  называется кусочно-гладкой на отрезке [
называется кусочно-гладкой на отрезке [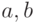 ] если функция
] если функция  и её производная на [
и её производная на [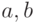 ] имеют конечное число точек разрыва первого рода.
] имеют конечное число точек разрыва первого рода.
Достаточные условия разложимости функции в ряд Фурье даёт теорема Дирихле: если  — периодическая с периодом
— периодическая с периодом 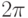 кусочногладкая на
кусочногладкая на ![[-\pi; \pi]](/sites/default/files/tex_cache/59c9cb397e96086b5e4a2e4804d7af92.png) функция, то её ряд Фурье сходится в любой точке этого отрезка и его сумма равна:
функция, то её ряд Фурье сходится в любой точке этого отрезка и его сумма равна:
- значению функции
 , когда
, когда 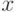 — точка непрерывности функции
— точка непрерывности функции  ;
; -
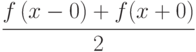 , когда
, когда  — точка разрыва функции
— точка разрыва функции  , при этом
, при этом
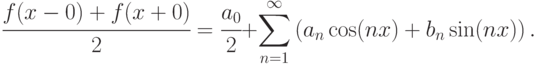
Отметим, что на практике чаще всего встречаются функции, которые удовлетворяют условиям теоремы Дирихле.
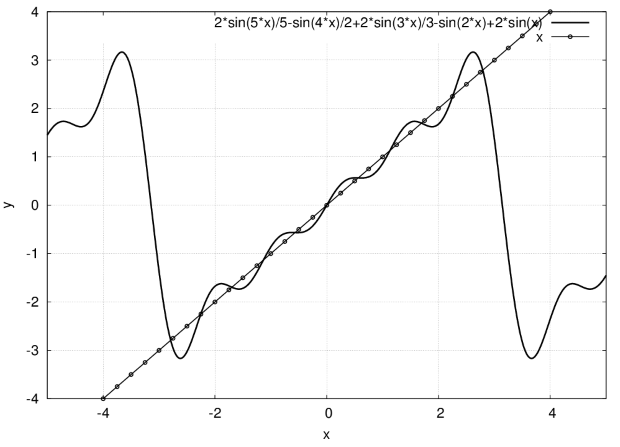
Пример: периодическую с периодом  функцию
функцию 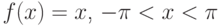 разложить в ряд Фурье.
разложить в ряд Фурье.
Вычислим коэффициенты Фурье (используем Maxima):
(%i1) n:5;

(%i2) f(x):=x;

(%i3) a0:1/%pi*integrate(f(x),x,-%pi,%pi);

(%i4) for k:1 thru n do a[k]:1/%pi*integrate(f(x)*cos(k*x),x,-%pi,%pi);

(%i5) for k:1 thru n do b[k]:1/%pi*integrate(f(x)*sin(k*x),x,-%pi,%pi);

(%i6) for k:1 thru n do display(a[k],b[k]);


(%i7) fun(x):=a0/2+sum(a[k]*cos(k*x),k,1,n)+sum(b[k]*sin(k*x),k,1,n);
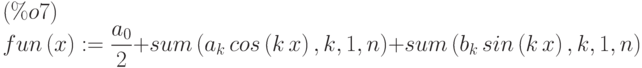
(%i8) wxplot2d([f(x),fun(x)], [x,-5,5], [nticks,20]);
Данная функция  удовлетворяет условиям теоремы Дирихле, её график в сравнении с графиком частичной суммы ряда Фурье
удовлетворяет условиям теоремы Дирихле, её график в сравнении с графиком частичной суммы ряда Фурье 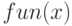 изображён на рис. 3.17.
изображён на рис. 3.17.
3.9.3 Ряды Фурье для чётных и нечётных функций
Предположим, что  — нечётная
— нечётная 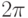 –периодическая функция. В этом случае
–периодическая функция. В этом случае  — чётная функция, поскольку верно равенство
— чётная функция, поскольку верно равенство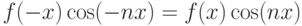 , a
, a  — нечётная функция, так как
— нечётная функция, так как  Поэтому коэффициент ряда Фурье
Поэтому коэффициент ряда Фурье 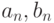 равны:
равны:
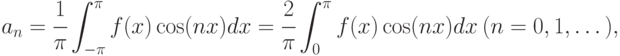

Следовательно, ряд Фурье чётной функции содержит только косинусы, т.е. 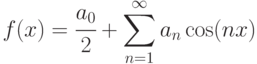 .. Аналогично, если
.. Аналогично, если  — нечётная функция, то
— нечётная функция, то  — нечётная, а
— нечётная, а  — чётная функция.
— чётная функция.
Поэтому 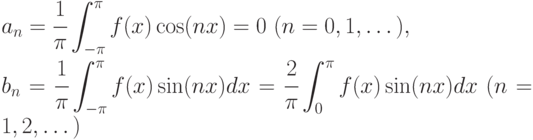
Следовательно, ряд Фурье нечётной функции содержит только синусы, т.е.  .
.
Пример: Разложить в ряд Фурье периодическую с периодом  функцию, заданную на отрезке
функцию, заданную на отрезке ![[-\pi,\pi]](/sites/default/files/tex_cache/a5d4b5c6dcadd17bce3289ba1891d927.png) равенством
равенством  .
.
увеличить изображение
Рис. 3.18. График функции (точки) и суммы первых пяти членов ряда Фурье (сплошная линия)
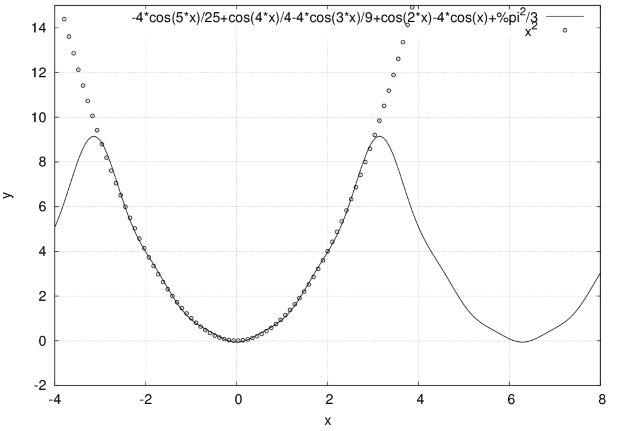
Данная функция 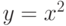 является чётной (рис. 3.18), поэтому её ряд Фурье содержит только косинусы. Вычисляем коэффициенты этого ряда:
является чётной (рис. 3.18), поэтому её ряд Фурье содержит только косинусы. Вычисляем коэффициенты этого ряда: 
Для вычисления коэффициентов 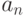 ряда Фурье создаём функцию
ряда Фурье создаём функцию 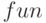 , входными параметрами которой являются имя независимой переменной (в примере это
, входными параметрами которой являются имя независимой переменной (в примере это 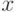 ), число суммируемых членов ряда (
), число суммируемых членов ряда (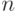 , в дальнейшем функция вызывается при
, в дальнейшем функция вызывается при 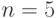 ) и символьное выражение, определяющее функцию, для которой строится разложение (
) и символьное выражение, определяющее функцию, для которой строится разложение ( , функция
, функция 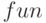 вызывается с
вызывается с 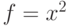 ).
).

(%i1) fun(x,n,f):=(for k:0 thru n do a[k]:1/%pi*integrate(f*cos(k*x),x,-%pi,%pi), a[0]/2 +sum(a[k]*cos(k*x),k,1,n))$
(%i2) fun(x,5,x^2);

Для аналитического вычисления коэффициентов ряда Фурье функции  функцию
функцию 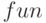 необходимо немного изменить, предусмотрев различные выражения для подинтегрального выражения на полуинтервалах
необходимо немного изменить, предусмотрев различные выражения для подинтегрального выражения на полуинтервалах ![[-\pi, 0) и (0,\pi]](/sites/default/files/tex_cache/55c86548df17c4e7153f4f02d1cffad4.png) (выражения
(выражения  и
и  в списке параметров функции). Текст программы на макроязыке Maxima:
в списке параметров функции). Текст программы на макроязыке Maxima:
fun12(x,n,f1,f2):=(for k:0 thru n do a[k]:1/%pi*(integrate(f1*cos(k*x),x,-%pi,0)+ integrate(f2*cos(k*x),x,0,%pi)), a[0]/2+sum(a[k]*cos(k*x),k,1,n))$
увеличить изображение
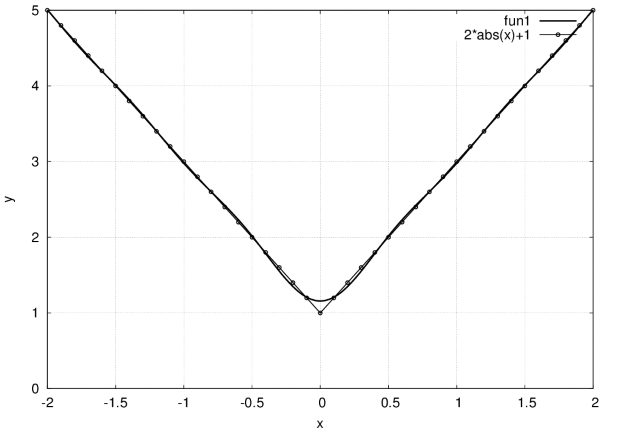
Рис. 3.19. График функции y = |x| (точки) и суммы первых пяти членов ряда Фурье (сплошная линия)
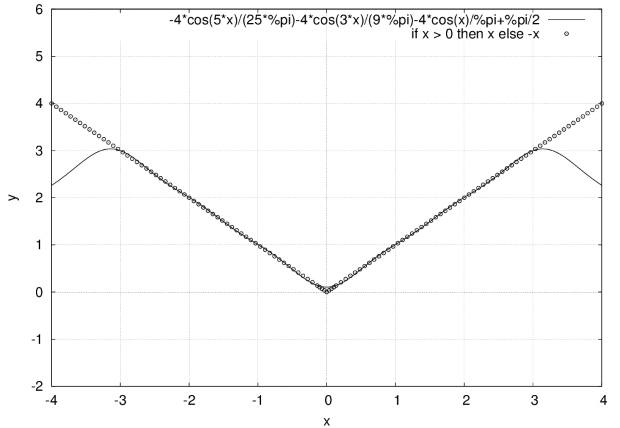
Функция является  также является чётной (рис. 3.19), поэтому её ряд Фурье содержит только косинусы.
также является чётной (рис. 3.19), поэтому её ряд Фурье содержит только косинусы.
Результаты вычисления коэффициентов ряда Фурье для этой функции:
(%i1) fun12(x,5,-x,x);
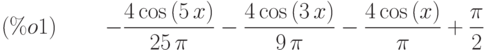
Для построения графика функции  создаём функцию
создаём функцию  , которая использована для построения графика на рис. 3.19.
, которая использована для построения графика на рис. 3.19.
(%i3) fg(x):=if x>0 then x else -x$
3.9.4 Разложение функций в ряд Фурье на отрезке [0,π]
Пусть  определена на отрезке
определена на отрезке ![[0,\pi]](/sites/default/files/tex_cache/a79560c6f70853be01bb23f7539e168c.png) . Для того, чтобы функцию
. Для того, чтобы функцию  разложить в ряд Фурье на этом отрезке, доопределим эту функцию произвольным образом на интервале
разложить в ряд Фурье на этом отрезке, доопределим эту функцию произвольным образом на интервале ![[-\pi, 0]](/sites/default/files/tex_cache/f92fce7cbe481198577892cdabf66462.png) . Рассмотрим два случая:
. Рассмотрим два случая:
Функцию  , заданную на
, заданную на ![[0,\pi]](/sites/default/files/tex_cache/a79560c6f70853be01bb23f7539e168c.png) , продолжим на интервал
, продолжим на интервал ![[-\pi, 0]](/sites/default/files/tex_cache/f92fce7cbe481198577892cdabf66462.png) так, что вновь полученная функция
так, что вновь полученная функция 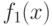 , была чётной:
, была чётной:
![f_{1} = \begin{cases}
f(-x), &\mbox{если } \, x\in [-\pi ,0] \\
f(x), &\mbox{если } \, x\in [0,\pi ]
\end{cases}.](/sites/default/files/tex_cache/65fb239b8cdc20558d134c3466410c60.png)
В таком случае говорят, что  продолжена на
продолжена на ![[-\pi, 0]](/sites/default/files/tex_cache/f92fce7cbe481198577892cdabf66462.png) чётным образом. Поскольку
чётным образом. Поскольку 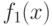 — чётная на
— чётная на ![[-\pi,\pi]](/sites/default/files/tex_cache/a5d4b5c6dcadd17bce3289ba1891d927.png) функция, то её ряд Фурье содержит только косинусы:
функция, то её ряд Фурье содержит только косинусы:
![\[f_{1} (x)=\frac{a_{0} }{2} +\sum _{n=1}^{\infty }a_{n} \cos (nx).\]](/sites/default/files/tex_cache/1c9ee5271d5b273946c4b7b6f7e8e569.png)
Поскольку на отрезке ![[0,\pi]](/sites/default/files/tex_cache/a79560c6f70853be01bb23f7539e168c.png) имеет место равенство
имеет место равенство 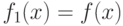 , то ряд Фурье для функции
, то ряд Фурье для функции 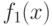 будет и рядом Фурье для
будет и рядом Фурье для  на
на ![[0,\pi]](/sites/default/files/tex_cache/a79560c6f70853be01bb23f7539e168c.png)
Функцию  , заданную на
, заданную на ![[0,\pi]](/sites/default/files/tex_cache/a79560c6f70853be01bb23f7539e168c.png) , продолжим на интервал
, продолжим на интервал ![[-\pi, 0]](/sites/default/files/tex_cache/f92fce7cbe481198577892cdabf66462.png) нечётным образом:
нечётным образом:
![f_{2} = \begin{cases}
-f(-x), &\mbox{если } \, x\in [-\pi ,0[ \\
f(x), &\mbox{если } \, x\in [0,\pi]
\end{cases}.](/sites/default/files/tex_cache/2f66596044f24b6ecf106bc147ebd603.png)
Поскольку 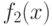 — нечётная на
— нечётная на ![[-\pi,\pi]](/sites/default/files/tex_cache/a5d4b5c6dcadd17bce3289ba1891d927.png) функция, то её ряд Фурье содержит только синусы:
функция, то её ряд Фурье содержит только синусы:
![\[f_{2} (x)=\sum _{n=1}^{\infty }b_{n} \sin (nx).\]](/sites/default/files/tex_cache/531bb372989f9ea28d5a6e3a23a0f20c.png)
Так как 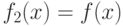 при
при ![\forall x\in [0,\pi]](/sites/default/files/tex_cache/31b6a42d469c51ed61caff0eb51db855.png) , то полученный ряд Фурье для
, то полученный ряд Фурье для 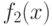 и будет рядом Фурье для
и будет рядом Фурье для  на
на ![[0,\pi]](/sites/default/files/tex_cache/a79560c6f70853be01bb23f7539e168c.png) .
.
Пример: Функцию 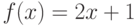 , определённую на отрезке
, определённую на отрезке ![[0,\pi]](/sites/default/files/tex_cache/a79560c6f70853be01bb23f7539e168c.png) , разложить в ряд Фурье: 1)по косинусам; 2)по синусам.
, разложить в ряд Фурье: 1)по косинусам; 2)по синусам.
1) Функцию  продолжим на
продолжим на ![[-\pi, 0]](/sites/default/files/tex_cache/f92fce7cbe481198577892cdabf66462.png) чётным образом, т.е. составим новую функцию
чётным образом, т.е. составим новую функцию 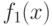 по формуле:
по формуле:
![f_{1}(x) = \begin{cases}
-2x+1, &\mbox{если } \, x\in [-\pi ,0[ \\
2x+1, &\mbox{если } \, x\in [0,\pi]
\end{cases}.](/sites/default/files/tex_cache/ff27c3a02d9e0a1fac4d5ba5e834b53c.png)
Вычисляем коэффициенты Фурье для этой функции при помощи функции  :
:
(%i1) fleft:-2*x+1;

(%i2 fright:2*x+1;
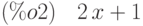
(%i3) funcos(x,7,fleft,fright);
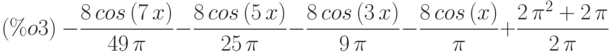
увеличить изображение
Рис. 3.20. График функции y = 2x+1, продолженной чётным образом, и суммы семи членов соответствующего ряда
Графическое сопоставление результатов суммирования ряда Фурье и аналитического выражения заданной функции представлены на рис. 3.20
2) Функцию  продолжим на
продолжим на ![[-\pi, 0]](/sites/default/files/tex_cache/f92fce7cbe481198577892cdabf66462.png) нечётным образом. Составим новую функцию
нечётным образом. Составим новую функцию 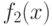 по формуле
по формуле ![f_{2} (x)=\left\{_{2x+1,\ x\in [0,\pi]}^{2x-1,\ x\in [-\pi ,0[} \right.](/sites/default/files/tex_cache/a48ceec3068cc9624396cc351f2bcbd1.png)
Вычислим коэффициенты Фурье для этой функции, используя функцию  , аналогичную приведённой выше.
, аналогичную приведённой выше.
Пример:
(%i1) fleft:2*x-1$ (%i2) fright:2*x+1$ (%i3) f(x):=(if x>0 then fright else fleft)$ (%i4) fun12sin(x,n,f1,f2):=(for k:1 thru n do b[k]:1/%pi*(integrate(f1*sin(k*x),x,-%pi,0) +integrate(f2*sin(k*x),x,0,%pi)), sum(b[k]*sin(k*x),k,1,n))$ (%i5) fun12sin(x,7,fleft,fright);
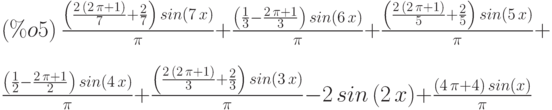
Графическое сопоставление результатов суммирования ряда Фурье и аналитического выражения заданной функции представлены на рис. 3.21
увеличить изображение
Рис. 3.21. Сравнение графика функции y = 2x + 1 при нечётном продолжении и суммы семи членов соответствующего ряда Фурье