НОУ ИНТУИТ | Компьютерная математика с Maxima. Лекция 7: Решение физических и математических задач с Maxima

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 24.03.2015 | Доступ: свободный | Студентов: 553 / 138 | Длительность: 19:00:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Ключевые слова: сеть, Интернет

Доступная литература и сеть Интернет в качестве "электронного помощника" студентов и школьников обычно позиционирует пакет MathCad, изредка — Maple или Mathematica. Материал данной главы содержит ряд разнородных задач, которые решались разными авторами вручную или при помощи MathCad.

7.1 Операции с полиномами и рациональными функциями

Рассмотрим решение с помощью Maxima нескольких задач из классического сборника под редакцией М.И. Сканави. В Maxima "пошаговое" упрощение выражений с последовательным использованием стандартного набора примитивов (формул суммы или разности кубов, формул возведения суммы или разности в степень и т.п.) выполнить сложно, поэтому результат являются фактически справочным, на который следует ориентироваться при решении вручную, при помощи ручки и бумаги.

7.1.1 Упрощение алгебраических выражений

Пример:

Упростить выражение и вычислить его, если даны числовые значения параметров:

(%i1)	g:(1/a-1/(b+c))/(1/a+1/(b+c))*(1+(b^2+c^2-a^2)/2/b/c)/((a-b-c)/a/b/c);

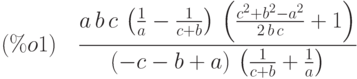
$(\%o1)\quad \frac{a\,b\,c\,\left( \frac{1}{a}-\frac{1}{c+b}\right) \,\left( \frac{{c}^{2}+{b}^{2}-{a}^{2}}{2\,b\,c}+1\right) }{\left( -c-b+a\right) \,\left( \frac{1}{c+b}+\frac{1}{a}\right) }$$

(%i2)	ratsimp(%);

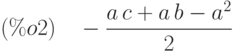
$(\%o2)\quad -\frac{a\,c+a\,b-{a}^{2}}{2}$

(%i3)	%,a=0.02,b=-11.05,c=1.07;

$(\%o3)\quad 0.1$

Пример: Упростить выражение и вычислить его, если даны числовые значения параметров:

(%i1)	(sqrt(x)+1)/(x*sqrt(x)+x+sqrt(x))/(1/(x^2-sqrt(x)));

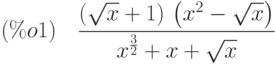
$(\%o1)\quad \frac{\left( \sqrt{x}+1\right) \,\left( {x}^{2}-\sqrt{x}\right) }{{x}^{\frac{3}{2}}+x+\sqrt{x}}$

(%i2)	ratsimp(%);

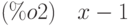
$(\%o2)\quad x-1$

Пример: Сделать указанную подстановку и результат упростить:

(%i3)	expr:(x^3-a^(-2/3)*b^(-1)*(a^2+b^2)*x+b^(1/2))/(b^(3/2)*x^2);

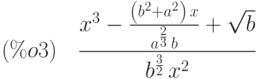
$(\%o3)\quad \frac{{x}^{3}-\frac{\left( {b}^{2}+{a}^{2}\right) \,x}{{a}^{\frac{2}{3}}\,b}+\sqrt{b}}{{b}^{\frac{3}{2}}\,{x}^{2}}$

(%i4)	ratsimp(%);

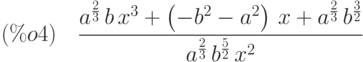
$(\%o4)\quad \frac{{a}^{\frac{2}{3}}\,b\,{x}^{3}+\left( -{b}^{2}-{a}^{2}\right) \,x+{a}^{\frac{2}{3}}\,{b}^{\frac{3}{2}}}{{a}^{\frac{2}{3}}\,{b}^{\frac{5}{2}}\,{x}^{2}}$

(%i5)	radcan(%);

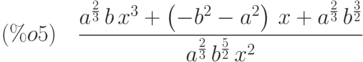
$(\%o5)\quad \frac{{a}^{\frac{2}{3}}\,b\,{x}^{3}+\left( -{b}^{2}-{a}^{2}\right) \,x+{a}^{\frac{2}{3}}\,{b}^{\frac{3}{2}}}{{a}^{\frac{2}{3}}\,{b}^{\frac{5}{2}}\,{x}^{2}}$

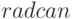Без указанной подстановки упрощение посредством комбинации функций ratsimp и radcan не удаётся.

(%i6)	%,x=a^(2/3)*b^(-1/2);

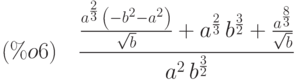
$(\%o6)\quad \frac{\frac{{a}^{\frac{2}{3}}\,\left( -{b}^{2}-{a}^{2}\right) }{\sqrt{b}}+{a}^{\frac{2}{3}}\,{b}^{\frac{3}{2}}+\frac{{a}^{\frac{8}{3}}}{\sqrt{b}}}{{a}^{2}\,{b}^{\frac{3}{2}}}$

(%i7)	ratsimp(%);

Конечный результат оказывается простым

$(\%o7)\quad 0$

7.1.2 Разложение полиномов и рациональных выражений на множители

7.1.2.1 Решение алгебраических уравнений

Maxima (как и любой другой пакет символьной математики) не всегда способен получить окончательное решение. Однако полученный результат может оказаться всё же проще, чем исходная задача.

Пример (также из сборника под ред. М.И. Сканави): Решить уравнение 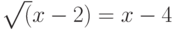$\sqrt(x-2) = x-4$ :

(%i1)	solve([sqrt(x-2)=x-4],[x]);

$(\%o1)\quad [x=\sqrt{x-2}+4]$

Уравнение имеет одно решение: 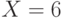X = 6 , однако для отыскания его с помощью Maxima придётся прибегнуть к замене исходного уравнения его следствием:

(%i3)	solve([(x-2)=(x-4)^2],[x]);

$(\%o3)\quad [x=6,x=3]$

Решения для дальнейшего использования можно извлечь из списка функцией :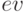

(%i1)	sol:solve([x-2=(x-4)^2],[x]);

$(\%o1)\quad [x=6,x=3]$

(%i2)	ev(x,sol[1]);

$(\%o2)\quad 6$

(%i3)	ev(x,sol[2]);

$(\%o3)\quad 3$

Ещё два примера решения алгебраических уравнений:

(%i1)	eq:7*(x+1/x)-2*(x^2+1/x^2)=9;

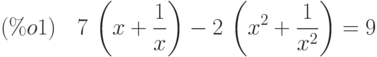
$(\%o1)\quad 7\,\left( x+\frac{1}{x}\right) -2\,\left( {x}^{2}+\frac{1}{{x}^{2}}\right) =9$

(%i2)	sol:solve([eq],[x]);

$(\%o2)\quad [x=2,x=\frac{1}{2},x=-\frac{\sqrt{3}\,i-1}{2},x=\frac{\sqrt{3}\,i+1}{2}]$

(%i3)	x1:ev(x,sol[1]); x2:ev(x,sol[2]);
/*комплексные корни не рассматриваем*/

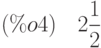
$(\%o4)\quad 2\frac{1}{2}$

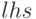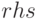Уравнения с радикалами перед решением в Maxima приходится преобразовывать к степенной форме (для выделения левой и правой части выражения используют функции lhs и rhs соответственно):

(%i1)	eq:sqrt(x+1)+sqrt(4*x+13)=sqrt(3*x+12);

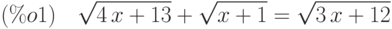
$(\%o1)\quad \sqrt{4\,x+13}+\sqrt{x+1}=\sqrt{3\,x+12}$

(%i2)	eq1:lhs(eq)^2=rhs(eq)^2;

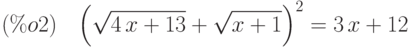
$(\%o2)\quad {\left( \sqrt{4\,x+13}+\sqrt{x+1}\right) }^{2}=3\,x+12$

(%i3)	solve([eq1],[x]);

$(\%o3)\quad [x=-\sqrt{x+1}\,\sqrt{4\,x+13}-1]$

(%i4)	eq2:x+1=rhs(%[1])+1;

$(\%o4)\quad x+1=-\sqrt{x+1}\,\sqrt{4\,x+13}$

(%i5)	eq3:lhs(eq2)^2=rhs(eq2)^2;

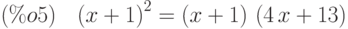
$(\%o5)\quad {\left( x+1\right) }^{2}=\left( x+1\right) \,\left( 4\,x+13\right)$

Последняя команда позволила получить степенное уравнение, разрешимое аналитически в Maxima (для этого потребовалось дважды возвести в квадрат исходное уравнение).

(%i6)	solve([eq3],[x]);

$(\%o6)\quad [x=-4,x=-1]$

Проверку решения выполняем при помощи функции .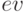

Решение 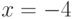x = -4 не удовлетворяет исходному уравнению.

(%i7)	ev(eq,%[1]);

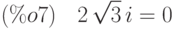
$(\%o7)\quad 2\,\sqrt{3}\,i=0$

Решение 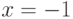x = -1 превращает исходное уравнение в верное равенство:

(%i8)	ev(eq,%o6[2]);

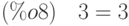
$(\%o8)\quad 3=3$

Рассмотрим ещё один пример, иллюстрирующий замену и подстановку при решении алгебраических уравнений:

(%i1)	eq:sqrt(x+3-4*sqrt(x-1))+sqrt(x+8-6*sqrt(x-1))=1;

Исходное уравнение:

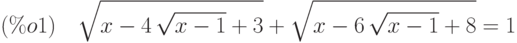
$(\%o1)\quad \sqrt{x-4\,\sqrt{x-1}+3}+\sqrt{x-6\,\sqrt{x-1}+8}=1$

Выполним замену 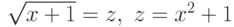$\sqrt{x+1}=z,\ z=x^2 + 1$

(%i2)	eq1:subst(z,sqrt(x-1),eq);

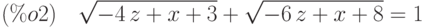
$(\%o2)\quad \sqrt{-4\,z+x+3}+\sqrt{-6\,z+x+8}=1$

(%i3)	eq2:subst(z^2+1,x,eq1);

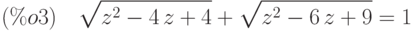
$(\%o3)\quad \sqrt{{z}^{2}-4\,z+4}+\sqrt{{z}^{2}-6\,z+9}=1$

Упрощаем полученный результат:

(%i4)	radcan(%);

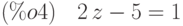
$(\%o4)\quad 2\,z-5=1$

(%i5)	solve([%],z);

$(\%o5)\quad [z=3]$

(%i6)	solve([sqrt(x-1)=3],[x]);

$(\%o6)\quad [x=10]$

Выполним проверку

(%i7) ev(eq,%[1]);

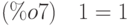
$(\%o7)\quad 1=1$

Значительная часть тригонометрических уравнений школьного курса также разрешимы в Maxima, но непосредственное решение удаётся получить далеко не всегда.

Примеры:

(%i1)	solve([sin(%pi/6-x)=sqrt(3)/2],[x]);
solve: using arc-trig functions to get a solution.
Some solutions will be lost.

$(\%o1)\quad [x=-\frac{\pi }{6}]$

Большинство тригонометрических уравнений в Maxima (кроме простейших) приходится решать приведением их к алгебраическим.

Логарифмические и показательные уравнения также решаются в Maxima путём замены переменных и сведения к алгебраическим (см. выше специфические функции для упрощения логарифмических выражений).

Дальше >>

Авторизоваться

Компьютерная математика с Maxima

Решение физических и математических задач с Maxima

7.1 Операции с полиномами и рациональными функциями

7.1.1 Упрощение алгебраических выражений

7.1.2 Разложение полиномов и рациональных выражений на множители

7.1.2.1 Решение алгебраических уравнений

Вопросы и ответы