| Россия, Москва, МЭИ, 2006 |
Системотехнические аспекты перспективных компьютерных технологий
Синтез комбинационных вентилей из наноструктур проведем на основе конечно-автоматных нановентилей JK- типа. В этом случае будем считать, что виртуальные нановентили, составляющие нанотриггеры JK- типа, получены за счет взаимодействия нанотриггеров D- типа, которые рассматриваются как исходный субнанометровый субстрат.
Абстрактный синтез виртуальных комбинационных нановентилей на нанотриггерах JK- типа может осуществляться одновременно в двух плоскостях наносхемотехнического проекта - "материальной" и "виртуальной", так как он базируется на квантовом субстрате, который не выродился до тавтологии и не потерял свои полезные конечно-автоматные свойства в "материальной" плоскости проекта.
Устранение схемотехнической неоднозначности в реакции таких нановентилей проще всего провести путем модификации "конечно-автоматных" функций нановентилей-прототипов за счет многоместной суперпозиции электромагнитных полей. При этом предполагается, что "тирания связей" в реальных квантовых системах позволяет породить всю совокупность необходимых виртуальных нановентилей.
Во всех вариантах схем устранения неоднозначной схемотехнической реакции ограничим состав "конечно-автоматных" функций возможностями обобщенного триггера JK- типа рис. 7.10 и будем считать: квантовый субстрат реализует только заданную "конечно-автоматную" функцию переключения, а его внутренняя логическая схема изменяется только за счет виртуальных нановентилей;
- процесс взаимодействия электромагнитных полей двух конечно-автоматных квантовых субстратов можно представить виртуальными вентилями типа: "И", "ИЛИ", "НЕРАВНОЗНАЧНОСТЬ" и "ИНВЕРСИЯ";
- суперпозиция электромагнитных полей осуществляется независимо по всем входам-выходам составляющих триггеров JK-типа.
Приводимые ниже логические схемы нанотриггеров JK- типа предполагают:
- минимальные затраты субнановентилей, функционально эквивалентных D-триггерам, что соответствует полному использованию электромагнитных взаимодействий между составляющими субнаноструктурами, то есть полной трансформации всех паразитных взаимодействий субнаноструктур в функционально значимые;
- наличие в них инверсных виртуальных выходов, сформированных дополнительными нанотриггерами D-типа по схеме рис. 7.15-а, которые для упрощения анализа на рисунке не показаны.
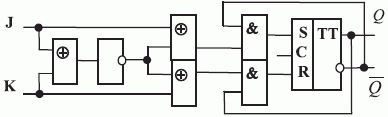
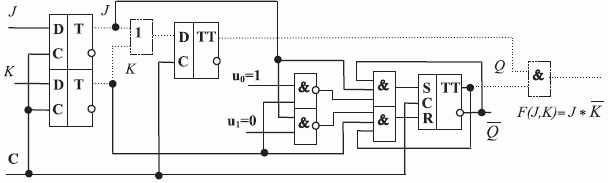
В первом варианте схемы устранения схемотехнической неоднозначности используем нанотриггер классического JK- типа, представив в PD- ассоциативной форме (7.10) реализуемую им "конечно-автоматную" функцию (в табл. 7.3 это JK ).
Форма записи (7.10) в явном виде выделяет переменную Q(t), которая используется в схеме как управляющая и переключает "конечно-автоматный" вентиль с реализации одной функции ![F[J(t),K(t)] = J(t)](/sites/default/files/tex_cache/9d422e3e5cca4d5ed3fd031c07752319.png) (при
(при 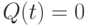 ) на другую
) на другую ![F [J(t),K(t)] = \overline{K(t)}](/sites/default/files/tex_cache/9fd5868d437ee15fe6f54a3729c46415.png) (при
(при 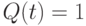 ).
).
Тогда "конечно-автоматную" функцию, реализуемую зеркально симметричным триггером 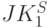 -типа (рис. 7.18), можно записать:
-типа (рис. 7.18), можно записать:
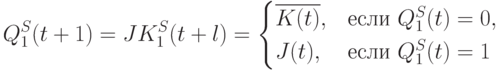 |
( 7.12) |
Из приведенных соотношений и данных табл. 7.5 видно:
- Если входы нанотриггеров
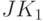 - и
- и 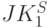 -типов соединены параллельно (рис. 7.19), а сами триггеры находятся в симметричных "нулевых"
-типов соединены параллельно (рис. 7.19), а сами триггеры находятся в симметричных "нулевых" 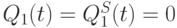 или "единичных"
или "единичных" 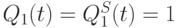 состояниях, то на их выходах с помощью виртуального вентиля "ИЛИ" можно реализовать "комбинационную" базисную логическую функцию вида:
состояниях, то на их выходах с помощью виртуального вентиля "ИЛИ" можно реализовать "комбинационную" базисную логическую функцию вида: ![F[Q_{1}(t),Q^{S}_{1}(t)] = \overline{K(t)* \overline{J(t)}}.](/sites/default/files/tex_cache/984608fa157c9f9157cfb97c6e9abe8b.png)
- Если оба нанотриггера при тех же входных условиях находятся в антисимметричных состояниях
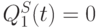 ,
, 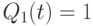 или, наоборот,
или, наоборот, 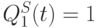 ,
, 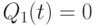 , то на их выходах сохраняется неоднозначная конечно-автоматная реакция при воздействии следующих комбинаций значений входных переменных:
, то на их выходах сохраняется неоднозначная конечно-автоматная реакция при воздействии следующих комбинаций значений входных переменных:  и
и 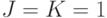 . Отсюда встает задача поддержания такого взаимодействия между классическим и зеркально-симметричным ему нанотриггером
. Отсюда встает задача поддержания такого взаимодействия между классическим и зеркально-симметричным ему нанотриггером 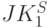 -типа, которое устраняет неоднозначность объединенной по виртуальному "ИЛИ" выходной реакции именно на этих комбинациях состояний нано-триггеров и соответствующих значений входных переменных.
-типа, которое устраняет неоднозначность объединенной по виртуальному "ИЛИ" выходной реакции именно на этих комбинациях состояний нано-триггеров и соответствующих значений входных переменных.
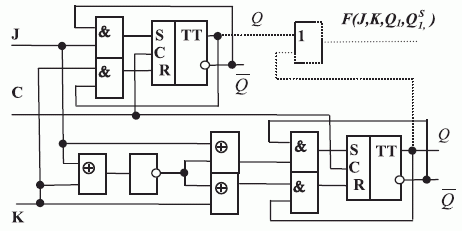
Как и в случае перехода от RS- к JK- триггеру, для устранения такой неоднозначной реакции достаточно ввести "глобальные" обратные связи, но теперь уже между классическим и зеркально симметричным нанотриг-герами JK- типа (рис. 7.20). Такие обратные связи изменяют восприятие соответствующих комбинаций значений промежуточных переменных за счет ассоциативной интерпретации фактических антисимметричных состояний как симметричных.
Согласно данным табл. 7.5 в схеме рис. 7.20:
- виртуальные нановентили "И" активируют ассоциативные обратные связи между нанотриггерами JK-типа, только когда они находятся в антисимметричных состояниях;
- при состоянии всей системы
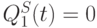 ,
, 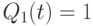 нанотриггер
нанотриггер 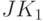 -типа "воспринимает" свое состояние в инверсном виде, что изменяет на противоположную и роль комбинаций входных сигналов
-типа "воспринимает" свое состояние в инверсном виде, что изменяет на противоположную и роль комбинаций входных сигналов 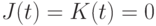 и
и 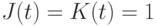 , первая из которых инвертирует предыдущее состояние, а вторая - сохраняет его;
, первая из которых инвертирует предыдущее состояние, а вторая - сохраняет его;
Таблица 7.5. Таблица истинности параллельного соединения JK_1-и JK_1^S-триггеров Базис И - НЕ 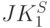

Без обратных связей С обратными связями 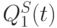
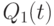
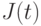
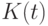
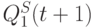
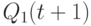
"ИЛИ" "ИЛИ" 0 0 0 0 1 0 1 1 0 0 0 1 0 0 0 0 0 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 0 1 0 1 0 0 0 0 0 1 1 0 1 1 1 1 0 1 1 1 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 0 1 0 0 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 - при состоянии всей системы
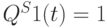 ,
,  теперь уже нано-триггер
теперь уже нано-триггер 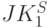 -типа "воспринимает" свое состояние в инверсном виде, что изменяет на противоположную и роль комбинаций входных сигналов
-типа "воспринимает" свое состояние в инверсном виде, что изменяет на противоположную и роль комбинаций входных сигналов 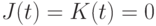 и
и 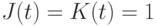 , первая из которых сохраняет предыдущее состояние, а вторая - инвертирует его.
, первая из которых сохраняет предыдущее состояние, а вторая - инвертирует его.
Таким образом, если конечно-автоматные вентили типа 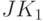 и
и 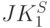 взаимодействуют своими электромагнитными полями так, как показано на рис. 7.20, то их комплекс реализует "комбинационную" базисную функцию
взаимодействуют своими электромагнитными полями так, как показано на рис. 7.20, то их комплекс реализует "комбинационную" базисную функцию ![F [Q _{1}( t),Q ^{S} _{1}(t)] = \overline{K(t)* \overline{J(t)}}](/sites/default/files/tex_cache/12053062d507ea5ddebc3fb381bf5ef7.png) , но каждый из них остается конечным автоматом. Во второй схеме устранения неоднозначной схемотехнической реакции используем два обобщенных триггера, один из которых выполняет преобразование
, но каждый из них остается конечным автоматом. Во второй схеме устранения неоднозначной схемотехнической реакции используем два обобщенных триггера, один из которых выполняет преобразование  , а второй - преобразование
, а второй - преобразование 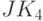 :
:
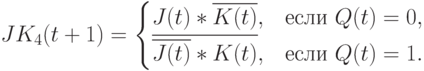
Поведение этого комплекса без образования в нем обратных связей описывает предпоследний столбец табл. 7.6, а при наличии обратных связей и соответствующих виртуальных нановентилей - рис. 7.21 и последний столбец табл. 7.6. В этой схеме использована "глобальная" обратная связь всего комбинационного нановентиля, который реализует базисную функцию ![F[Q_{4}(t),Q_{1}(t)] = J(t)* \overline{K(t)}](/sites/default/files/tex_cache/f45d9b16ad65add1813210dc3ccbd073.png) , если Q- выходы этих нано-триггеров объединить виртуальным "И".
, если Q- выходы этих нано-триггеров объединить виртуальным "И".
| Базис И-НЕ | 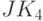 |
 |
Без обратных связей | С обратными связями | |||
|---|---|---|---|---|---|---|---|
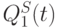 |
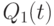 |
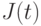 |
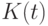 |
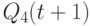 |
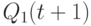 |
"И" | "И" |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Специфика работы схемы рис. 7.21:
- В нанотриггере
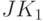 -типа только комбинация состояний
-типа только комбинация состояний 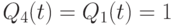 интерпретируется как "единичное" состояние, а комбинация
интерпретируется как "единичное" состояние, а комбинация 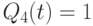 и
и 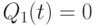 воспринимается как "нулевое" состояние, что создает асимметричный перекос в восприятии собственного "единичного" состояния этого триггера. В результате выходная реакция этого нанотриггера в большей степени отвечает собственному "нулевому" состоянию.
воспринимается как "нулевое" состояние, что создает асимметричный перекос в восприятии собственного "единичного" состояния этого триггера. В результате выходная реакция этого нанотриггера в большей степени отвечает собственному "нулевому" состоянию. - В нанотриггере
 -типа собственные "нулевые" и "единичные" состояния интерпретируются буквально и без каких-либо коррекций в их интерпретации, но при
-типа собственные "нулевые" и "единичные" состояния интерпретируются буквально и без каких-либо коррекций в их интерпретации, но при 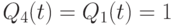 комбинация значений входных переменных
комбинация значений входных переменных 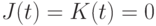 воспринимается как установка в "ноль", то есть как комбинация
воспринимается как установка в "ноль", то есть как комбинация 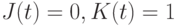 .
.
Рассмотренные схемы виртуальных комбинационных нановентилей используют параллельное соединение исходных "конечно-автоматных" нановентилей, и поэтому их можно отнести к схемам векторного типа.
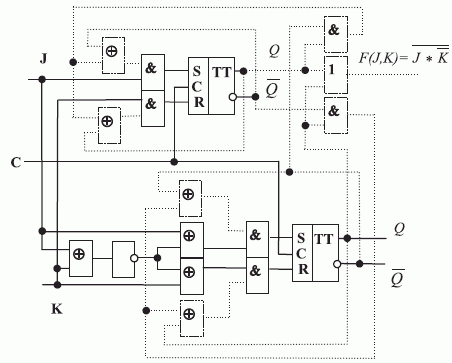
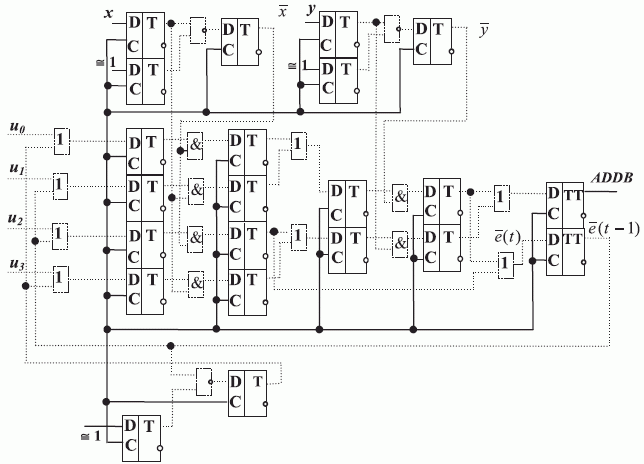
В третьей схеме устранения неоднозначной схемотехнической реакции используем конвейерную (последовательную) схему взаимодействия исходных конечно-автоматных нановентилей, в которой суперпозиция электромагнитных полей формируется как на входах, так и на выходе задающего нановентиля конечно-автоматного типа (рис. 7.22).
В этой схеме JK- триггер настроен на преобразование 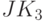 , которое используется как образующее для формирования выходной "комбинационной" логической функции. Образующий JK- триггер взаимодействует своими электромагнитными полями с предшествующими нанотригге-рами D- типа как на входе, так и на выходе нановентиля. В результате на его входе формируется виртуальный вентиль "ИЛИ", который через виртуальный вентиль "И" блокирует выход
, которое используется как образующее для формирования выходной "комбинационной" логической функции. Образующий JK- триггер взаимодействует своими электромагнитными полями с предшествующими нанотригге-рами D- типа как на входе, так и на выходе нановентиля. В результате на его входе формируется виртуальный вентиль "ИЛИ", который через виртуальный вентиль "И" блокирует выход 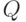 только при
только при 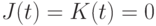 . Такая модификация образующей "конечно-автоматной" функции
. Такая модификация образующей "конечно-автоматной" функции 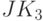 (см. табл. 8.2) приводит ее к виду одной из базисных функций в классе булевых функций:
(см. табл. 8.2) приводит ее к виду одной из базисных функций в классе булевых функций: 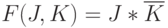 .
.
Конвейерный сумматор является самым "сложным" операционным блоком в МКМД- бит-потоковых вычислительных технологиях, и поэтому он задает архитектуру не только бит-процессора, но и всей вычислительной системы [139]. Для синтеза такого наносумматора на виртуальных нановентилях D- типа воспользуемся PD- ассоциативной формой записи его логических функций, которая в явном виде использует предыдущее значение "единицы переноса" 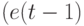 ) в качестве "ассоциативной" управляющей переменной при формировании последующего значения как "суммы" (
) в качестве "ассоциативной" управляющей переменной при формировании последующего значения как "суммы" ( 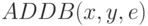 ), так и самой "единицы переноса" (
), так и самой "единицы переноса" (  ).
).
Согласно данным табл. 7.7 бит-операции, которые выполняет конвейерный бит-сумматор, в PD- ассоциативной форме можно записать:
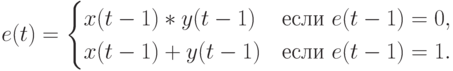 |
( 7.13) |
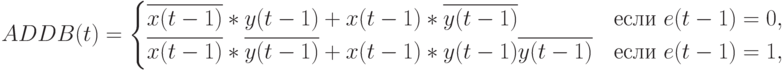 |
( 7.14) |
- где символы (  ), (
), ( 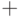 ) и (
) и (  ) соответствуют "И", "ИЛИ" и "НЕ" (инверсии) соответственно.
) соответствуют "И", "ИЛИ" и "НЕ" (инверсии) соответственно.
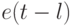
|
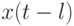
|
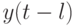
|
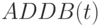
|

|
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
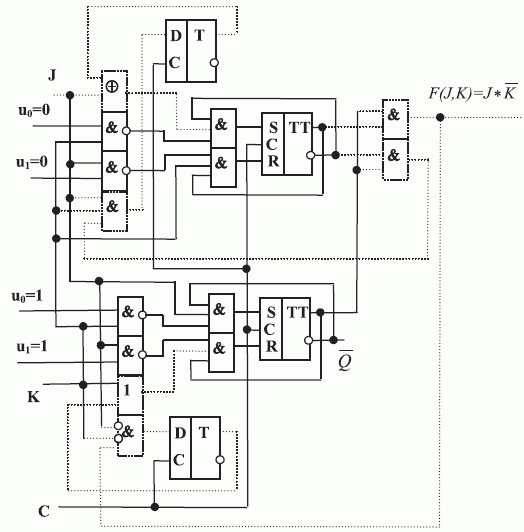
Соотношениям (7.13, 7.14) отвечает схема рис. 7.23. Основу схемы составляет селектор-мультиплексор на четыре мультиплицируемых входа, который используется как универсальный логический модуль [101] в классе булевых функций двух переменных 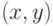 .
.
Настройка такого модуля на требуемую булеву функцию осуществляется фиксацией значений компонент управляющего вектора 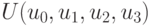 , которые фактически повторяют таблицу истинности реализуемой функции. Чтобы такой бит-потоковый наносумматор перевести из режима реализации конечно-автоматных бит-инструкций в режим реализации булевых функций двух переменных, достаточно заблокировать выходы нанотриггера обратной связи (
, которые фактически повторяют таблицу истинности реализуемой функции. Чтобы такой бит-потоковый наносумматор перевести из режима реализации конечно-автоматных бит-инструкций в режим реализации булевых функций двух переменных, достаточно заблокировать выходы нанотриггера обратной связи ( 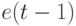 ).
).
Физико-техническое достоинство такой схемы бит-конвейерного наносумматора - это высокая регулярность ее структуры, которая включает три селектора-мультиплексора на два мультиплицируемых входа каждый и три инвертора. Системотехническое достоинство бит-потокового наносумматора состоит в том, что для построения сверхпараллельных МКМД-бит-потоковых вычислителей [139] требуется отработать технологию производства наносхемотехнического узла, содержащего менее сотни нановентилей.