| Россия, Москва, МЭИ, 2006 |
Системотехнические аспекты перспективных компьютерных технологий
Во всех рассмотренных случаях считалось, что основная вычислительная нагрузка ложится на виртуальные комбинационные нановентили, а материальные конечно-автоматные нановентили играют соподчиненную роль. Вместе с тем, дуальная природа квантовых систем позволяет решить и обратную задачу, возложив основную вычислительную нагрузку на материальные "конечно-автоматные" нановентили, модификация функций которых осуществляется с использованием виртуальных комбинационных нановентилей. С этих позиций схему рис. 7.14 можно рассматривать как комбинационный нановентиль с материальным выходом, в котором все вспомогательные субнановентили реализованы на основе дополнительных нанотриггеров D- типа.
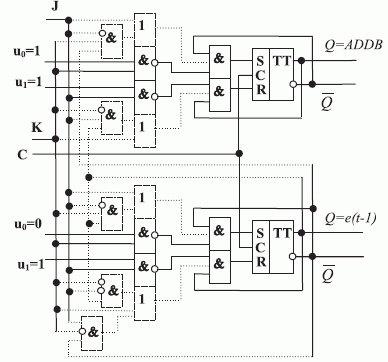
Проиллюстрируем сказанное на примере конвейерного сумматора, в котором используется комплекс из двух обобщенных триггеров JK- типа, один из которых формирует выход "суммы" ( 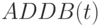 ), а другой - выход "единицы переноса" (
), а другой - выход "единицы переноса" (  ).
).
Из данных таблиц 7.4 и 7.7 видно:
- с ADDB наиболее сходно преобразование
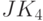 , и поэтому его можно взять в качестве образующего для реализации "суммы";
, и поэтому его можно взять в качестве образующего для реализации "суммы"; - аналогично и для преобразования
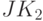 , которое можно взять в качестве образующего для реализации "единицы переноса".
, которое можно взять в качестве образующего для реализации "единицы переноса".
Чтобы преобразование 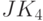 трансформировать в
трансформировать в 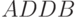 , необходимо при
, необходимо при 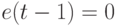 комбинацию значений
комбинацию значений  ) воспринимать как сигнал установки в "единицу", а при
) воспринимать как сигнал установки в "единицу", а при 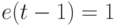 комбинацию (
комбинацию ( 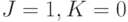 ) - как сигнал установки в "ноль".
) - как сигнал установки в "ноль".
Чтобы преобразование 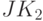 трансформировать в
трансформировать в  ,необходимо:
,необходимо:
- при
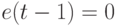 комбинацию значений (
комбинацию значений ( 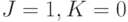 ) воспринимать как сигнал установки в "ноль";
) воспринимать как сигнал установки в "ноль"; - при
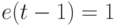 комбинацию значений
комбинацию значений  воспринимать как сигнал установки в "ноль", а комбинацию значений (
воспринимать как сигнал установки в "ноль", а комбинацию значений ( 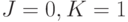 ) - как сигнал установки в "единицу".
) - как сигнал установки в "единицу".
Схема наносумматора на нанотриггерах JK- типа приведена на рис. 7.24, и от наносумматора на нанотриггерах D- типа она отличается меньшим универсализмом, так как не позволяет реализовать все булевы функции двух переменных.
Проведенный абстрактный синтез комбинационных нановентилей и схем на основе детерминированных конечно-автоматных нановентилей показал:
- 1. Материальную основу элементной базы наносхемотехники, полученную эмпирическим путем, можно ограничить триггерами D- типа, которые реализуются квантовыми кластерами и составляют неделимую единицу самого нижнего, субнанометрового уровня схемотехники наноэ-лектронного проекта. Используя композицию нанотриггеров D- типа, порождающую виртуальные нановентили обобщенного нанотриггера JK- типа, можно получить неделимую единицу конечно-автоматного уровня схемотехники наноэлектронного проекта. Используя композицию нанотриггеров JK- и D- типа, можно получить базисные комбинационные вентили, отвечающие требованиям формально-логического синтеза схем классической кремниевой компиляции.
- В реальных условиях синтеза виртуальных комбинационных нано-вентилей составляющие их конечные автоматы способны выполнить закрепленные за ними функции только в контексте описанных взаимодействий, а вне этого контекста необходимо пользоваться их прототипами, которые, будучи размещены в заранее заданные схемы взаимодействия, поведут себя в соответствии с функциональными требованиями ко всему комплексу. Поэтому инструментальные средства нанокомпиляторов должны содержать библиотеки физических прототипов триггеров
 - и
- и 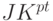 -типов и способов их композиции в комбинационные нановентили.
-типов и способов их композиции в комбинационные нановентили. - Разнообразие и специфика полученных эмпирическим путем прототипов D- наноструктур определяется законами суперпозиции электромагнитных полей, используемых как при конструировании более сложных конечно-автоматных нановентилей, так и при конструировании комбинационных нановентилей. Разнообразие прототипов наноструктур, отвечающих триггерам JK- типа, можно свести либо к одной - с изменяемым правилом взаимодействия входных переменных, либо к двум - с зеркально симметричным правилом восприятия собственных состояний. При этом следует иметь в виду, что в разных нановентилях уровню "единицы" может отвечать разное значение кодирующей физической величины
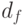 .
. - Методика перехода от конечно-автоматных к комбинационным нановентилям использует два фактора:
- асимметрию в интерпретации собственных состояний взаимодействующих конечно-автоматных наноструктур;
- избирательные ассоциативные восприятия комбинаций значений входных и/или выходных переменных, также зависящие от внутренних состояний.
- "Наносхемотехники" могут ослабить требования к устойчивости и прецизионности библиотечных конечно-автоматных нановентилей-прототипов и особенно их комплексов, если переведут методы и средства формально-логического синтеза схем в базис непрерывноз-начных нейроподобных элементов, модели которых в большей мере адекватны физико-техническим процессам реальных нановентилей, чем переключательные модели двузначных логических элементов.
- В условиях реального синтеза комбинационных нановентилей может оказаться, что логическая простота соединений конечно-автоматных нановентилей не приводит к лучшей устойчивости, и поэтому предпочтение придется отдавать более тесно взаимодействующим субнаноструктурам, в которых практически полностью использована вся мощь "тирании" квантовых связей синтезированного комплекса.
- Роль нанотриггеров D -типа в наносхемотехнике не ограничивается детектированием виртуальных взаимодействий субнаноструктур, так как они могут сыграть еще и роль буферных каскадов, трансформирующих "микроэлектронные потенциалы" в наноэлектронные и наоборот.
- Если объединить все рассмотренные способы и приемы устранения схемотехнической неоднозначности, то получим обобщенную структурно-функциональную схему нановентиля (рис. 7.25).
В основе этой схемы лежит избирательное ассоциативное структурно-параметрическое управление виртуальным и/или материальным взаимодействием составляющих нановентилей конечно-автоматного типа. Избирательность взаимодействия поддерживается соответствующими схемами дешифрации входных и выходных сигналов, а также внутренних состояний, формирующих сигналы обратных связей во всем квантовом комплексе.
Проведенный анализ специфики работы наноэлектронной элементной базы, использующей в своей работе "неквантовую" суперпозицию субнаноструктур конечно-автоматного типа, позволяет заключить:
- Дуализм наноэлектроники является следствием квантового дуализма, и проявляется он в том, что здесь сосуществует два взаимообусловленных, но тем не менее разных вычислительных процесса. Один поддерживается материальными нановентилями и реализуется через логические функции конечно-автоматного типа, а второй поддерживается виртуальными вентилями и реализуется через логические функции комбинационного типа.
- Основная специфика синтеза вычислительных наноструктур состоит в том, что само "сближение" квантовых систем приводит к их трансформации, которая представляет собой иной тип их возбуждения. Такое возбуждение сопровождается как минимум перераспределением массы, заряда и/или энергии в системе в целом, а значит, и изменением преобразований, реализуемых "сближаемыми" компонентами. Поэтому абстрактный синтез детерминированных материальных и виртуальных нановентилей способен отразить только требуемый его итог. Функции реальных элементарных конечных автоматов, участвующих в синтезе, при их рассмотрении вне контекста схемы результирующего взаимодействия необходимо доопределять. 3. (Нано)схемотехника, в которой конечный автомат первичен, а комбинационный автомат вторичен, адекватна оптоэлектронным МКМД-бит-потоковым вычислительным технологиям [130, 138-141] и сохраняет преемственность с кремниевой компиляцией, дополняя ее двумя более низкими уровнями абстрактно-логич еского и физико-технического синтеза. Первый из этих уровней соответствует су бнанометровым взаимодействиям, для описания которых можно использовать нановентили D- типа, а второй уровень соответствует нанометровому взаимодействию, функции которого можно представить различными нанотриггерами JK- типа.
7.6. Особенности нейроподобной схемо-и системотехники
В вычислительной технике исторически первыми "нарушителями" отношения "простой-сложный" были сторонники нейроподобных вычислений [64, 71, 77]. Они исходили из того, что "более сложные" логические функции 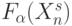 реализуются последовательностью "более простых" преобразований:
реализуются последовательностью "более простых" преобразований:
![(l_{s}(X^{s}_{n},W_{n}) = \sum_{i=1}^{n}{x_i}*{w}_i)\in (h_{j-1},h_{j}]\Rightarrow f_{s} : = b_j,](/sites/default/files/tex_cache/e94e94d1d5135e9e4eb64620af289cb1.png) |
( 7.15) |
которые включают:
- покомпонентную свертку
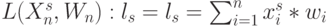 .
.входного вектора
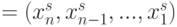
и весового вектора
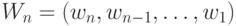 ,
,где
 ,
,  ,
, 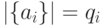 ,
, 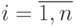 ,
,  ,
,  ;
; - разбиение
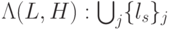 скалярной оси
скалярной оси 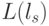 на
на 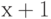 пороговых полуинтервалов
пороговых полуинтервалов ![\{(h _{j-1}, h_j]](/sites/default/files/tex_cache/c6c5cc9aa931391af0b62b4ba084469d.png) , где
, где  - компоненты вектора порогов
- компоненты вектора порогов 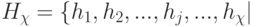 ,
, 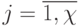 .
. - подстановку
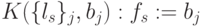 значений реализуемой (дискретной) функции
значений реализуемой (дискретной) функции 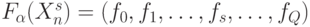 , которая зависит от условия:
, которая зависит от условия: ![l_s\in(h_{j-1}, h]\Rightarrow f_s:=b_j](/sites/default/files/tex_cache/36a41acb57d7a229c3df3cfe63941481.png) ; где
; где  ,
,  ,
, 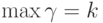 и при минимально пороговой реализации:
и при минимально пороговой реализации: 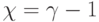 ,
, 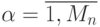 , а
, а 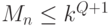 - мощность класса
- мощность класса  -значных функций, реализуемых
-значных функций, реализуемых  -входовым формальным нейроном ( ФН ).
-входовым формальным нейроном ( ФН ).
Вопрос о соотношении "сложности" арифметических и логических выражений в математике и логике не стоит, так как, согласно теореме К. Геделя о полноте [3], любой логической системе можно поставить в соответствие некоторую арифметическую. Поэтому открытым остается только вопрос о стоимостных характеристиках реализации арифметических выражений через логические и наоборот.
Исторически физико-технические процессы цифровой микроэлектроники оказались адекватными переключательным функциям, в результате чего более дешевой здесь оказалась реализация арифметических функций через логические.
С этих позиций отсутствие ощутимых практических успехов в нейро-компьютерных технологиях можно объяснить следующим:
- Нейроподобная системотехника сохраняла традиционную для вычислительной техники декомпозицию на блоки и устройства, используя не многозначный, а двузначный вентильный базис в схемотехнике ФН [68]. При таком подходе фактически выполняется двойной переход от булева базиса к арифметико-комбинаторному и наоборот, так как большинство блоков и устройств вычислительной техники реализует логические функции. Поэтому даже по средневзвешенным (на одну логическую функцию) аппаратным затратам ФН объективно проигрывали универсальным логическим модулям на селекторах-мультиплексорах [223], которые существенно упрощают схемотехнику СБИС и их кремниевую компиляцию.
- Методы и алгоритмы оптимальной декомпозиции заданной функции до операционного базиса ФН [77, 80] значительно уступали по размерности алгоритмам синтеза комбинационных и микропрограммных автоматов [107, 224-225].
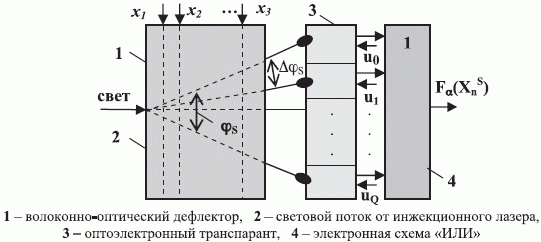
В оптоэлектронном ФН (рис. 7.26 [217]) наиболее аппаратно емкую операцию (свертку входного и весового векторов) выполняет волоконно-оптический дефлектор, и делает это не на схемотехническом, а на физическом уровне работы. В этой схеме угол отклонения луча описывается соотношением
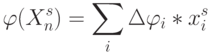
а комбинаторные преобразования (разбиения и подстановки) реализует транспарант с электрически управляемой (сигналами 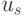 ) "прозрачностью" его элементов.
) "прозрачностью" его элементов.
Тем не менее, и здесь не удалось достичь ощутимых практических успехов из-за высокого (по отношению к микроэлектронным изделиям) энергопотребления и технологических сложностей реализации варьируемых коэффициентов (углов отклонения 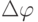 ) в дефлекторе. В результате вся задача функциональной адаптации оптоэлектронного ФН сосредоточилась в его комбинаторных преобразованиях, что резко повысило требования к пространственной избирательности дефлектора и транспаранта до
) в дефлекторе. В результате вся задача функциональной адаптации оптоэлектронного ФН сосредоточилась в его комбинаторных преобразованиях, что резко повысило требования к пространственной избирательности дефлектора и транспаранта до  , чтобы такой ФН, как и селектор-мультиплексор, был полон по отношению к классу булевых функций
, чтобы такой ФН, как и селектор-мультиплексор, был полон по отношению к классу булевых функций  -переменных.
-переменных.
Таким образом, при выборе "элементарного" операционного базиса одной адекватности физических процессов логическим или арифметико-комбинаторным явно недостаточно и требуется оценка конструктивно-технологических и системотехнических последствий, первые из которых предопределяют энергопотребление вычислителей и потенциально достижимый уровень микроминиатюризации (перспективы развития), а вторые представляют, ограничивают или перераспределяют ресурсы управления вычислительным процессом.
Обращает на себя внимание то обстоятельство, что наиболее интенсивно продолжает развиваться системная и прикладная нейроматематика, а модели элементной базы нейрокомпьютеров не претерпели кардинальных изменений с начала 50-х годов этого столетия. Так, в основе большинства моделей ФН лежит (много)пороговая модель, импликативная форма записи которой имеет вид (7.15). В зависимости от структурного алфавита 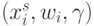 этой модели отличают:
этой модели отличают:
- двузначные ФН с
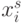 ,
, 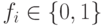 ;
; - многозначные ФН с
 ,
, 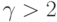 ;
; - непрерывнозначные ФН с
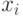 ,
,  ;
; - одно- и многопороговые ФН с
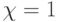 и
и  соответственно;
соответственно; - мажоритарные ФН с
 или
или 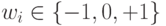 ;
; - с нелинейным входным преобразованием [149]
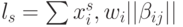 , где матрица
, где матрица 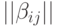 учитывает перекрестные синаптические связи;
учитывает перекрестные синаптические связи; - ассоциативные ФН [13] с
 и т.
и т.
Отличительные черты современных моделей ФН:
- Используют нелинейное внутреннее (пороговое) преобразование свернутого тем или иным способом вектора входных переменных.
- Описывают работу многофункциональных или универсальных (полных по отношению к некоторому классу
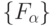 ) комбинационных автоматов, из которых требуемые конечные автоматы получаются за счет смещенных во времени вариаций
) комбинационных автоматов, из которых требуемые конечные автоматы получаются за счет смещенных во времени вариаций 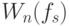 и/или
и/или  .
. - Имеют избыточную систему управления по
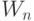 и
и 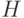 , с помощью кото-рых селектируется требуемая
, с помощью кото-рых селектируется требуемая  .
. - В явном виде не представлены свойственные реальным нейронам фактор временной интеграции (суммации) внешних воздействий и фактор переноса вещества, которые существенно влияют на функционирование реальных нейронов, определяя их структурную адаптацию, и которые пока представлены в биофизических и биохимических моделях.
В 60-х годах прошлого столетия из теории ФН выделилось самостоятельное направление, названное пороговой логикой, в рамках которого решался комплекс проблем оптимальной декомпозиции заданной функции в базисе "элементарных" (много)пороговых функций, реализуемых элементами сети из ФН. При этом сам ФН рассматривался как параметрически адаптируемый элемент с варьируемыми компонентами векторов 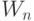 и
и 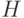 .
.
В 70-х годах прошлого столетия на основе результатов пороговой логики сформировалась самостоятельная теория дискретных многофункциональных модулей, в рамках которой изучались селективные возможности различных преобразований информационных и/или управляющих переменных с учетом схемотехнических особенностей реализации операционного ядра многофункциональных модулей. В результате были исследованы взаимосвязи методов структурной и параметрической адаптации многофункциональных модулей, но остались без внимания вопросы избыточного управления ФН.
Немаловажно также, что сторонники нейроподобных вычислений практически первыми исследовали самые разнообразные топологии сетей, от произвольно коммутируемых Мак-Каллока - Питтса и до многоярусных по типу "каждый с каждым" в персептронах Ф. Розенблата. В этих исследованиях основное внимание уделялось самой топологии связей ФН и считалось, что реальные гальванические или оптические каналы имеют нулевое время задержки. При этом игнорировался тот факт, что в широко разветвленных аксонно-коллатеральных связях реальных нейронов время
распространения возбуждения, как правило, не менее чем на порядок превосходит длительность самого "спайка", а сам процесс его распространения по нейросети в большей мере соответствует FIFO- регистровым, а не гальваническим или оптическим каналам обмена.
Исследования в области нейрокомпьютеров и у нас, и за рубежом пока еще ведутся в заметном отрыве от нанотехнологических исследований, хотя уже появился ряд работ по аппаратурной реализации нейрочи-пов нанометрового диапазона, чего нельзя сказать об инструментальных средствах и математических основах, объединяющих эти классы вычислителей. Сложность проектной и эксплуатационной схемо- и системотехнической проблематики эффективного программно-аппаратного управления вычислительными ресурсами нанометровых компьютеров вытекает из требований к современным опто- и микроэлектронным вычислительным системам (ВС), где бесспорными лидерами являются ВС реального времени ( РВ ), которые в военных и ответственных приложениях должны быть сверхпроизводительными, многоуровневыми, неоднородными, распределенными, динамически реконфигурируемыми, отказоустойчивыми, отказобезопасными, защищенными от несанкционированного доступа и вмешательства в ход вычислительного процесса извне.
Очевидно, что нанометровые вычислители составят конкуренцию (суб)микронным, если удовлетворят этим требованиям, но с более высокими показателями качества, в которые решающий вклад вносят аппаратно-временные затраты на управление потоками инструкций и данных.
В вычислительной технике объектом управления фактически являются не операционные устройства, которые служат средством преобразования информации, а циклически обрабатываемые потоки инструкций и данных, причем цикличность здесь выступает как атрибутивное свойство, без которого невозможно окупить весь спектр затрат на разработку и эксплуатацию ВС.
В традиционных аналоговых вычислителях, работающих по принципу "один поток-оператор - одно операционное устройство", потоки данных могут обрабатываться только в хронологическом порядке. Поэтому конкретная последовательность пространственно фиксированного набора поток-операторов инициализируется по мере распространения потока данных с условным (зависимым от содержимого данных) и/или безусловным (зависимым только от времени) шунтированием операционных устройств, то есть за счет реконфигурации сети коммутации таких вычислителей. При этом смена решаемой задачи требует полной или частичной замены операционных устройств и сети их коммутации, что соответствует структурно-функциональной адаптации всего аналогового вычислителя, а цикличность обработки потоков данных - периодического системного сброса и/или задания начальных условий в каждом специализированном операционном устройстве, что соответствует его параметрич еской адаптации.
В традиционных цифровых вычислителях порядок поступления инструкций и данных на обработку диктует заложенный в программу алгоритм решения задачи и он, как правило, отличается от хронологического, который характерен для предметной области. Поэтому в отличие от аналоговых вычислителей, где допустимы только временные сдвиги между потоками данных, не нарушающие хронологический порядок их следования внутри потока, в цифровых вычислителях изменение порядков "чтения-записи" внутри потоков входных и/или выходных данных можно считать неотъемлемой составляющей любого вычислительного процесса.