| Россия, Москва, МЭИ, 2006 |
Системотехнические аспекты перспективных компьютерных технологий
7.2. Базовая модель алгоритмически ориентированных супрамолекулярных вычислителей
В отличие от КК, которые пока еще "более реалистичны, чем реальны", СМК фактически существуют в течение последних 40-50 лет [191] в виде макросистем измерения кинетики ферментативных реакций с периодом полупревращения менее 10-9 с. В схемо- и системотехническом аспекте основное достоинство СМК состоит в том, что переходные процессы в них происходят с выделением и поглощением энергии и тем не менее они сохраняют на макроуровне целый ряд атрибутивных свойств квантовых систем, что позволяет отрабатывать на их основе архитектурные решения до промышленного освоения нанотехнологий.
Существенно используя [191], рассмотрим ферментативную реакцию множества субстратов  и множества продуктов
и множества продуктов 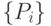 , которые взаимодействуют в строгом порядке благодаря высокой специфичности ферментов
, которые взаимодействуют в строгом порядке благодаря высокой специфичности ферментов 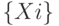 , каждый из которых образует ферментосодержащий комплекс ( ФСК ) с единственным из участвующих в реакции субстратов:
, каждый из которых образует ферментосодержащий комплекс ( ФСК ) с единственным из участвующих в реакции субстратов:
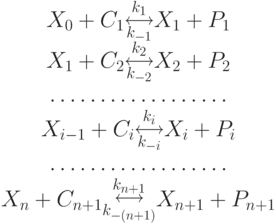 |
( 7.1) |
где 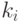 и
и 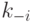 - индивидуальные константы скоростей ассоциации и диссо-циации.
- индивидуальные константы скоростей ассоциации и диссо-циации.
В основе релаксационных методов контроля кинетики таких реакций лежит тот факт, что если на находящуюся в равновесном состоянии систему подать быстрое возмущение какой-либо интенсивной переменной, определяющей положение равновесия, то эта система перейдет в новое положение равновесия в течение определенного, характерного для нее времени  (время релаксации). В качестве интенсивных переменных обычно используют давление, электрическое поле или температуру
(время релаксации). В качестве интенсивных переменных обычно используют давление, электрическое поле или температуру
Если протекающая в системе химическая реакция содержит несколько стадий по типу (7.1), то временная зависимость процесса релаксации определяется спектром временных констант  , каждая из которых соответствует определенной
, каждая из которых соответствует определенной  -й стадии. Такой релаксационный спектр может иметь как дискретное, так и непрерывное распределение около определенного значения времени, но в любом случае возмущение интенсивной переменной должно быть "слабым", чтобы новое положение равновесия не слишком отличалось от исходного. Поэтому при использовании релаксационной измерительной системы в качестве вычислительной, как и в КК, требуется дополнительная фаза восстановления исходного состояния, что гарантирует стабильную зависимость спектра времен релаксации от возмущающей интенсивной переменной, но снижает быстродействие.
-й стадии. Такой релаксационный спектр может иметь как дискретное, так и непрерывное распределение около определенного значения времени, но в любом случае возмущение интенсивной переменной должно быть "слабым", чтобы новое положение равновесия не слишком отличалось от исходного. Поэтому при использовании релаксационной измерительной системы в качестве вычислительной, как и в КК, требуется дополнительная фаза восстановления исходного состояния, что гарантирует стабильную зависимость спектра времен релаксации от возмущающей интенсивной переменной, но снижает быстродействие.
Изменение парциального давления можно реализовать в периодической форме, воспользовавшись ультразвуком. Когда частота возмущений невелика, равновесные концентрации и равновесная степень диссоциации системы  успевают периодически изменяться в фазе с интенсивной переменной
успевают периодически изменяться в фазе с интенсивной переменной  , где
, где 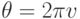 , а
, а 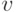 и
и 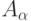 - частота и амплитуда колебаний.
- частота и амплитуда колебаний.
С ростом частоты наблюдаемая степень диссоциации  не успевает точно отслеживать изменения интенсивной переменной и
не успевает точно отслеживать изменения интенсивной переменной и 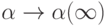 . В этом случае:
. В этом случае:
 |
( 7.2) |
Решение (7.2) показывает, что фактическая степень диссоциации а следует за равновесной  с амплитудой в
с амплитудой в 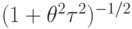 раз меньшей и с разностью фаз
раз меньшей и с разностью фаз 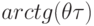 , причем в области частот
, причем в области частот 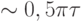 амплитуда колебаний
амплитуда колебаний  .
.
Поэтому в интервале частот, где 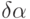 начинает отставать по фазе от изменения давления, обуславливающего изменение
начинает отставать по фазе от изменения давления, обуславливающего изменение  , наблюдается дополнительное поглощение ультразвука с максимумом при
, наблюдается дополнительное поглощение ультразвука с максимумом при 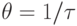 .
.
Характер зависимости скорости химической реакции от электрического поля является полимодальным и определяется валентностью, электрофоретической подвижностью и электрическим зарядом реагентов, а также диэлектрической проницаемостью среды. Поскольку сильные поля приводят к повышению температуры, использовать периодические изменения такой интенсивной переменной невозможно и приходится прибегать к коротким возмущающим импульсам различной длительности.
Создав условия для большого затухания релаксационного сигнала, реакцию на возмущение единичным импульсом можно рассматривать как апериодический процесс, в котором отсутствуют колебания.
Если пропустить через раствор импульс тока высокого напряжения, то температуру раствора можно повысить на 10 oС менее чем за 1 мкс. Это позволяет представить изменение температуры ступенчатой функцией, в которой скачок происходит за время, пренебрежимо малое по сравнению со временем релаксации.
При таких условиях  можно считать постоянной,
можно считать постоянной,  .
.
Для линеаризации выражений, описывающих скорость релаксации в процессах типа (7.1), создаются такие условия, при которых концентрационные переменные каждой стадии можно представить 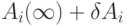 и пренебречь членами более высокого порядка относительно
и пренебречь членами более высокого порядка относительно  . В этом случае система уравнений для скоростей релаксации принимает вид:
. В этом случае система уравнений для скоростей релаксации принимает вид:
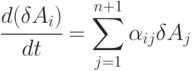 |
( 7.3) |
где 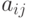 - константы, зависящие от скоростей и равновесных концентраций каждой стадии.
- константы, зависящие от скоростей и равновесных концентраций каждой стадии.
В матричной форме (7.3) можно представить:
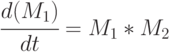 |
( 7.4) |
где: 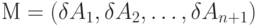 - матрица-столбец, а
- матрица-столбец, а  - матрица коэффициентов
- матрица коэффициентов 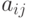 размером
размером  .
.
Решение (7.4) имеет вид:
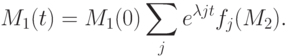 |
( 7.5) |
Соотношение (7.5) можно принять за вычислительную модель процесса измерения времени релаксации системы ферментативных реакций типа (7.1), где 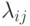 - характеристические числа матрицы
- характеристические числа матрицы  , a
, a
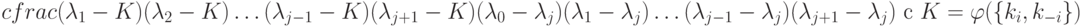
Таким образом, 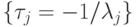 образуют спектр времен релаксации, в котором число временных констант соответствует числу независимых стадий процесса (7.1), но индивидуальные времена релаксации невозможно отнести к конкретной элементарной стадии. Это можно интерпретировать как (макро)проявление на уровне (био)молекулярных систем квантового принципа суперпозиции или как множественность времен [192] для локальных квантовых систем.
образуют спектр времен релаксации, в котором число временных констант соответствует числу независимых стадий процесса (7.1), но индивидуальные времена релаксации невозможно отнести к конкретной элементарной стадии. Это можно интерпретировать как (макро)проявление на уровне (био)молекулярных систем квантового принципа суперпозиции или как множественность времен [192] для локальных квантовых систем.
В качестве примера приведем полученные таким методом соотношения для времен релаксации двухступенчатой реакции типа (7.1) [191]:
![\tau_1 = \cfarc{1}
{k_1[C(\infty)+X_0(\infty)]+k_{-2}[P(\infty)+X_0(\infty)]+k_{-1}+k_2},\\
\tau_2 = \cfarc{k_1[C(\infty)+X_0(\infty)]+k_{-2}[P(\infty)+X_0(\infty)]+k_{-1}+k_2}
{X_0[k_1k_{-2}(x_0(\infty)+P(\infty)+C(\infty))+k_1k_2+k_{-1}k_{-2}]},](/sites/default/files/tex_cache/c0116a48aee33e8fe85dc8e191941fb2.png)
Из этих соотношений видно, что релаксационную схему измерения кинетики ферментативных реакций типа (7.1) можно использовать двояко в зависимости от того, какие из составляющих аргументов являются параметрами, а какие - переменными.
Если зафиксировать концентрации 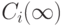 ,
,  , что соответствует флуктуациям реакции около положений равновесия с близкими концентрациями, то релаксационная схема пригодна для "вычисления" зависимостей
, что соответствует флуктуациям реакции около положений равновесия с близкими концентрациями, то релаксационная схема пригодна для "вычисления" зависимостей 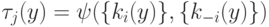 , что соответствует использованию "слабой" интенсивной переменной
, что соответствует использованию "слабой" интенсивной переменной  в качестве информационной.
в качестве информационной.
Если ферментативную реакцию последовательно переводить с помощью "сильной" интенсивной переменной  в равновесные состояния с существенно отличными концентрациями, то "вычисление"
в равновесные состояния с существенно отличными концентрациями, то "вычисление" 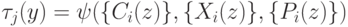 можно рассматривать как "релаксационную идентификацию" достигнутого состояния. Такая "идентификация" осуществляется с помощью другой более "слабой" переменной
можно рассматривать как "релаксационную идентификацию" достигнутого состояния. Такая "идентификация" осуществляется с помощью другой более "слабой" переменной  , влияющей стандартным образом на
, влияющей стандартным образом на 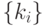 и
и 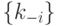 , но не на изменение равновесных концентраций.
, но не на изменение равновесных концентраций.
При этом "сильные" и "слабые" переменные, вообще говоря, должны быть различной физической модальности, например давление и электрическое поле. При однотипной модальности эти переменные можно разделить частотно: "сильная" информационная переменная должна быть низкочастотной, а "слабая идентификационная" - высокочастотной.
С вычислительных позиций интерес представляют многостадийные циклические ферментативные реакции типа (7.1) с кратностью и/или коэффициентом вложенности циклов большим или равным единице, где в конечном счете 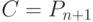 , что соответствует устойчивой реализации зависимостей
, что соответствует устойчивой реализации зависимостей 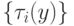 или
или 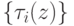 .
.
Из базовой модели видно, что в ФСК- вычислителях, повторяющих схему измерения кинетики ферментативных реакций, кроме управляющих и информационных переменных в явном виде присутствуют глобальные идентификационные переменные (ультразвук, температура и т. п.), с помощью которых определяются либо конечные состояния системы, либо ее переходные характеристики.
В традиционной цифровой опто- и микроэлектронике идентификационные переменные неявно присутствуют в каждом активном элементе (вентиле) в виде пороговых значений "нуля" и "единицы", которые представляют собой их физико-технические характеристики и являются жесткими и распределенными по всем вентилям СБИС или УБИС.
Кроме линейных цепных схем типа (7.1) ферментативные реакции могут протекать по древообразным схемам, в которых по крайней мере некоторые стадии выполняются по одной из возможных ветвей (бифуркаций). В этом случае кинетика ферментативных реакций является нелинейной и она исследуется в рамках термодинамической теории необратимых стационарных процессов, находящихся вдали от равновесного состояния и способных к образованию (самоорганизации) диссипатив-ных структур [33].
В реакциях, катализируемых ферментами, скорость в 1013-1015 раз выше, чем у некатализируемых, но концентрация реагентов в 10-3-10-6 раз меньше 1 М (1 М - один моль, то есть концентрация, которая обычно используется в некатализируемых реакциях). В таких условиях вероятность взаимодействия двух субстратов и одного фермента примерно в 108-1011 раз меньше, поскольку концентрация ферментов обычно не превышает 10-5 М. Тем не менее в ферментативных реакциях вероятность образования продукта гораздо выше, чем в неферментативных, а более высокая скорость и эффективность взаимодействия объясняется двумя эффектами: сближением, которое наблюдается и в обычных каталитических реакциях, и ориентацией, которая присуща, по всей видимости, только ферментативным реакциям, что делает их сходными с квантовыми системами.
Специфичность ферментов определяет выбор субстратов и тот биохимический путь в (7.1), по которому будет идти превращение этих субстратов в продукт. Специфичность проявляется как в выборе субстратов, с которыми фермент образует ФСК (специфичность по входу), так и в характере продуктов, образующихся из ФСК (специфичность по выходу).
Типы связей, обуславливающие специфическое взаимодействие фермента и субстрата, являются полимодальными и покрывают весь спектр от "сильных" ковалентных до "слабых" ионных. Однако вне зависимости от типа ассоциации силы взаимодействия возникают только в ограниченной области фермента, составляющей 2-5 % от общего числа аминокислотных
остатков в его молекуле. Отсюда, специфичность фермента определяется "правильным" расположением по отношению к той связи, которая образуется или разрывается при образовании ФСК, а саму ферментативную реакцию можно рассматривать как масштабированную в 10-8-10-11 раз микромодель неферментативной (каталитической или некаталитической) реакции.
Таким образом, в ФСК- вычислителях сохраняются следующие атрибутивные свойства квантовых систем:
- любая управляющая, информационная или идентификационная (ультразвуковая, электрическая, тепловая и т. п.) переменная изменяет состояние и/или динамику ферментативной реакции, что в квантовых системах соответствует взаимодействию по типу "каждый с каждым";
- переходные процессы в ферментативных реакциях характеризуются спектром аналитических зависимостей времен релаксации, которые невозможно отнести к какой-либо одной стадии, что соответствует принципу суперпозиции стационарных состояний квантовых систем;
- ферментативные механизмы "узнавания", определяющие специфичность ФСК, являются макромолекулярным аналогом пространственно-временного распределения потенциальных барьеров, задающих структурно-функциональные схемы SET-электронных и квантовых вычислителей;
- узловой механизм ФСК-селекции использует ориентацию макромолекул, которая в интегральном виде отражает полимодальные взаимодействия, определяемые пространственно-временным распределением механических, электромагнитных и спиновых моментов в атомарных и молекулярных структурах.

