| Россия, Москва, МЭИ, 2006 |
Системотехнические аспекты перспективных компьютерных технологий
7.5. Особенности нанометровой схемотехники
Нанокластеры являются достаточно крупными атомарными и молекулярными образованиями, которые в зависимости от длин свободного пробега [95] могут вести себя и как макросистемы, и как квантовые системы. Поэтому в нанометровой схемотехнике необходимо по максимуму использовать физические возможности макросистем, стабильность которых поддерживается квантовыми взаимодействиями субнаноструктур. С этих позиций видно, что успехи наноэлектроники могут привести к получению наноструктур с устойчивыми когерентными взаимодействиями, удовлетворяющими требованиям реализации либо сугубо квантовых вентилей, либо классических булевых вентилей (см. рис. 7.1). В первом случае нанокомпиляторы будут представлять задачу пользователя в одном из "квантовых" операторов: Паули, Адамара, Уолша - Адамара и т. п. Во втором случае сохранится классическое булево представление задачи пользователя на физическом уровне ее реализации (см. рис. 6.1).
Отсюда, необходимо проанализировать влияние особенностей работы нанометровых булевых вентилей на наносхемотехнику, в рамках которой необходимо будет обеспечить устойчивое взаимодействие порядка 106-1010 вентилей.
Работа активных элементов традиционной цифровой опто- и микроэлектроники базируется на переходных процессах между двумя статическими состояниями, поддерживаемыми физико-техническими параметрами этих элементов. В активных элементах нанометрового диапазона по объективным причинам можно использовать переходные процессы между допустимыми парами стационарных состояний, из которых только одно является устойчивым, так как отвечает требованию минимума энергии. Остальные
состояния являются возбужденными и могут сохраняться в течение ограниченного интервала времени: 0,1-10 сек - для метастабильных состояний атомов или молекул и не более 10-8 сек в противном случае.
Динамический диапазон изменения энергии в переходных процессах атомов или молекул, вообще говоря, ограничен энергией ионизации, а структура допустимых квантовых переходов задается строгими или приближенными правилами отбора, которые вытекают из физических законов сохранения энергии, импульса, момента импульса, электрического заряда и т. д.
При этом каждому закону сохранения соответствует специфическая симметричность полимодальных преобразований:
- закону сохранения полного момента импульса и его проекций - сферическая и аксональная симметрия соответственно;
- закону сохранения четности - инверсии (отражения в центре симметрии) вида
 ,
,  ,
,  , которые запрещают определенные квантовые переходы, обуславливающие электрическое дипольное излучение и т. п.
, которые запрещают определенные квантовые переходы, обуславливающие электрическое дипольное излучение и т. п.
Приближенные правила отбора отличаются от строгих тем, что задают структуру запрещенных переходов с малой, но не равной нулю вероятностью.
С формально-логических позиций такое поведение активных нано-метровых элементов описывается вероятностными автоматами, переходные процессы в которых определяются свойствами симметрии базовой квантовой системой, внешними воздействиями и текущим состоянием, требующим, вообще говоря, регенерации на интервалах времени, превышающих его "время жизни".
Таким образом, в нанометровой схемотехнике:
- инвертируется отношение между комбинационными и конечными автоматами, первые из которых в традиционной опто- и микроэлектронике считаются "более простыми" и служат элементами вторых, "более сложных";
- структура пространства состояний и возможных переходов конечных автоматов задается не схемной композицией комбинационного автомата и элементов памяти, как это имеет место в традиционной вычислительной технике [220], а физическими законами, вытекающими из свойств симметрии атомарных и молекулярных структур, служащих рабочим телом нанометровых вычислителей;
- спонтанные излучения (поглощения) атомарных и молекулярных структур носят атрибутивный характер для субнанометровых взаимодействий и требуют введения в абстрактно-логическую теорию конечных автоматов вероятностных состояний, а не только вероятностных переходов [221], вследствие чего в них остается детерминированным только входной и выходной алфавит;
- исходный квантовый субстрат изменяет свои структурно-функциональные свойства в процессе синтеза наноструктур. В результате только вероятностные конечные автоматы с переменной структурно-функциональной схемой, зависящей от условий взаимодействия с другими автоматами, можно рассматривать в качестве адекватных формально-логических моделей квантовых систем.
Признание этого факта влечет за собой достаточно глубокие схемотехнические последствия в области вычислительной техники нанометро-вого диапазона.
Во-первых, он изменяет на противоположное принятое в современной опто- и (микро)электронике отношение "простой-сложный" между автоматами без памяти (в дальнейшем комбинационные вентили) и автоматами с памятью (в дальнейшем конечно-автоматные вентили), а также роль и место виртуальных вентилей типа "монтажное ИЛИ", уравнивая в правах два типа дуальных взаимодействий между наноструктурами: "материальные", которые связаны с перераспределением, выделением или поглощением заряда, массы и/или энергии, и "виртуальные", которые связаны с суперпозицией электромагнитных полей, создаваемых нанокластерами.
Во-вторых, он фактически приводит к порочному кругу, в котором апостериорные знания о синтезированной эмпирическим путем наноструктуре мало что говорят об исходном субстрате и тем более не дают никакой информации о порядке взаимодействия исходных компонент в процессе синтеза наноструктуры. В свою очередь, априорные знания компонент не раскрывают свойств результирующей нанострутуры и мало говорят о порядке их взаимодействия, которым необходимо воспользоваться для синтеза нановентилей с заранее заданными структурно-функциональными свойствами.
При строгом подходе микроэлектронный транзистор также необходимо рассматривать как конечный автомат [222], подавление негативных реакций которого требует определенных технологических усилий, компенсирующих влияние обратных связей, которые образуются из-за паразитных емкостей схемы. Но в случае (микро)электроники основные свойства транзистора остаются практически неизменными или, по крайней мере, предсказуемыми как при его (правильном) включении в схему, так и вне этой схемы.
Поэтому современные трудности промышленного освоения нанотех-нологий можно объяснить, в частности, тем обстоятельством, что их создатели стремятся воплотить на качественно новом физико-техническом уровне организации вычислений традиционные схемотехнические решения, основанные на детерминированных комбинационных вентилях, которые сохраняют свои схемотехнические свойства как внутри, так и
вне схем их (правильного) включения. Такой подход направлен на обеспечение полной преемственности проектных наработок, накопленных в микроэлектронной схемо- и системотехнике. Но при этом перед физиками встает целый ряд трудноразрешимых проблем, которые связаны не только с декогерентизацией, ограничивающей время жизни "нановычис-лителя", но и с полным подавлением "тирании соединений" и паразитных взаимодействий как между наноструктурами, так и между составляющими их субнаноструктурами.
Чтобы ослабить остроту физико-технических проблем построения устойчивых базисных нановентилей, можно отказаться от схемотехнических "постулатов" микроэлектроники и взять в качестве неделимой единицы схемотехнического проекта конечный, а не комбинационный автомат (автомат без памяти). В этом случае системотехническую основу перспективных нанокомпьютеров может составить МКМД-бит-потоковая вычислительная технология [138-141], в которой процессы передачи данных по FIFO- регистровым, а значит, конечно-автоматным каналам являются первичными и совмещены в пространстве и во времени с процессами их обработки в последовательной конвейерной арифметике, которая является вторичной.
На современном этапе сближения позиций физиков и "наносхемо-техников" задачу поиска адекватного формально-логического описания наноструктур можно временно упростить и считать, что исходный квантовый субстрат ведет себя как детерминированный конечный автомат, в котором осуществляются те и только те переходные процессы, которые требуются, и происходят они с "вероятностью единица". Такое допущение уводит нас от реальных условий синтеза нановентилей. Тем не менее, на его основе можно построить модели, которые дают представление о требуемых схемах объединения в один комбинационный нановен-тиль исходных наноструктур, обладающих четко выраженными конечно-автоматными свойствами. При этом от наноструктур-прототипов требуется, чтобы после такого объединения они либо практически не изменяли свои функции, либо эти изменения должны соответствовать функциональному назначению окончательного квантового субстрата в составе синтезированного нановентиля.
Раскроем особенности (нано)схемотехники, в которой элементарные конечные автоматы считаются первичными и реализуются за счет устойчивого обмена зарядами, массой и/или энергией в квантовых системах, а виртуальные комбинационные вентили типа "монтажное ИЛИ", "монтажная НЕРАВНОЗНАЧНОСТЬ" и т. п. считаются вторичными и реализуются за счет устойчивых суперпозиций электромагнитных полей, создаваемых элементарными наноструктурами. При этом считается, что используемые нанокластеры ведут себя как макросистемы, в которых "неквантовая" суперпозиция представляет собой взвешенную сумму взаимодействующих электромагнитных полей.
В такой постановке задачи от "наносхемотехников" прежде всего требуется разработать формально-логические методы и приемы устранения неоднозначных реакций конечных автоматов, входящих в каждый нановентиль как атрибут, за счет фиксации функционально значимых взаимодействий электромагнитных полей как между субнаноструктурами одного нановентиля, так и между самими нановентилями, сохранившими свои конечно-автоматные передаточные функции.
Под неоднозначной реакцией детерминированного конечного автомата понимается зависимость его выхода от внутреннего состояния, в результате чего на одно и то же входное воздействие такой автомат может отреагировать то "нулем", то "единицей", что рассматривается как неправильная работа комбинационного автомата.
Двойственная природа квантового субстрата позволяет заложить преобразуемую информацию как в вещество, так и в электромагнитное поле. Это приводит к следующей классификации нановентилей по признаку носителя входной и выходной информации: с материальными входами и материальным выходом, с виртуальными входами и виртуальным выходом, с материальными входами и виртуальным выходом, с виртуальными входами и материальным выходом.
В (микро)электронике имеется аналог только вентилей второй группы, так как общая схема работы любого транзистора по этому признаку классификации имеет вид: "поле - вещество - поле".
Таким образом, главной целью исследований является раскрытие схем устойчивого взаимодействия материальных конечно-автоматных нановетилей-прототипов, которые трансформируют весь комплекс в комбинационный нановентиль с доступными пользователю входами-выходами. При этом сами квантовые взаимодействия представляются "внутренними" виртуальными вентилями комбинационного типа, входы и выходы которых доступны производителю и недоступны пользователю нановентиля. Фактически ставится задача не борьбы с "тиранией связей" и паразитными взаимодействиями в квантовых системах, а их конструктивного использования при устранении неоднозначных реакций простейших конечно-автоматных нановетилей, образующих комбинационный нановентиль.
Вне рамок рассмотрения пока остаются такие важные вопросы наносхемотехники, как:
- направленное изменение структурно-функциональных свойств исходного квантового субстрата, происходящее в результате такого объединения конечно-автоматных нановетилей-прототипов;
- создание распределенных источников и/или аккумуляторов энергии в квантовых системах и средств синхронизации работы ее компонент.
Предпосылки. Схемотехнические методы и средства устранения неоднозначных физико-технических реакций используются в (микро)схемо-технике как минимум в двух случаях: при переходе от RS- к D- триггерам и при переходе от RS- к JK- триггерам.
Если RS- триггер (рис. 7.10) выполнен на вентилях "И - НЕ", то непрогнозируемая неоднозначная реакция в нем возникает под воздействием комбинации входных переменных R = S = 1 (табл. 7.2), которая вызывает "гонки" в цепях обратной связи.
Как раз наличие "гонок" на физико-техническом уровне организации работы RS- триггера и предопределяет тот факт, что при одном и том же входном воздействии R = S = 1 он непрогнозируемым образом реагирует переходом то в "нулевое", то в "единичное" состояние. (Здесь и далее используются традиционные для вычислительной техники обозначения состояний триггера в текущий ( 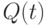 ) и предшествующий (
) и предшествующий (  ) моменты времени, а также сигналов установки "единичного" (
) моменты времени, а также сигналов установки "единичного" (  ) и "нулевого" (
) и "нулевого" (  ) состояний.)
) состояний.)
| Базис И - НЕ | RS | JK | |
|---|---|---|---|
 |
 |
 |
 |
| 0 | 0 | 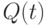 |
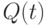 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | l | l |
| 1 | 1 | * | 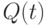 |
В (микро)электронике такая "физико-техническая неоднозначность" устраняется с привлечением ресурсов схемотехнического уровня организации вычислений:
- в D-триггере (рис. 7.11) - за счет обеспечения такого взаимодействия на его входах
 ;
;  , которое исключает
появление комбинации теперь уже промежуточных сигналов R = S = 1, приводящих к неоднозначной реакции в RS-триггере;
, которое исключает
появление комбинации теперь уже промежуточных сигналов R = S = 1, приводящих к неоднозначной реакции в RS-триггере;
- в классическом двухполупериодном JK-триггере (рис. 7.12) - за счет введения "глобальных" обратных связей, которые изменяют "восприятие" "неоднозначной" комбинации значений входных переменных
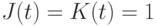 в зависимости от внутреннего состояния:
в зависимости от внутреннего состояния:![[S(t),R(t)]:=
\begin{cases}
J(t) = 1,K(t) = 0, & \text{если } Q(t-1) = 0, \\
J(t) = 0,K(t) = 1, & \text{если } Q(t-1) = 1.
\end{cases}](/sites/default/files/tex_cache/dddd74a96e972378a65906070980e457.png)
Здесь сдвоенным символом
 обозначен оператор присваивания.
обозначен оператор присваивания.
Реализуемое JK- триггером преобразование имеет вид  (табл. 7.3), где ассоциативное [46] взаимодействие предыдущего внутреннего состояния с входными переменными вызывает инверсию последующего внутреннего состояния при появлении на его входах той комбинации переменных, которая приводит к неоднозначной физико-технической реакции RS- триггера.
(табл. 7.3), где ассоциативное [46] взаимодействие предыдущего внутреннего состояния с входными переменными вызывает инверсию последующего внутреннего состояния при появлении на его входах той комбинации переменных, которая приводит к неоднозначной физико-технической реакции RS- триггера.
Первый схемотехнический способ позволяет полностью устранить неоднозначность реакции RS- триггера, но он обедняет отображение "вход-выход" до тавтологии, и поэтому D- триггеры способны выполнить только коммутационные или интерфейсные функции, в которых выход и должен быть равен входу с задержкой на один такт:  .
.
В классическом JK -триггере отображение "вход-выход" богаче:
 |
( 7.10) |
но в нем устранена только физико-техническая неоднозначность и не устранена неоднозначность схемотехнического уровня организации вычислений. Избавиться от этого типа неоднозначности не удается ни одним из четырех возможных способов задания ассоциативных обратных связей, которые приводят к реализации функций табл. 7.3. Во всех перечисленных случаях любой из JK- триггеров продолжает вести себя как конечный автомат, реакция которого продолжает зависеть не только от внешних сигналов, но и от внутреннего состояния. В результате любой из JK- триггеров, реализующий функции табл. 7.3, сохраняет свои конечно-автоматные свойства и продолжает реагировать неоднозначно в указанном выше смысле.
| Базис И НЕ | RS |  |
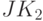 |
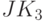 |
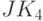 |
||
|---|---|---|---|---|---|---|---|
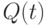 |
 |
 |
 |
 |
 |
 |
 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | l | 1 |
| 0 | 1 | 1 | * | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | l | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | * | 0 | 1 | 0 | 1 |
 |
0 | 0 | 1 | 1 | |||
 |
0 | 1 | 0 | 1 | |||
Из приведенных данных следует: если физико-техническая неоднозначность носит случайный и непрогнозируемый характер, то схемотехническая неоднозначность в детерминированных конечных автоматах прогнозируема и проявляется согласно определенным правилам.
Таким образом, в (микро)схемотехнике устранение неоднозначных выходных физико-технических реакций простейших конечных автоматов осуществляется либо введением функциональных связей между входными переменными, которые исключают появление "неоднозначной" их комбинации, либо введением ассоциативных связей между входными и внутренними переменными конечных автоматов, которые изменяют восприятие "неоднозначной" комбинации значений входных переменных. При этом исходный (микро)схемотехнический "субстрат" в виде RS- триггера сохраняет свою неоднозначную физико-техническую при-
роду, но этот тип триггеров используется в микроэлектронике только при синтезе конечных, а не комбинационных автоматов.
Указанные в табл. 7.3 и не применяемые в (микро)схемотехнике способы устранения физико-технической неоднозначности RS- триггера сводятся к следующему:
- При реализации JK- триггером функции
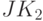 комбинация значений входных переменных
комбинация значений входных переменных 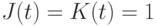 вызывает установку триггера в "единичное" состояние и поэтому ее можно считать эквивалентной комбинации
вызывает установку триггера в "единичное" состояние и поэтому ее можно считать эквивалентной комбинации  ,
,  ;
; - При реализации JK -триггером функции
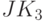 та же комбинация значений входных переменных вызывает установку триггера в "нулевое" состояние и поэтому ее можно считать эквивалентной комбинации
та же комбинация значений входных переменных вызывает установку триггера в "нулевое" состояние и поэтому ее можно считать эквивалентной комбинации  ,
,  ;
; - При реализации JK- триггером функции
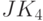 та же комбинация значений входных переменных вызывает сохранение предыдущего состояния и поэтому ее можно считать эквивалентной комбинации
та же комбинация значений входных переменных вызывает сохранение предыдущего состояния и поэтому ее можно считать эквивалентной комбинации  .
.
Синтезируем обобщенный JK- триггер (рис. 7.13), в котором благодаря функциональным связям между входными переменными можно варьировать правилом восприятия комбинации значений входных переменных 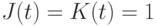 , назначая с помощью управляющих переменных
, назначая с помощью управляющих переменных  конкретный вариант реализуемого отображения согласно правилам табл. 7.3.
конкретный вариант реализуемого отображения согласно правилам табл. 7.3.
Применим схемотехнические приемы (микро)электроники, но теперь уже для устранения схемотехнической неоднозначности выходной реакции обобщенного JK- триггера, который настроен, к примеру, на реализацию функции 

В этом случае проще всего добиться однозначной выходной реакции JK- триггера вида ![F(J(t+1), K(t+1)] = J(t)*\overline{K(t)}](/sites/default/files/tex_cache/66421377bf19ba384f65e04013263b5c.png) ,
которая не зависит от его внутреннего состояния и к тому же обладает базисным свойством в классе булевых функций.
Такую однозначную реакцию можно получить (рис. 7.14 и табл. 7.4) благодаря комплексу мер, в котором используется как функциональная связь между входными переменными, так и специфическая обратная связь, изменяющая восприятие комбинации
,
которая не зависит от его внутреннего состояния и к тому же обладает базисным свойством в классе булевых функций.
Такую однозначную реакцию можно получить (рис. 7.14 и табл. 7.4) благодаря комплексу мер, в котором используется как функциональная связь между входными переменными, так и специфическая обратная связь, изменяющая восприятие комбинации 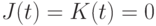 при
при 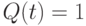 . Это приводит к тому, что указанная комбинация становится эквивалентной комбинации
. Это приводит к тому, что указанная комбинация становится эквивалентной комбинации  ,
,  , но только при "единичном" состоянии этого JK- триггера.
, но только при "единичном" состоянии этого JK- триггера.
| Базис И - НЕ | RS | 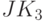 |
||
|---|---|---|---|---|
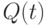 |
 |
 |
 |
 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | * | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | * | 0 |
Такое комплексное, но, тем не менее, достаточно простое для (микро) электроники схемотехническое решение вступает в противоречие с условиями синтеза схем в наноэлектронике, так как оно базируется на дополнительных комбинационных вентилях. В наноэлектронике субнаноструктуры также необходимо считать квантовыми объектами более низкого уровня иерархии, и поэтому их надо описывать "конечно-автоматными" функциями, а не функциями дополнительных комбинационных вентилей рисунков 7.11-7.14.
Отсюда следует, что физик от таких схем может получить только минимальную систему эквивалентных логических преобразований (см. табл. 7.2-7.4). Но воплотить ее он должен на субнанометровом уровне, используя композицию нановентилей конечно-автоматного типа или, что одно и то же, осуществляя инструктированный синтез элементарных наноструктур на основе реализуемых ими и заранее заданных "комбинационных" функций.
При этом необходимо иметь в виду, что физик оперирует комплексом преобразований, которые отражают реальные процессы как перераспределения (переноса) в пространстве и/или во времени массы, энергии, заряда и т. п., так и взаимодействия электромагнитных полей, создаваемых (суб) наноструктурами. Операционный базис этих преобразований образуют арифметические операции, которым только при определенных условиях можно поставить в однозначное соответствие непрерывнозначные или многозначные логические операции. В свою очередь, непрерывнознач-ные или многозначные логические операции только при определенных условиях можно трансформировать в двузначные логические операции.
Поэтому эмпирический синтез элементарных наноструктур, функционально эквивалентных автоматам рисунков 7.11-7.14, можно считать большой творческой удачей физика. Но такой успех еще должен быть развит "наносхемотехником" и "нанотехнологом" до инструктированного синтеза наносхем по заранее известным распределениям в пространстве и во времени "конечно-автоматных" и "комбинационных" функций, поддерживающих вычислительный процесс.






