Символьные вычисления

5.3.2. Ряды, суммы и произведения

Произвольная функция f[var] может быть разложена в степенной ряд в окрестности точки var0 до члена порядка (var-var0)^n при помощи функции Series[f[var],{var,var0,n}]. Слагаемое O[var-var0]^(n+1) в полученном выражении указывает на то, что следующий член ряда будет иметь порядок (n+1). См. соответствующий пример In[1] На рис. 5.16.

Помимо возможности создавать ряды Тейлора функция Series позволяет генерировать ряды, содержащие рациональные и отрицательные степени (пример In[2] на рис. 5.16), а также раскладывать функции в окрестностях бесконечно удалённой точки (пример In[3], аналогичный примеру из книги А.Н. Прокопени и А.В. Чичурина [5, с. 37]).

Иногда Mathematica не может представить ту или иную функцию в виде степенного ряда в окрестностях некоторой точки. Причин тому может быть масса: одна из них, например, сингулярность в этой точке (А. Н. Прокопеня и А. В. Чичурин [5, с. 37]). В этом случае вычисления не производятся, выдаётся предупреждающее сообщение, а в качестве результата возвращается введённое выражение — пример In[4] на рис. 5.16.

Одна из функций, которую нельзя представить в виде ряда — логарифмическая функция. Однако при попытке разложить содержащие её выражения возле нуля или бесконечно удалённой точки ошибки Mathematica не выдаёт: выражение исправно раскладывается в ряд, при этом в окончательном результате логарифм сохраняется в исходном виде (А. Н. Прокопеня и А. В. Чичурин [5, с. 37–38]) — пример In[5] на рис. 5.16.

Разложение в ряд есть некоторая аппроксимация функций, и слагаемое вида O[var-var0]^n является атрибутом этой аппроксимации, поэтому добавление выражения вида O[var]^n к сумме произвольных функций преобразует всю сумму в степенной ряд (А. Н. Прокопеня и А. В. Чичурин [5, с. 38]). Количество слагаемых в сумме не имеет значения: оно может быть и очень большим, и равным нулю. Пример In[6] на рис. 5.16 демонстрирует преобразование некоторого выражения в степенной ряд прибавлением к нему O[x]^6.

Обратную операцию, преобразование степенного ряда ser в обычную сумму, можно при помощи функции Normal[ser], которая отбрасывает остаточный член O[var-var0]^n и конвертирует ряд в многочлен — пример In[7] на рис. 5.16.

Узнать, является ли выражение степенным рядом, можно при помощи хорошо известной нам функции Head. Если выражение expr является степенным рядом, то Head[expr] возвращает SeriesData. В примере In[8] на рис. 5.16 мы применяем Head к полученным в Out[6] и Out[7] выражениям и убеждаемся в том, что первое из них является степенным рядом, а второе — нет.

Mathematica позволяет разлагать выражение в степенной ряд по нескольким переменным. Для этого используется та же функция Series, заданная в виде функции Series[f[var],{var1,var10,nvar1},{var2,var20,nvar2},...]. Эта операция эквивалентна последовательному разложению функции f[var1,var2,...] по переменным var1,var2,... в том порядке, в котором они указаны в функции Series — пример In[9] на рис. 5.16.

увеличить изображение
Рис. 5.16. Разложение функции в степенной ряд

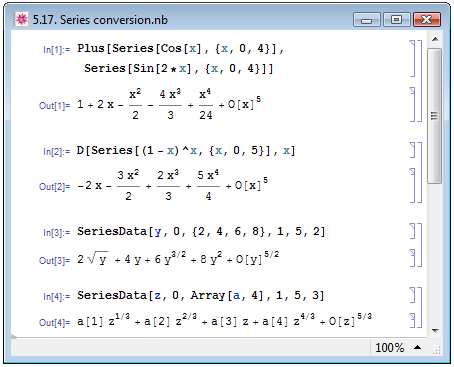
Поскольку степенные ряды содержат обыкновенные математические выражения, с ними можно проделывать обычные математические операции: складывать, перемножать, дифференцировать, интегрировать, возводить в степень и т.д., при этом, в результате образуются новые степенные ряды (Е. М. Воробьёв [1, с. 54] и А. Н. Прокопеня и А. В. Чичурин [5, с. 38] — примеры In[1] и In[2] на рис. 5.17.

Результатом выполнения функции Series является выражение Mathematica, во внутренней форме имеющее заголовок SeriesData. Е. М. Воробьёв [1, с. 55] описывает это выражение следующим образом: "Вычисленное выражение SeriesData[x,x0, {a0,a1,...},nmin,nmax,den] представляет отрезок степенного ряда по переменной x в окрестности точки x0. Величины a0,a1,... есть коэффициенты ряда. Разность x-x0 входит в ряд в степенях nmin/den, (nmin+1)/den,..., nmax/den". При помощи этой функции можно задавать ряд с заданными коэффициентами и степенями выражений при коэффициентах (пример In[3] на рис. 5.17), при этом неопределённые символьные коэффициенты можно задавать при помощи уже известных нам функций Table и Array (пример In[4]).

Подробней о разложении функций в степенной ряд см. книги Е. М. Воробьёва [1, с. 53–55] и А. Н. Прокопени и А. В. Чичурина [5, с. 36–40].

Рис. 5.17. Преобразования рядов и непосредственное задание рядов во внутренней форме

В предыдущем пункте мы познакомились с функциями интегрирования, используемыми при описании непрерывных систем. Для дискретных систем используется функция суммирования.

Сумма в символьной форме вычисляется в Mathematica при помощи функции Sum[expr,int]; количество слагаемых в сумме может быть как конечным, так и бесконечным. Вообще второй аргумент int, задающий интервал изменения переменной, по которой производится суммирование, может быть задан в нескольких формах (А. Н. Прокопеня и А. В. Чичурин [5, с. 41]):

• {i,n} — i изменяется на отрезке от 1 до n с шагом 1;
• {i,imin,imax} — i изменяется на отрезке от imin до imax с шагом 1;
• {i,imin,imax,d} — i изменяется на отрезке от imin до imax с шагом d.

Mathematica стремится выразить любую функцию в виде степенного ряда.

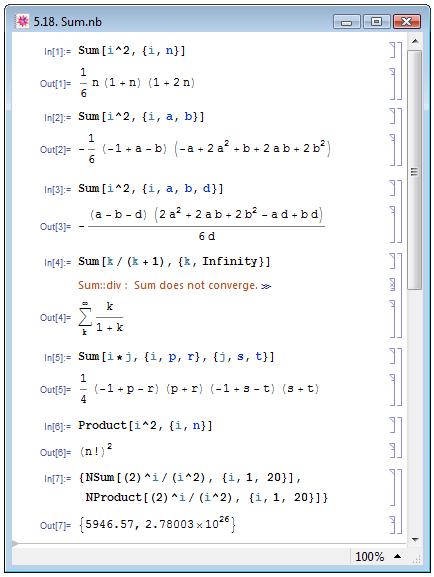
На рис. 5.18 представлены примеры In[1], In[2] и In[3] вычисления суммы при помощи указанных выше выражений.

Если найти результат суммирования в символьной форме не удаётся, Mathematica возвращает сумму невычисленной — In[4] на рис. 5.18.

Mathematica также позволяет вычислить сумму по нескольким индексам i,j,..., для чего необходимо задать функцию в виде Sum[f,{i,imin,imax},{j,jmin,jmax},...] (пример In[5] на рис. 5.18). В заданном формате предполагается, что сумма по i является внешней, поэтому пределы изменения могут зависеть от i, и т.д.

Mathematica также позволяет вычислять произведение выражений в символьном виде, для чего используется функция Product[expr,int], причём правила задания интервала варьирования переменной такие же, как и для такового при суммировании (пример In[6] на рис. 5.18).

По аналогии с интегрированием суммирование и нахождение произведения также могут быть осуществлены численно: при этом результат вычисления будет приближённым (вещественным). Предназначенные для этого функции — NSum и NProduct — примеры In[7] на рис. 5.18.

Подробней о функциях нахождения сумм и произведений см. книгу А. Н. Прокопени и А. В. Чичурина [5, с. 41–43].

Рис. 5.18. Вычисление сумм и произведений