| Россия, Новосибирск, НГПУ, 1994 |
Классы данных в Mathematica
Цель лекции: познакомиться с синтаксисом языка Mathematica, основными типами данных и принципами работы с ними.
2.0. Введение
Как отмечает Е. М. Воробьёв в книге [1, с. 15], в основе работы Mathematica лежат два фундаментальных понятия — выражение и вычисление. Понятие выражениям дают А.Н. Прокопеня и А.В. Чичурин [5, с. 76]: "Любые данные, вводимые пользователем в секции, имеющей тип Input, и предназначенные для обработки ядром, Математика рассматривает как выражения (от слова expression). Простейшими являются так называемые атомарные выражения, т.е. числа, символы и строки".
Выражения, отличные от атомарных, называют сложными.
В общем случае Mathematica оперирует выражениями, относящимися к трём классами данных (Е. М. Воробьёв [2, с. 158]). Это
- численные данные (или числа);
- символьные данные (символы, тексты, формулы);
- списки (массивы данных).
Познакомимся с каждым классом данных в Mathematica. Формат изложения и основные определения позаимствуем в книге В. П. Дьяконова [2].
2.1. Численные данные
Mathematica использует четыре типа чисел: целые, рациональные, вещественные и комплексные, — причём все они относятся к атомарным выражениям.
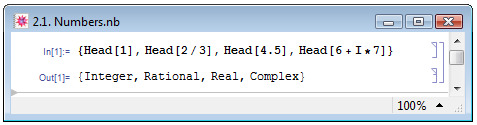
Для того чтобы определить, к какому типу относятся численные данные, следует воспользоваться специальной функцией Head — см. рис. 2.1.
"Целочисленные данные (Integer) – это целые числа, например 1, 2 или 123, которые представляются системой без погрешности и ограничения разрядности. Более того, арифметические операции над целыми числами система выполняет также без погрешностей и без ограничения числа цифр" (В. П. Дьяконов [2, с. 160]).
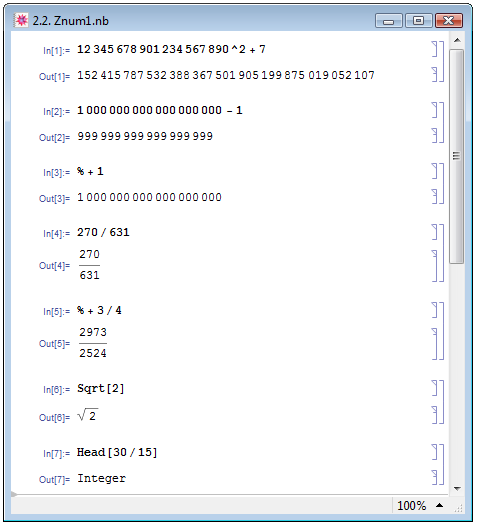
Количество цифр, задающих число, ограничено лишь его значением. Другой тип данных — рациональные данные — В. П. Дьяконов [2, с. 160] определяет следующим образом: "Рациональные данные задаются отношением целых чисел, например 123/567, и также представляют результат точно". Mathematica всегда, если это возможно, старается выдать точный результат — в виде целых или рациональных чисел — см. примеры на рис. 2.2.
Если во входной ячейке задана дробь, числитель и знаменатель которой являются целыми числами, причём числитель нацело делится на знаменатель, то это число является не рациональным, а целым. Так, например, число 30/15 является целым — см. пример In[7] на рис. 2.2.
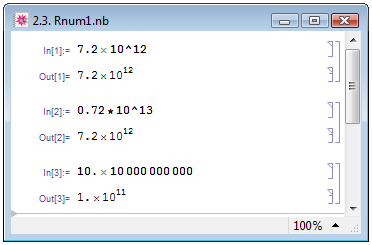
Вещественные данные задаются числами, которые в общем случае содержат мантиссу с разделёнными точкой целой и дробной частями и порядок, вводимый как степень числа 10 (В. П. Дьяконов [2, с. 160]). Вещественные числа могут иметь мантиссу с любым, но обязательно конечным числом знаков. Разделять мантиссу и порядок можно как знаком умножения " * ", так и пробелом, причём во втором случае в последних версиях Mathematica пробел автоматически заменяется обозначающим умножение крестиком " x ". Целая часть мантиссы, как отмечено в определении, отделяется от дробной части не запятой, а точкой (В. П. Дьяконов [2, с. 161]). Примеры задания вещественных данных см. на рис. 2.3.
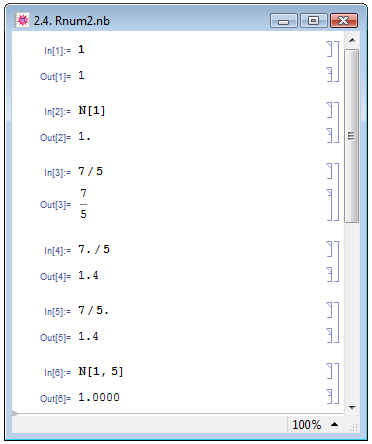
Добавление точки к любому целому числу или к числу в числителе и/или знаменателе рационального числа делает его в понимании Mathematica вещественным. Так, 1 есть целое число, но 1. — уже вещественное (ср. примеры In[1] и In[2] на рис. 2.4). Число 7/5 рассматривается как рациональное, но задание числителя как 7. и/или знаменателя как 5. делает его вещественным (ср. примеры In[3], In[4] и In[5]). Дабы представить некоторое выражение expr как вещественное число, используется функция N[ехрr,n], где n — количество цифр результата (пример In[6]).
Относительно вещественных чисел В. П. Дьяконов [2, с. 161] пишет следующее: "Вещественные числа всегда имеют некоторую погрешность представления результатов из-за неизбежного округления их и существования так называемого "машинного нуля" – наименьшего числа, которое воспринимается как нуль".
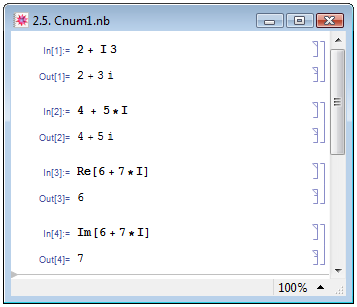
Одним из основных объектов в математике являются комплексные числа. Не обошли их вниманием и разработчики Mathematica. В Mathematica они задаются в виде z=Re[z]+I*Im[z], где I — мнимая единица (квадратный корень из -1), Re[z] — действительная часть комплексного числа z, а Im[z] — его мнимая часть (см. примеры In[1] и In[2] на рис. 2.5 задания комплексных чисел) (В. П. Дьяконов [2, с. 162]). Умножение мнимой единицы на мнимую часть комплексного числа задаётся явно — символом умножения " * " или пробелом. Выделить действительную и мнимую части заданного или полученного в результате вычислений комплексного числа z можно при помощи функций Re[z] и Im[z] соответственно (примеры In[3] и In[4]).
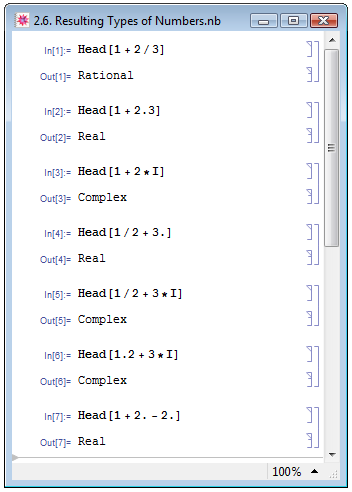
Если в процессе вычислений выполнялось арифметическое действие с числами разных типов, то тип результата вычислений зависит от типа исходных чисел. Проиллюстрируем эту зависимость на примере сложения. В примерах на рис. 2.6 при помощи Head мы будем определять тип результата сложения разнотипных числовых данных. Так сложение целого и рационального чисел в результате даёт рациональное число (пример In[1]), целого и вещественного — вещественное (пример In[2]), целого и комплексного — комплексное (пример In[3]), рационального и вещественного — вещественное (пример In[4]), рационального и комплексного — комплексное (пример In[5]), вещественного и комплексного — комплексное (пример In[6]). Таким образом, присутствие в вычислениях комплексного числа делает результат любого вычисления комплексным, присутствие в вычислениях вещественного числа (при отсутствии комплексного) делает результат вычисления вещественным. Следует отметить, что даже в таком экзотическом случае, когда к целому числу мы прибавляем вещественное число, а затем вычитаем это же вещественное число, результат вычислений всё равно будет вещественным (пример In[7])