Работа с графикой: визуализация функций одной переменной

Цель лекции: познакомиться с принципами создания в Mathematica двумерных графических объектов и работы с ними.

6.0. Введение

Сложно представить более наглядный способ представления данных, чем визуализация. Зачастую рисунки и графики скажут пользователю о предмете исследования гораздо больше, чем формулы и массивы данных. Именно поэтому разработчики Mathematica удели огромное внимание средствам визуализации и научили программу строить двух- и трёхмерные графики функций и дискретных наборов данных в виде численных массивов и т.д.

Любая математическая зависимость одной величины от другой может быть описана в Mathematica средствами двумерной графики. Именно с этими средствами мы познакомимся в данной лекции, построенной на основе книги Е. М. Воробьёва [1].

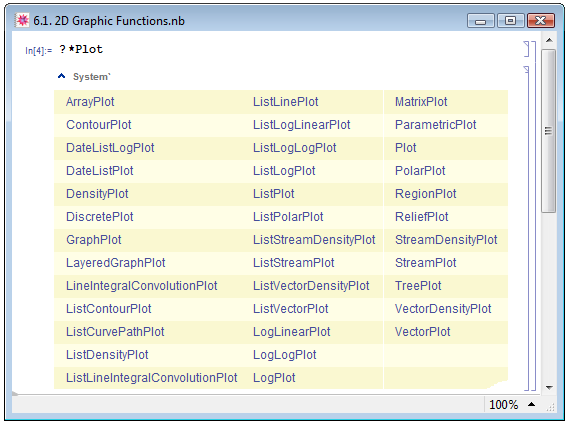
Встроенные функции Mathematica, предназначенные для работы с двумерной графикой, оканчиваются на Plot, поэтому для получения информации обо всех них непосредственно в Mathematica можно воспользоваться командой ?*Plot — рис. 6.1. Если мы сравним таблицу графических функций в ячейке Out[1] на рис. 6.1 с полученной аналогичным способом таблицей в книге Е. М. Воробьёва [1, с. 70], мы увидим, что в таблице в настоящей лекции содержится значительно больше функций. Поскольку данный курс писался с использованием пакета Mathematica более поздней версии, приведённое сравнение оказывается как нельзя лучшей наглядной иллюстрацией того, насколько динамично развивается Mathematica, ширится её функциональная палитра, растут возможности.

Безусловно, в рамках одной лекции мы не успеем познакомиться со всеми функциями, представленными на рисунке 6.1. Но мы и не ставим это своей задачей. Мы разберём функции, которые используются в Mathematica гораздо чаще других, а также, ввиду своей универсальности, могут взять на себя выполнения задач, для которых имеются свои узкоспециализированные функции.

Рис. 6.1. Функции Mathematica для создания двумерной графики

Все указанные на рис. 6.1 функции имеют чётко определённую структуру. Они имеют два обязательных аргумента и один необязательный. Первый обязательный аргумент есть выражение Mathematica, которое определяет зависимость (или зависимости), которую (которые) требуется построить. Второй аргумент, итератор, определяет аргументы функций и пределы их изменения. В трехмерном случае указываются два итератора. Необязательные аргументы графических функций — опций. Опциям присвоены значения по умолчанию, но если возникает необходимость, пользователь может задавать им собственные значения. Опции определяют стиль оформления, дополнительные параметры и элементы рисунков для повышения их большей наглядности и информативности.

6.1. Визуализация непрерывных математических функций

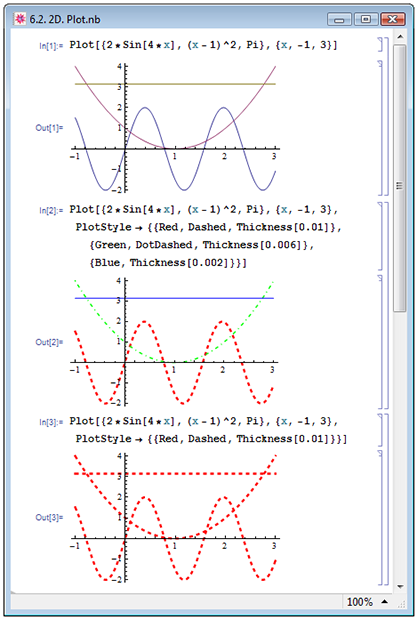
Первая функция, с которой мы познакомимся в настоящей лекции, являющаяся также наиболее часто используемой при работе с графикой, — это функция Plot. Заданная в простейшем виде Plot[func,{x,xmin,xmax}] она строит зависимость функции func от аргумента x, меняющегося в пределах от xmin до xmax. При помощи этой функции можно строить зависимости от одного аргумента сразу нескольких функций, для чего в качестве первого аргумента следует указать их список в виде {func1,func2,...}. В примере In[1] на рис. 6.2 мы построили на одном графике зависимости тригонометрической функции и параболы от меняющегося в пределах от -1 до 3 аргумента x, а также параллельную оси абсцисс прямую, характеризующую постоянное значение Pi.

Подробней о функции Plot см. книги Е. М. Воробьёва [1, с. 71, 76–77] и А. Н. Прокопени и А. В. Чичурина [5, с. 43–46].

По умолчанию Mathematica рисует все графики сплошными линиями одинаковой толщины, различаются только цвета: график первой в списке функции строится синим, второй — фиолетовым, третий — бежевым и т.д. Для того чтобы различать графики, используется специальная опция, которая, как и все опции графических функций, задаётся при помощи правил преобразования в виде PlotStyle->{{set1},{set2},...}, где set1,set2,... — набор графических директив (отличительных свойств) для графика с соответствующим номером 1,2,.... Под графическими директивами понимаются выражения, влияющие на характеристики графических объектов. Директивами могут выступать толщина линии, тип линии (линия может быть сплошная, штриховая, точечная и т.д.), цвет. В примере In[2] построим те же графики, что и в In[1], но изобразим их отличным друг от друга образом: первый график сделаем пунктирным при помощи директивы Dashed, красным при помощи Red и зададим при помощи директивы Thickness[d] относительную толщину линии d равную, например, 0.01; второй график сделаем зелёным, Green, штрихпунктирным, DotDashed, и более тонким (0.006); третий график оставим сплошным, не задавая для типа линии никаких дополнительных директив, но сделаем его синим, Blue, и самым тонким из трёх (0.002). Сравнение примеров Out[1] и Out[2] даёт яркое представление влияния опции PlotStyle на возвращаемое функцией Plot изображение.

Если опция PlotStyle задана в виде одномерного списка, PlotStyle->{dir1,dir2,...}, то каждая директива, независимо от её типа, будет относиться только к зависимости с соответствующим номером. Т.е., внешний вид первого графика будет определяться только директивой dir1, второго — только директивой dir2 и т.д.

Если для какого-то графика не нужно указывать дополнительных директив, то на месте соответствующего элемента вложенного списка в опции PlotStyle указывается пустой список {}.

Если в опции PlotStyle указан только один набор графических директив (PlotStyle задана как вложенный список, содержащий только один элемент), то он относится ко всем графикам. Так в примере In[3] на рис 6.2 мы сделали линии всех графиков красными, штриховыми, толщины 0.01.

Подробней об опции PlotStyle см. книги Е. М. Воробьёва [1, с. 76–77] и А. Н. Прокопени и А. В. Чичурина [5, с. 50–51].

увеличить изображение
Рис. 6.2. Функция Plot для построения функции одной переменной

Е. М. Воробьёв [1, с. 77] отмечает, что к построению графиков функций возможны два подхода, "две стратегии". Первый подход заключается в том, что сначала определяются характерные точки графика, а затем вычисляются функции в этих точках. Именно этим подходом обычно пользуется Mathematica.

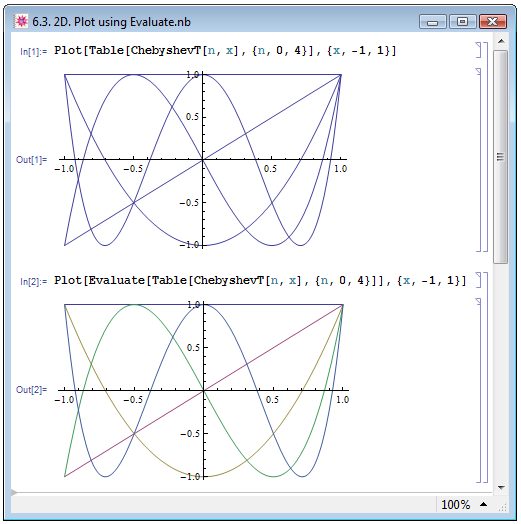
Во втором подходе сначала получается наиболее простое приближение для функции в заданном интервале, а затем вычисляются приближённые значения в некотором наборе точек из этого интервала. Заставить программу вторым путём можно, применив к вычисляемому выражению func функцию Evaluate[func]. Она вынуждает программу вычислять выражение func даже в случае, если оно является аргументом функции, атрибуты которой устанавливают, что это выражение должно оставаться невычисленным. Наглядно представим действие этой функции. В качестве функции для визуализации, как и Е. М. Воробьёв [1, с. 79], возьмём полином Чебышева. На рис. 6.3 построим графики первых десяти полиномов Чебышева, при этом в примере In[1] обойдёмся без функции Evaluate[func], а в примере In[2] применим её к полиномам. Как мы видим, в первом случае Mathematica изобразила графики всех зависимостей одним цветом, то есть, при вычислении она считала точки всех зависимостей принадлежащими одному графику. Во втором случае графики зависимостей для всех полиномов различны, поскольку, согласно второму подходу, Mathematica сначала определилась с функциями, зависимости которых будет строить, и только потом вычислила их значения в некоторых точках интервала. Таким образом, все зависимости рассматривались программой в отдельности друг от друга.

Рис. 6.3. Функция Evaluate: изменение подхода к построению графиков

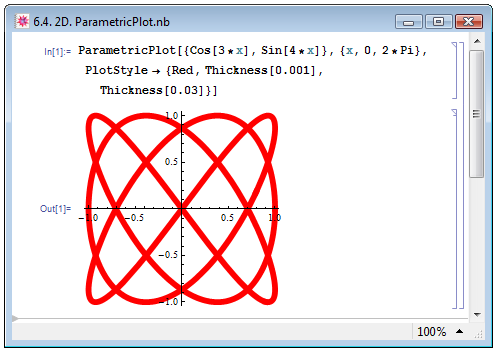
Зачастую требуется строить не зависимость функции от её аргумента, а зависимость одной функции от другой, зависящей от того же аргумента, то есть, строить параметрическую зависимость. Для этого в Mathematica имеется функция ParametricPlot. Её описание полностью совпадает с описанием функции Plot за исключением следующего момента: для построения графика одной зависимости первый аргумент задаётся в виде списка {funcarg,func}, при этом при построении значения функции funcarg откладываются по оси абсцисс, а func — по оси ординат; при построении графиков нескольких зависимостей аргумент задаётся в виде вложенного списка {{funcarg1,func1},{funcarg2,finc2},...}. На рис. 6.4 мы приводим параметрическую зависимость 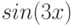от , характеризующую поведение точки, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях — прочерчивающей так называемые фигуры Лиссажу (см. похожий пример в работе Е. М. Воробьёва [1, с. 79]).

Подробней о функции ParametricPlot см. книги Е. М. Воробьёва [1, с. 79] и А. Н. Прокопени и А. В. Чичурина [5, с. 55–56].

Рис. 6.4. Построение графиков параметрических зависимостей при помощи функции ParametricPlot

В примере на рис. 6.4 мы снова воспользовались опцией PlotStyle, сделав линии на графике красными при помощи уже известной нам директивы Red и толстыми при помощи директивы Thickness[0.03].

Кроме того, мы проиллюстрировали тот факт, что если в списке директив, относящихся к одному и тому же изображению, содержатся директивы, противоречащие друг другу (в нашем случае это директивы Thickness[0.001] и Thickness[0.03], устанавливающие разную толщину линий), то при построении применяется та, которая указана в списке последней (Thickness[0.03]).

Подробней об описанных директивах см. книгу А. Н. Прокопени и А. В. Чичурина [5, с. 50–51].

С другими опциями двумерных графических функций мы познакомимся в следующем пункте настоящей лекции.

Если функция задана не в декартовых, а в полярных координатах, то адекватно изобразить её позволит функция PolarPlot[r,{teta,tetamin,tetamax}], где r — характеризующий кривую радиус, зависящий от угла teta; угол меняется в пределах от tetamin до tetamax. Если требуется изобразить несколько кривых, то в качестве первого аргумента указывается список радиусов, описывающих кривые, {r1,r2,...}. Внешний вид генерируемых этой функцией рисунков можно менять при помощи опций, аналогичных опциям функций Plot и ParametricPlot. На рис. 6.5 приведён пример построения зависимости в полярных координатах при помощи функции PolarPlot.

Подробней о функции PolarPlot см. Е. М. Воробьёва [1, с. 76].

Рис. 6.5. Визуализация непрерывной зависимости в полярных координатах