Функциональное программирование

Цель лекции: познакомиться с основами реализации функционального стиля программирования в языке программирования Mathematica

9.0. Введение

Хотя Mathematica предназначена, по большей части, для решения математических задач без применения программистских навыков, и всёже она позволяет при необходимости использовать программирование в случаях, когда имеющихся встроенных функций оказывается недостаточно, или в случае, если требуется создать собственный оригинальный алгоритм для их решения. Фактически, Mathematica является ориентированным на математические расчеты языком программирования сверхвысокого уровня. Следует подчеркнуть, что речь идет не о языке реализации самой системы Mathematica (коим является C++), а о системе как языке программирования самой по себе. Mathematica является типичным интерпретатором и не предназначена для создания исполняемых файлов.

Как отмечает Е. М. Воробьёв [1, с. 125], поскольку Mathematica является языком программирования, то написание программ — наиболее логичная форма взаимодействия с ней. Mathematica позволяет программировать в трех стилях:

• функциональном;
• процедурном;
• стиле, основанном на создании правил преобразований

В данной лекции мы рассмотрим функциональный стиль программирования, за основу взяв книги Е. М. Воробьёва [1], П. Веллина и др. [14] и С. Мангано [11].

В Mathematica имеется более 1000 встроенных функций. Хотя каждая функция осуществляет достаточно узкоспециализированные операций, в своей совокупности они позволяют выполнять широчайший набор действий. Конкретные действия выполняются определённой комбинацией встроенных функций, и если то или иное действие достаточно часто встречается при проведении расчётов, было бы удобно применение комбинации функций заменить применением всего-навсего одной функции. Это стремление, по сути, лежит в основе функционального программирования.

9.1. Функции для управления выражениями

В предыдущих лекциях мы научились применять встроенные функции Mathematica к выражениям, пользуясь их внутренним представлением в виде h[e1,e2,…] или операторной формой (например, операторы сложения " + " и вычитания " - "). Однако существует ещё один менее наглядный, менее интуитивный, но крайне необходимый для функционального программирования способ управления выражениями. Заключается он в применении ряда специальных функций, инициирующих действие других функций.

9.1.1. Функция Map

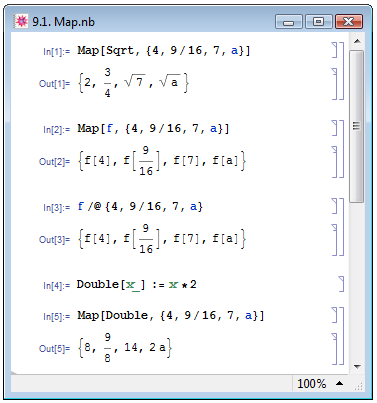
Функция Map[func,expr] применяет функцию func к каждому элементу выражения expr, если оно является списком, или непосредственно к выражению expr в остальных случаях. В примере In[1] на рис. 9.1 при помощи функции Map мы применили встроенную функцию извлечения квадратного корня Sqrt к элементам списка {4,9/16,7,a}. В примере In[2] первым аргументом Map мы указали ранее не определённое в качестве функции выражение f, но Mathematica самостоятельно расценила его как функцию и также применила к элементам заданного списка.

К функции Map можно обратиться в постфиксной форме: для того чтобы применить функцию func к выражению expr, следует записать следующее выражение func/@expr. В примере In[3] на рис. 9.1 мы выполняем то же действие, что и в In[2], но пользуемся постфиксной формой записи функции Map.

При помощи Map к выражениям можно также применять и функции, заданные пользователем. Задавать функции самостоятельно мы научимся чуть позже, а сейчас на рис. 9.1 приведём лишь пример In[4] задания функции, удваивающей выражение, указанное в качестве её аргумента (назовём функцию Double), а в примере In[5] применим её к нашему списку при помощи функции Map.

Рис. 9.1. Функция Map при работе с одномерными списками

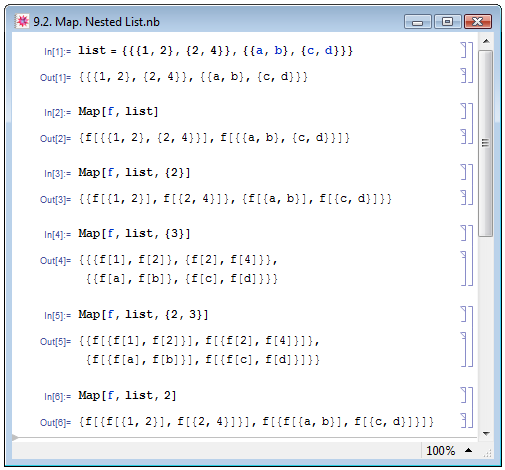
Если вторым аргументом expr в Map[func,expr] является вложенный список, то указанная в первом аргументе функция func будет применена к элементам списка первого уровня. В примере In[1] на рис. 9.2 мы задали трёхуровневый список, к которому в примере In[2] применили неопределённую ранее функцию f. Для того чтобы применить func только к элементам внутреннего списка конкретного уровня, следует задать третий аргумент, и тогда функция Map будет выглядеть следующим образом: Map[func,expr,listlevel]. Если выражение listlevel задано в фигурных скобках, {listlevel}, то функция func будет применена только к элементам внутреннего списка уровня listlevel. В примерах In[3] и In[4] мы применяем функцию f к элементам внутренних списков второго и третьего уровней, соответственно.

Если третий аргумент функции Map задан в виде списка {listlevelst,listlevelfin}, то функция func применяется к элементам внутренних списков от уровня listlevelst до listlevelfin. В примере In[5] на рис. 9.2 мы применяем функцию f к элементам внутренних списков от второго уровня до третьего.

Если listlevel задан без фигурных скобок, то функция func будет применена к элементам всех уровней от первого до listlevel включительно. В примере In[6] мы применяем f к элементам списков до второго уровня.

Подробней о функции Map см. книги Е. М. Воробьёва [1, с. 118–120] и П. Веллина и др. [14, с. 78–79].

Рис. 9.2. Функция Map при работе с вложенными списками