Функциональное программирование

9.2. Суперпозиция функций

9.2.1. Итерационные функции

В математике композиция (суперпозиция) функций — это применение одной функции к результату другой. Частным случаем такой операции является применение к выражению одной и той же функции несколько раз.

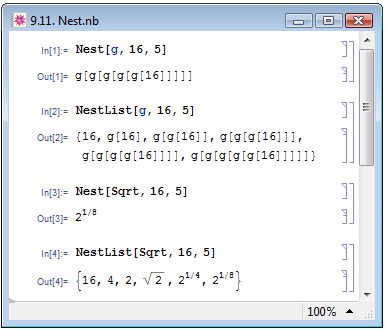
Функция Nest[func,exps,n] последовательно применяет n раз функцию func к выражению expr. Для того чтобы проследить за процессом получения конечного выражения, используется функция NestList с теми же аргументами. Эта функция генерирует список результатов, полученных при применении функции func к выражению expr на каждой итерации. На рис. 9.11 мы воспользовались функциями Nest и NestList для того, чтобы пять раз применить к выражению 16 неопределённую функцию g (примеры In[1] и In[2]) и функцию вычисления квадратного корня Sqrt (примеры In[3] и In[4]). Результаты вычислений в ячейках Out[1] и Out[3], как и ожидалось, совпадают с последними элементами списков в Out[2] и Out[4], соответственно.

Рис. 9.11. Использование итерационных функций Nest и NestList

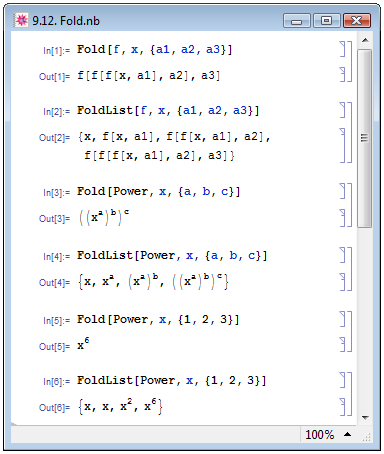
Функции Fold и FoldList работает с функциями двух аргументов. Заданная в виде Fold[func,var,{a1,a2,…}] функция на первой итерации применяет функцию func к аргументам var и a1, на второй итерации применяет func к результату предыдущей итерации и аргументу a2 и так далее, до последнего элемента в списке. На рис. 9.12 приведены примеры использования функций Fold и FoldList для неопределённой функции f (примеры In[1] и In[2]) и функции возведения в степень Power (примеры In[3] – In[6]).

Подробней об итерационных функциях см. книги Е. М. Воробьёва [1, с. 132–134] и П. Веллина и др. [14, с. 86–87].

Рис. 9.12. Использование итерационных функций Fold и FoldList

9.2.2. Композиция нескольких функций

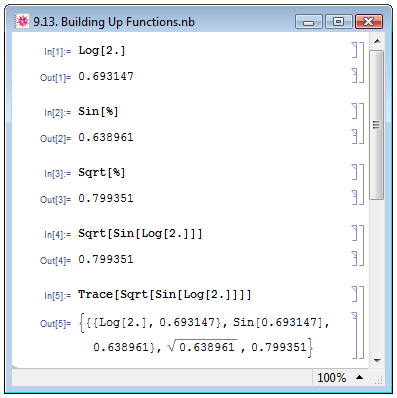
В более широком смысле композиции функций в качестве аргумента функции можно использовать результат выполнения другой функции. В Mathematica последовательное применение к выражению нескольких функций называется вызовом вложенной функции (nested function call) (П. Веллин и др. [14, с. 89]). В примере на рис. 9.13 сначала мы применили к числу 2. функцию Log (пример In[1]), а затем к полученному результату последовательно — функции Sin и Sqrt (примеры In[2] – In[3]). Однако все указанные операции можно совершить за одно действие. В примере In[4] мы вызываем вложенную функцию Sqrt[Sin[Log[2.]]]: сравнив выходные данные в Out[3] и Out[4], мы убедимся, что оба подхода применения к аргументу последовательно нескольких функций приводят к одинаковому результату.

Когда мы пользуемся первым подходом, мы можем проследить за процессом вычисления, поскольку помимо конечного результата получаем промежуточные результаты действия каждой функции (в нашем случае это Out[1] и Out[2]). Для получения промежуточных результатов при использовании второго подхода используется функция Trace. В примере In[5] на рис. 9.13 мы применяем Trace к вложенной функции In[4].

Рис. 9.13. Вычисления с использованием вложенных функций

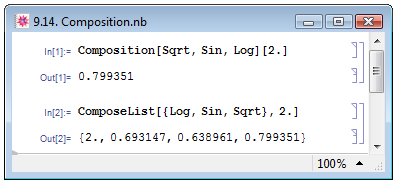
Композицию функций можно осуществлять менее наглядным, но более традиционным для Mathematica способом — при помощи встроенной функции Composition. Указывается она в следующем виде: Composition[func1,func2,...][arg], где funci — функции в порядке, обратном порядку их применения к аргументу (или аргументам) arg, т.е., последней применяется функция func1, предпоследней — func2 и т.д. В примере In[1] на рис. 9.14 при помощи Composition мы осуществляем тот же набор действии, что и на рис. 9.13.

Для получения промежуточных результатов выполнения вложенной функции при данном подходе используется функция ComposeList[{func1,func2,...},arg]. Однако, у ComposeList порядок функций в аргументе обратный в сравнении с Composition: функция func1 применяется первой — ср. примеры In[1] и In[2] на рис. 9.13. Также обратим внимание на то, что формат вывода результата данных функциями Trace и ComposeList различный: если в первом случае мы имеем вложенный список, содержащий как вычисляемое выражение в явном виде, так и результат вычислений, то во втором — одномерный список с результатами вычислений.

Подробней о композиции функций см. книгу Е. М. Воробьёва [1, с. 134–136].

Рис. 9.14. Задание вложенных функций при помощи функции Composition и ComposeList