Работа с графикой: визуализация функций одной переменной

6.3. Визуализация дискретных зависимостей

Функция DiscretePlot, которую мы рассмотрим следующей, является некоторым промежуточным звеном между функциями визуализации непрерывных зависимостей и функциями визуализации дискретного набора данных. Заданная в простейшем виде DiscretePlot[expr,{i,imax}], она визуализирует значения выражения expr при i, принимающем значения от 1 до nmax с шагом 1. Таким образом, expr представляет собой некоторую функцию от i, но i принимает дискретные значения.

Указанный вторым аргументом итератор может быть задан в иной форме. При {i,imin,imax} значение i меняется от imin до imax с шагом 1, а при {i,imin,imax,di} — с шагом di.

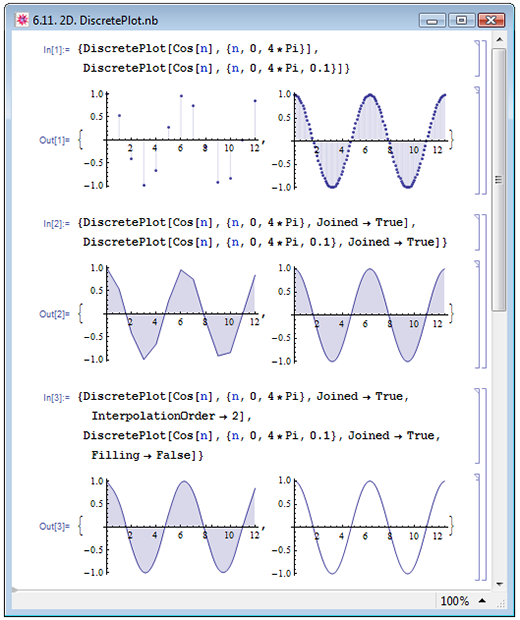
На рис. 6.11 приведён пример построения дискретного набора значений функции Cos[n] для n, принимающего значения от 0 до 4*Pi. В In[1] на рисунке слева мы ограничились стандартными шагом изменения переменной n, равным единице, а на рисунке справа уменьшили шаг на порядок.

Для того чтобы дискретная зависимость была более наглядной, построенные точки можно соединить, указав опцию Joined->True. В примере In[2] на рис. 6.11 мы перестроили оба рисунка In[1], соединив построенные точки. Если на рисунке справа действительно изображена весьма правдоподобная косинусоида, то угловатые айсбергоподобные пеньки на рисунке слева вызывают некоторое недоумение. Дело в том, что по умолчанию Mathematica соединяет соседние точки отрезками прямой. Именно поэтому при малом количестве построенных точек линия оказывается ломаной. Однако можно заставить Mathematica соединять точки гладкими кривыми — сплайнами. При этом порядок r кривых можно задать самостоятельно при помощи опции InterpolationOrder->r. В примере In[3] на левом рисунке мы соединили линии кривыми второго порядка, задав InterpolationOrder->2. При построении правого рисунка в In[3] мы воспользовались уже известной нам опцией Filling. Если мы вновь обратим внимание на построенные нами на рис. 6.11 изображения, то мы увидим, что области между построенными изображениями и осью абсцисс заполнены цветом. Если точки соединены линиями, то заполнено всё пространство под кривой, а от отдельно стоящих точек к оси абсцисс проведена нормаль. Опция Filling->False отключает автоматическое закрашивание областей под построенными изображениями.

увеличить изображение
Рис. 6.11. Визуализация дискретных зависимостей при помощи функции DiscretePlot

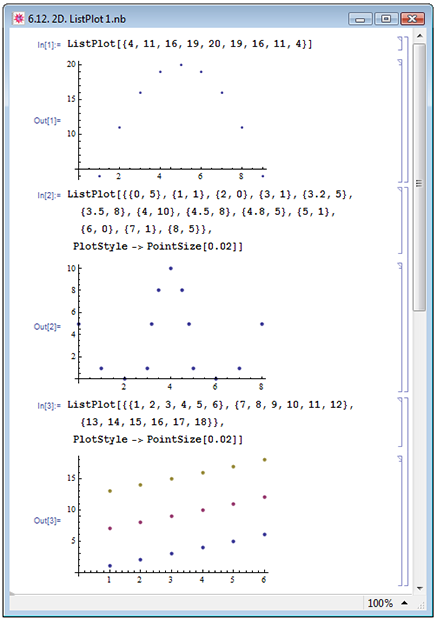
Итак, мы научились визуализировать аналитически заданные функции одной переменной. Однако аналитический вид зависимости не всегда может быть известен. Зависимость может быть задана дискретным набором данных, в виде списка. Для визуализации заданных таким образом зависимостей используется функция ListPlot. Обязательным аргументом функции должен быть список, описывающий множество точек зависимости. Список может быть одномерным, list1={y1,y2,...}, вложенным в виде матрицы, list2={{x1,y1},{x2,y2},...}: в первом случае графически будет представлено множество точек с координатами {i,yi} (пример In[1] на рис. 6.12), а во втором — с координатами {xi,yi} (пример In[2], в котором мы также изменили диаметр ddot точек на графике при помощи директивы PointSize[ddot]).

Если внутренние списки аргумента функции ListPlot содержат больше двух элементов, list3={{y11,y12,...},{y21,y22,...},...} ,то все они рассматриваются как отдельные наборы данных. Так в примере In[3] на рис. 6.12 заданный таки способом вложенный список был визуализирован как три отдельные зависимости: именно поэтому соответствующие им точки имеют разные цвета.

Список можно формировать непосредственно при обращении к графической функции при помощи рассмотренных нами в лекции 3 функций, например, Table.

увеличить изображение
Рис. 6.12. Визуализация дискретных зависимостей при помощи функции ListPlot

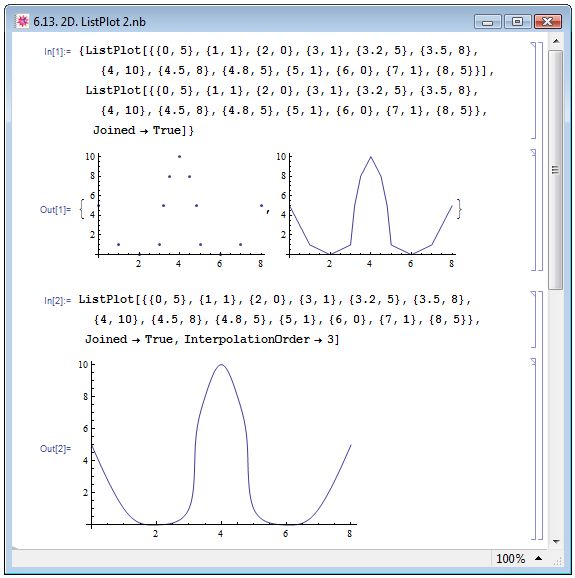
Если рисунок с отдельно стоящими точками недостаточно нагляден, точки можно соединить между собой в том порядке, в каком они указаны в списке. Делается это заданием уже знакомой нам опции Joined->True (ср. правый и левый рисунки в примере In[1] на рис. 6.13). Безусловно, линия, соединяющая отдельно стоящие точки дискретной зависимости, получается ломаной. Сделать график сглаженным позволяет ещё одна известная нам опция InterpolationOrder->n. В примере In[2] мы интерполировали зависимость, заданную в предыдущем примере, кривыми третьего порядка.

Рис. 6.13. Соединение точек дискретных зависимостей

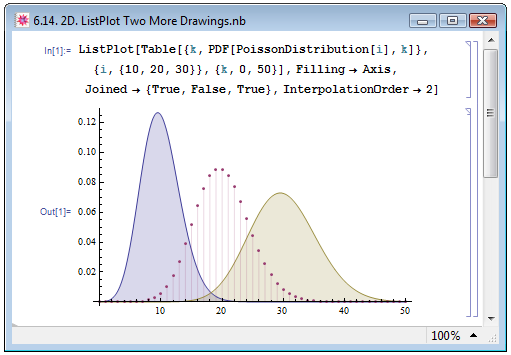
ListPlot также позволяет изображать на одном рисунке сразу несколько зависимостей, при этом в качестве аргумента следует указать зависимости в виде списка {list1,list2,...}. В примере In[1] на рис. 6.14 мы визуализировали распределение Пуассона для трёх различных значений среднего. При этом, точки только двух графиков из трёх мы соединили линиями, Joined->{True,False,True}, и интерполировали квадратичными сплайнами, InterpolationOrder->2. Кроме того, мы включили заполнение областей между линиями графиков и осями Filling->Axis. Как мы видим, области под графиками, точки которых соединены, заполнены полностью. Что касается оставшегося графика, то заполнение области под ним ограничилось лишь проведением нормалей из этих точек к оси абсцисс.

Рис. 6.14. Визуализация нескольких дискретных зависимостей

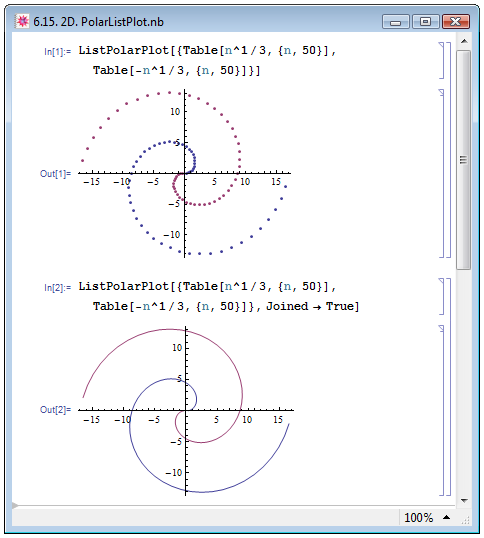
Для дискретных данных также имеется функция построения зависимости в полярных координатах — ListPolarPlot[r,{teta,tetamin,tetamax}], где r — характеризующий кривую радиус, зависящий от угла teta; угол меняется в пределах от tetamin до tetamax. Функция также позволяет изобразить несколько кривых, задав первый аргумент в виде {r1,r2,...}. Пример использование функции ListPolarPlot приведён на рис. 6.15.

Подробней о функциях визуализации дискретных зависимостей см. книги Е. М. Воробьёва [1, с. 80–81] и А. Н. Прокопени и А. В. Чичурина [5, с. 56–58].

Рис. 6.15. Визуализация дискретной зависимости в полярных координатах