| Россия, Новосибирск, НГПУ, 1994 |
Символьные вычисления
5.3.3. Пределы
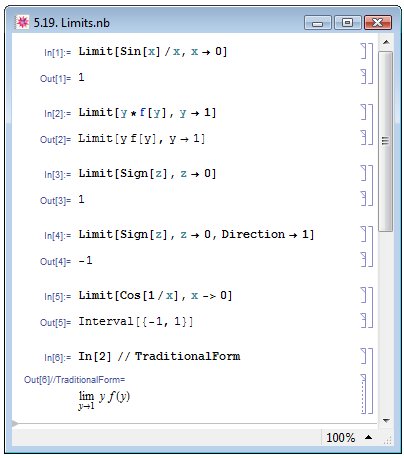
Вычислить предел некоторой функции f[var] при стремлении var к заданному значению var0 позволяет функция Limit[f[var],var->var0]. Предел вычисляется только для функций, заданных в явном виде, в противном случае в ячейке Out возвращается исходное выражение — примеры In[1] и In[2] на рис. 5.19.
Предел ряда функций при стремлении var->var0 зависит от направления, вдоль которого осуществляется приближение var к var0. Требуемое направление задаётся опцией Direction->s, где при вычислении предела сверху вместо s следует писать -1, а снизу — 1. Для значения Automatic, используемого по умолчанию, вычисляется предел сверху, кроме случая var->Infinity (примеры In[3] и In[4] на рис. 5.19) [5, с. 40].
При стремлении var к некоторому var0 предельное значение функции f[var] не всегда существует. А.Н. Прокопеня и А.В. Чичурин [5, с. 41] приводят следующий пример: "Функция 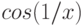 , например, является быстро осциллирующей при
, например, является быстро осциллирующей при 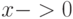 . Поэтому результатом вычисления соответствующего предела является Interval-объект, который только указывает интервал, в пределах которого может находиться вычисляемый предел". Иллюстрирующий это замечание пример In[5] на рис. 5.19 также аналогичен примеру в книге А. Н. Прокопени и А. В. Чичурина [5, с. 41].
. Поэтому результатом вычисления соответствующего предела является Interval-объект, который только указывает интервал, в пределах которого может находиться вычисляемый предел". Иллюстрирующий это замечание пример In[5] на рис. 5.19 также аналогичен примеру в книге А. Н. Прокопени и А. В. Чичурина [5, с. 41].
Mathematica позволяет представлять на экране выражение для нахождения предела в традиционном для математики виде. Для этого служит функция TraditionalForm. В примере In[6] на рис. 5.19 мы в традиционной форме представили предел, записанный в In[2].
Подробней о функции нахождения предела см. книгу А. Н. Прокопени и А. В. Чичурина [5, с. 40–41].
Ключевые термины
Подстановки — это алгебраические преобразования, в результате выполнения которых какая-либо часть алгебраического выражения заменяется новым выражением.
Рациональным выражением называется дробь, числитель и знаменатель которой — полиномы.
Краткие итоги
В данной лекции мы научились осуществлять преобразования выражений, в том числе рациональных и тригонометрических. В частности мы познакомились с функциями, предназначенными для раскрытия произведений и положительных степеней сумм, упрощения выражений. Мы научились компьютерными методами распознавать среди выражений полиномы, собирать члены полиномов при нужных степенях, находить наименьшее общее кратное и наибольший общий делитель полиномов. Мы познакомились с одним из наиболее эффективных инструментов осуществления преобразований выражений — подстановками. Мы познакомились со встроенными функциями Mathematica, позволяющими осуществлять операции математического анализа, в том числе находить производные, первообразные, суммы и произведения, раскладывать функции в ряд и находить пределы.
Вопросы
- Какие преобразования многочленов позволяет выполнять Mathematica? С помощью каких функций?
- Какое преобразование многочлена Mathematica осуществляет при помощи функции Expand? Factor? FactorTerms? Collect? Simplify?
- В чём отличие функции Factor от FactorList? FactorTerms от FactorTermsList?
- Для чего предназначена опция Trig функций Factor и Expand?
- Каким образом можно проверить, является ли то или иное выражение многочленом для некоторой переменной?
- Какое действие оказывают функции Expand, Factor, Together, Apart, на рациональные выражения?
- Какие функции позволяют обращаться только к числителю или только к знаменателю рационального выражения?
- С помощью какой функции Mathematica позволяет выражать тригонометрические выражения через экспоненты? записывать экспоненты комплексных аргументов через тригонометрические функции?
- Что такое подстановка в Mathematica? Чем отличается глобальная подстановка от локальной?
- При помощи каких функций осуществляется подстановка в Mathematica?
- Назовите функции Mathematica, позволяющие выполнять операции математического анализа.
Упражнения
- Пользуясь функциями преобразования многочленов, из многочлена
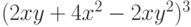 получите следующие выражения:
получите следующие выражения:
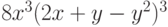
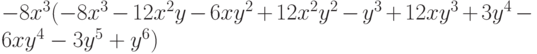
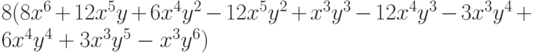
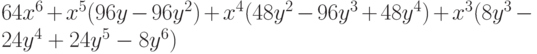
При помощи функции Length определите количество элементов в каждом полученном выражении. Какой заголовок находится на верхнем уровне полной формы каждого из полученных выражений?
- Дано исходное выражение
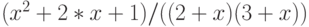 . Пользуясь функциями преобразования многочленов и рациональных выражений,
. Пользуясь функциями преобразования многочленов и рациональных выражений, - представьте исходное выражение в виде суммы дробей с одинаковым знаменателем;
- разложите на множители числитель и знаменатель исходного выражения;
- разложите исходное выражение на сумму простых дробей;
- найдите наименьшее общее кратное и наибольший общий делитель числителя и знаменателя исходного выражения.
- Пользуясь локальной подстановкой, в выражении
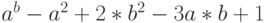 символ
символ  замените символом
замените символом  , а символ
, а символ  — выражением
— выражением 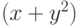 .
. - Пользуясь подстановками
 и
и  , преобразуйте исходное выражение
, преобразуйте исходное выражение  к выражению, не содержащему иных символов, кроме
к выражению, не содержащему иных символов, кроме  .
. - Разложите выражение
 в степенной ряд по степеням
в степенной ряд по степеням  возле точки
возле точки 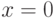 до члена c
до члена c 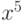 , найдите производную полученного выражения по
, найдите производную полученного выражения по  .
. - Пользуясь полученными в данной и предыдущих лекциях навыками, следуя указанным комментариям, решите заданные ниже уравнения. Проверьте правильность полученных корней, подставив их в исходные уравнения.
- )квадратное уравнение
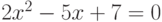 .
.
Для решения сначала вычислите дискриминант по формуле
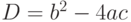 , затем найдите корни уравнения по формулам
, затем найдите корни уравнения по формулам 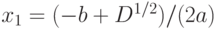 и
и 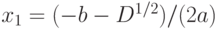 . Корни уравнения могут быть комплексными.
. Корни уравнения могут быть комплексными. - квадратное уравнение
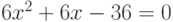 .
.
Решите двумя способами.
Первый способ — аналогично предыдущему пункту.
Второй способ: при помощи функций Mathematica преобразования многочленов разложите выражение в левой части уравнения на множители.
- возвратное кубическое уравнение
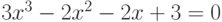 .
.
Для решения при помощи функций Mathematica преобразования многочленов разложите выражение в левой части уравнения на множители.
- биквадратное уравнение
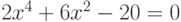 .
.
Для решения при помощи локальной подстановки замените
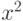 символом
символом  , затем известным способом решите квадратное уравнение относительно
, затем известным способом решите квадратное уравнение относительно  .
. - дифференциальное уравнение первого порядка с разделяющимися переменными
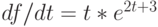 .
.
Для решения перенесите дифференциал
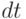 в правую часть, средствами Mathematica проинтегрируйте обе части по соответствующим переменным.
в правую часть, средствами Mathematica проинтегрируйте обе части по соответствующим переменным. - линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
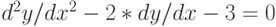 .
.
Для решения сначала найдите корни характеристического уравнения, полученного заменой выражения
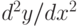 символом
символом 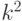 , а выражения
, а выражения 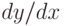 символом
символом  . Полученные корни подставьте в общее решение уравнения
. Полученные корни подставьте в общее решение уравнения 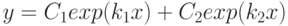 .
.
- )квадратное уравнение
- найдите площадь криволинейной трапеции, ограниченной
- графиком функции
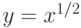 , осью
, осью  , прямыми
, прямыми 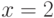 и
и 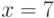 ;
; - графиком функции
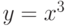 , осью
, осью  и прямой
и прямой 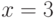 ;
; - графиком функции
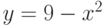 и осью
и осью  .
. - найдите площадь фигуры, ограниченной графиками функций
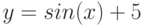 и
и 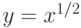 , прямыми
, прямыми 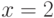 и
и 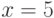 .
.
- графиком функции
- Найдите пределы следующих выражений:
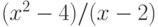 при
при 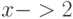
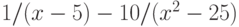 при
при 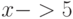
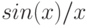 при
при 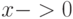
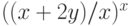 при x->\infty
при x->\infty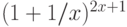 при x->\infty
при x->\infty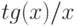 при
при