Работа с числами

4.5. Работа с массивами чисел

Зачастую пользователи работают не с отдельными числами, а с некоторым массивом данных, причём эти массивы могут быть достаточно большими, что создаёт определённые трудности в работе с ними. Mathematica использует два особых типа данных, делающих работу с массивами чисел быстрее и эффективнее, — это разреженные массивы и уплотнённые массивы.

4.5.1. Разреженные массивы

При решении множества задач, в частности, при решении обыкновенных дифференциальных уравнений и уравнений в частных производных, больших систем уравнений, а также задач оптимизации, приходится нередко работать с матрицами высокого порядка, которые при этом содержат большое количество нулевых элементов. Подобные матрицы могут быть преобразованы в разреженные массивы — массивы, в которых не все элементы используются, имеются в наличии или нужны в данный момент; большое количество алгоритмов разработано специально для работы с такими объектами.

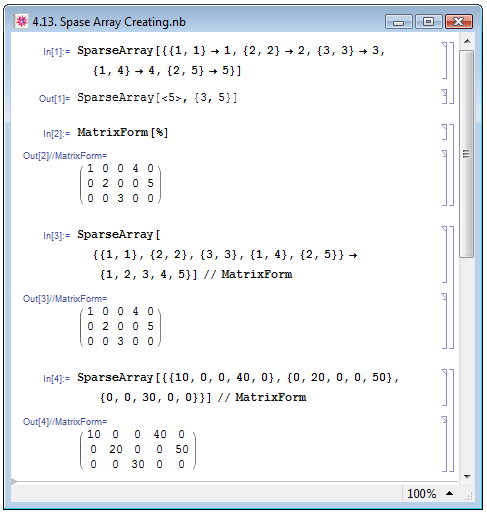
Разреженные массивы создаются при помощи функции SparseArray. Заданная в простейшей форме, функция SparseArray[{pos1->val1,pos2->val2,...}] генерирует массив, в котором значение pos1 занимает позицию val1, pos2 — позицию val2, и т.д., то есть, весь массив мы от начала и до конца задаём вручную, самостоятельно вводя данные. При этом размерность массива определяется автоматически: в примере In[1] на рис. 4.13 мы задаём двумерный массив, число строк которого определяется наибольшим значением первого элемента списков pos1,pos2,... (в нашем случае оно равно 3), а число столбцов, соответственно, наибольшим значением второго элемента (5 в нашем примере).

Точно такого же результата можно добиться, задав функцию в виде SparseArray[{pos1,pos2,...}->{val1,val2,...}], при этом значения val1,val2,... также занимают соответствующие позиции pos1,pos2,... — пример In[3] на рис. 4.13. При такой форме задания разреженного массива количество позиций pos должно совпадать с числом присваиваемых значений val.

В редуцированной форме функция SparseArray[{pos1,pos2,...}->val] на каждую позицию pos1,pos2,... помещает значение val.

Как разреженные массивы Mathematica рассматривает только объекты, созданные при помощи функции SparseArray. Массивы, созданные при помощи функций, с которыми мы познакомились в лекции 3, будут рассматриваться как обычные списки. Однако такие списки list можно преобразовать в разреженные массивы, применив к ним функцию SparseArray[list] — пример In[4] на рис. 4.13. Если список list является вложенным, то его внутренние списки должны иметь одинаковое число элементов, т.е., в двумерном случае list должен быть матрицей.

Рис. 4.13. Задание разреженных списков

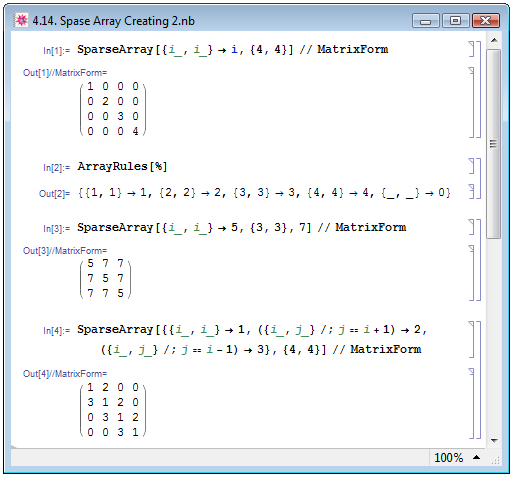
Наиболее широко употребимо задание функции в виде SparseArray[data,{d1,d2,..}], которая генерирует массив объектов размерностью d1xd2x..., причём всем позициям, значения которым не присвоены в аргументе data, присваивается значение 0. Например, в примере In[1] на рис. 4.14 мы задаём массив 4x4, диагональным элементам которого присвоено значение номера строки (или столбца, поскольку они равны), а остальным элементам — 0.

Узнать, по каким правилам присвоены значения элементам массива mass можно при помощи функции ArrayRules[mass]. В нашем примере Out[2] на рис. 4.14 мы видим, что ячейкам с конкретными номерами присвоены конкретные значения, а запись {_,_}->0 означает, что всем ячейкам, для которых никаких иных правил не задано, и присваивается значение 0.

Присваиваемое пустым (неупомянутым в аргументе data) ячейкам значение не обязательно должно быть 0: его можно определять самостоятельно при помощи третьего аргумента val0 функции SparseArray[data,{d1,d2,..},val0] — пример In[3] на рис. 4.14.

Выбирать ячейки, которым будет присваиваться значение, можно и более избирательно, задавая в аргументе data более пространные условия. Так в примере In[4] на рис. 4.14 при помощи неоднократно используемого нами условия заполнили главную диагональ числом 1, диагональ выше неё — при помощи условия ({i_,j_}/;j==i+1)->2 числом 2, а диагональ ниже — числом 3.

Рис. 4.14. Задание разреженных списков. Продолжение

Разреженные массивы очень удобно и наглядно представлять графически. Для этого к разреженному массиву следует применить функцию ArrayPlot. В примере In[2] на рис. 4.15 мы графически представили небольшой квадратный массив размерностью 5x5, главная диагональ которого заполнена наибольшим в массиве числом 3, диагонали выше и ниже на одну ячейку заполнены числом 2, выше и ниже на две ячейки — числом 1, все остальные ячейки заполнены числом 0. Заметим, что чем меньше значение числа в ячейке, тем по умолчанию светлее тон, заполняющий её в графическом представлении в Out[2]. Можно также самостоятельно выбирать цвета, которые будут соответствовать заданным числам. Делается это во втором необязательном аргументе при помощи опции ColorRules. В примере In[3] мы обозначили 3 красным цветом, 2 — синим, 1 — зелёным, а 0 оставили по умолчанию белым. Помимо задания цветов вручную можно воспользоваться готовыми цветовыми схемами, с которыми мы познакомимся в лекции, посвящённой работе с графикой. Цветовые схемы задаются опцией ColorFunction. В примере In[4] мы использовали опцию в виде ColorFunction->{"Rainbow"}, задав этим радужную цветовую схему.

увеличить изображение
Рис. 4.15. Наглядное представление разреженных массивов графическими средствами

К настоящему моменту мы познакомились с принципами построения разреженных массивов, научились их задавать, наглядно представлять их на экране, раскрашивая в разные цвета. Но нераскрытым до сих пор остаётся вопрос: для чего же нужно использовать разреженные массивы?

В третьей лекции сего курса мы уже познакомились со средствами задания и обработки набора числовых данных — списками. Зачем же нужно ещё одно средство, да ещё и не самое простое для понимания? Для ответа на этот вопрос воспользуемся красивым примером, который приводит в П. Веллин и др. в книге [14, с. 249–250].

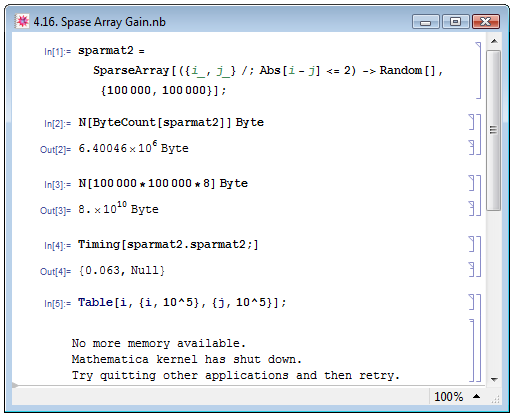
Зададим в In[1] на рис. 4.16 разреженный массив размерностью 100000x100000, состоящий из случайных чисел на главной диагонали, а также на диагоналях на одну и две строчки выше и ниже; остальные ячейки имеют значение 0. В примере In[2] при помощи функции ByteCount определим объём компьютерной памяти, который занимает массив. В нашем случае он оказывается порядка 6 мегабайт. Если мы захотим задать обычный плотный массив такой же размерности известными по лекции 3 способами, где память расходуется на все элементы, включая нулевые, то путём несложных вычислений (пример In[3]) получим, что требуемый для его хранения объём компьютерной памяти окажется порядка 80 Гбайт. При попытке задать массив при помощи известной нам функции Table Mathematica выдаёт сообщение о нехватке памяти и даже останавливает ядро, поэтому для сохранения однозначности идентификации входных и выходных данных приведём этот пример последним — In[5] на рис. 4.16.

В примере In[4] на рис. 4.16 при помощи функции Timing[oper;], возвращающей время в секундах, затраченное на выполнение математической операции oper, определим время, которое на данной машине затрачивает Mathematica на нахождение скалярного квадрата заданного разреженного массива. Оказывается, что на компьютере автора курса на это действие затрачивается даже меньше секунды.

Подробней о разреженных массивах см. книгу П. Веллина и др. [14, с. 247–250].

Рис. 4.16. Преимущества использования разреженных массивов