Работа с числами

4.2. Системы счисления

По-умолчанию Mathematica работает с числами в десятичной системе счисления (СС), однако, она позволяет переходить и к другим СС при помощи функции BaseForm[dnum,base], где dnum — число в десятичной СС, base — основание СС (пример In[1] на рис. 4.5). Обратная операция перевода числа bnum из системы с основанием base в десятичную осуществляется при помощи операции base^^bnum (пример In[2]).

В другую СС могут быть переведены не только целые числа, но также и числа остальных типов, при этом дробная часть от целой также отделяется точкой. В примере In[3] мы представляем первые 7 цифр экспоненты в двоичной СС.

Для обозначения цифр в СС с основанием больше, чем 10, используются буквы латинского алфавита. Рисунок 4.5 содержит пример In[4] представления первых 30 чисел в СС с основанием 16.

Mathematica позволяет создавать списки, содержащие в качестве элементов цифры некоторого числа. В десятичной СС это делается при помощи функции IntegerDigit[inum] для целого числа inum и при помощи функции RealDigit[rnum] для вещественного числа rnum. При этом во втором случае в качестве результата генерируется вложенный список, содержащий два элемента: первый элемент представляет собой внутренний список с цифрами числа rnum, а второй указывает, после элемента с каким номером ставится точка, отделяющая дробную часть (примеры In[5] и In[6] на рис. 4.5). Для получения списка цифр десятичного числа в СС с иным основанием base в описанные выше функции следует добавить base в качестве второго аргумента (пример In[7]).

В качестве основания СС может выступать любое целое число от 2 до 36. В примере In[8] на рис. 4.5 мы попытались задать основание СС 37: Mathematica не сумела вычислить выражение и выдала соответствующее сообщение.

Подробней о работе с различными СС см. книгу П. Веллина и др. [14, с. 227–228].

увеличить изображение
Рис. 4.5. Работа с числами в разных системах счисления

4.3. Случайные числа

При работе в области математической статистики нередко возникает необходимость прибегать к случайным распределениям чисел. В Mathematica имеется встроенная функция Random, которая в различных своих формах позволяет генерировать случайные числа в диапазоне и количестве таком, которые требуются пользователю.

Подробней о случайных числах в Mathematica см. книгу П. Веллина и др. [14, с. 229–231].

Выражение Random[] безо всяких аргументов генерирует действительное случайное число из диапазона от 0 до 1 (пример In[1] на рис. 4.6). Функция Random[Integer] случайным образом возвращает числа 0 или 1 (пример In[2]).

Функция Random может иметь три необязательных аргумента: первый задаёт тип генерируемого числа, второй — диапазон, из которого следует выбрать число. Если первый аргумент имеет значение Real, третий аргумент задаёт число цифр, используемых для представления вещественного числа. При помощи Random можно генерировать числа только трёх типов: целые (Integer), вещественные (Real) и комплексные (Complex).

В примере In[3] на рис. 4.6 мы генерируем целое случайное число из диапазона от 0 до 50.

С выражением Random[type,int] можно работать так же, как и с обычными числами, то есть, совершать с ним математические действия, использовать его в качестве аргументов функций, создавать списки и т.д. Единственное отличие при этом будет состоять в том, что при каждом новом вычислении результат будет отличаться от результата предыдущего вычисления того же самого выражения (ср. примеры In[4] и In[5] на рис. 4.6).

Рис. 4.6. Случайные числа в Mathematica

4.4. Разрядность и точность

4.4.1. Общие сведения о разрядности и точности

В Mathematica все числа, содержащие разделительную точку, рассматриваются как приближённые. При расчётах пользователь самостоятельно может в явном виде задавать приближение числа, оборвав его запись на каком-то знаке (например, записывая число 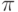с точностью до третьего знака после запятой, 3.152), либо воспользоваться автоматическим приближением при помощи функции N.

При работе с вещественными числами важными являются функции Precision и Accuracy, возвращающие разрядность и точность этих чисел. Определение этих двух понятий позаимствуем в работе Е. М. Воробьёва [1, с. 65]: "Разрядность есть число десятичных цифр, используемых "Математикой" в представлении вещественных чисел при вычислениях, в то время как точность есть число десятичных цифр, используемых для представления дробной части вещественных чисел".

При вычислениях Mathematica для вещественных чисел задаёт либо машинную (по умолчанию), либо неопределенную (произвольную) разрядность. Чтобы узнать машинную разрядность компьютера, необходимо воспользоваться выражением $MachinePrecision либо вывести численное значение константы MachinePrecision. На разных компьютерах это выражение принимает различные значения, но чаще всего его значение близко к 16. В примере In[1] на рис. 4.7 продемонстрировано, что машинная разрядность на компьютере автора курса составляет 15.9546.

Значения функций Precision и Accuracy для целых и рациональных чисел равны бесконечности, или выражению Infinity, выводимому программой в виде значка 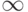(Е. М. Воробьёв [1, с. 66]) — пример In[2] на рис. 4.7. Таким образом, результат вычислений, в которых фигурируют только целые и рациональные числа, является точным. Среди функций, приводящих к точному результату при точных аргументах, функции сложения, вычитания, умножения, деления, извлечения квадратного корня, логарифма, тригонометрические функции и др. — см. примеры In[3].

Если при записи числа вводится количество цифр вещественного числа, меньшее, чем машинная точность, то считается, что его разрядность равна $MachinePrecision, если же количество введенных цифр вещественного числа превышает $MachinePrecision, то его разрядность равна количеству введенных цифр (примеры In[4] и In[5] на рис. 4.7, соответственно). Mathematica позволяет самостоятельно задавать точность и разрядность при помощи значков " ' " и " '' ", соответственно (примеры In[6] и In[7]).

Рис. 4.7. Разрядность и точность представления вещественных чисел в Mathematica