Работа с графикой: визуализация функций двух переменных
7.6. Анимация и интерактивный контроль построения изображения
Графические возможности Mathematica настолько широки, что позволяют создавать не только статические изображения, но и анимированную графику. Принцип создания анимации следующий: генерируется последовательность изображений (кадров), которые отличаются друг от друга значениями некоторого параметра, затем полученные кадры последовательно воспроизводятся.
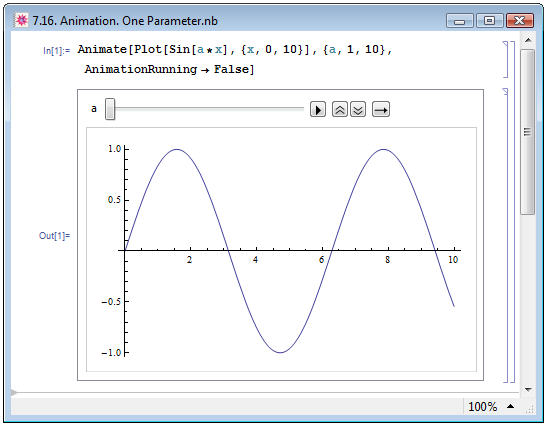
Функция программы, которая позволяет создавать анимацию — Animate. Заданная в виде Animate[plot,{u,umin,umax}] функция анимирует изображение plot в зависимости от параметра u, непрерывно меняющегося в пределах от umin до umax. Изображение plot может быть построено при помощи уже известных нам двумерных и трёхмерных графических функций. Пример создания анимации приведён на рис. 7.16: в Out[1] мы получили окно, включающее в себя изображение, полученное при помощи функции Plot, а также панель управления воспроизведением. На панели воспроизведения (слева направо) имеется ползунок, показывающий значение параметра u, при котором в данный момент построен рисунок (ползунок можно также двигать самостоятельно при помощи мышки), кнопка Play/Pause для запуска и остановки воспроизведения, кнопки увеличения и уменьшения скорости воспроизведения и кнопка изменения направления воспроизведения.
При задании функции в виде Animate[plot,{u,umin,umax,d}] параметр u меняется дискретно с промежутком d между соседними значениями. Параметр u может принимать значения, заданные пользователем самостоятельно. Для этого второй аргумент функции задаётся в виде вложенного списка {u,{u1,u2,...}}.
Меняться может сразу несколько параметров. В этом случае функция задаётся в виде Animate[plot,{u,...},{v,...},...].
Безусловно, у функции Animate имеются дополнительные опции, меняющие особенности динамического изображения.
Если задать функцию без дополнительных опций, то сразу же после осуществления вычисления анимация начинает воспроизводиться. Для того чтобы сразу после вычисления изображение оставалось статичным, а движение начиналось лишь после нажатия пользователем на кнопку Play, требуется задать опцию AnimationRunning->False.
Опция AnimationDirection задаёт направление изменения параметра u, от которого строится анимированная зависимость. По умолчанию она задана в виде AnimationDirection->Forward, и параметр u меняется от umin до umax. По достижении u значения umax анимация начинается сначала. Если задать опцию в виде AnimationDirection->Backward, u будет меняться от umax до umin. При присвоении опции значения ForwardBackward сначала u меняется от umin до umax, а по достижении значения umax — в обратную сторону, от umax до umin.
Относительная скорость анимации v определяется задающейся в следующем виде опцией AnimationRate->v. По умолчанию значение v равно 1.
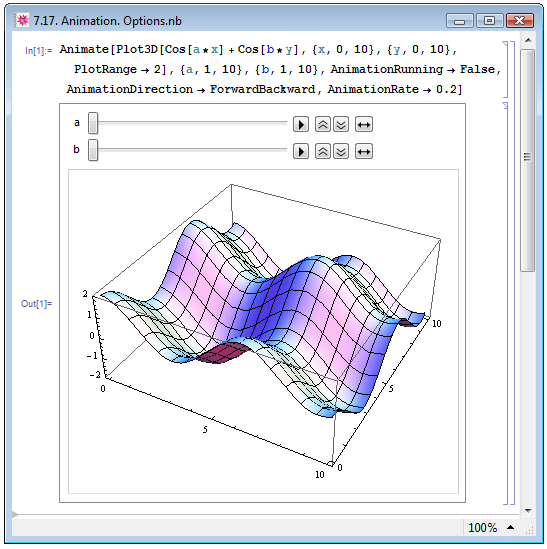
На рис. 7.17 мы создали анимацию функции ![Cos[a*x]+Cos[b*y]](/sites/default/files/tex_cache/ff974b7c3ba877dc5578bd8a2436f192.png) двух переменных x и y с изменяющимися параметрами a и b. При этом мы отключили автоматический старт анимации, AnimationRunning->False, уменьшили скорость воспроизведения анимации, AnimationRate->0.2, а также вынудили параметры a и b сначала изменяться от меньшего значения к большему, а затем в обратную сторону, AnimationDirection->ForwardBackward.
двух переменных x и y с изменяющимися параметрами a и b. При этом мы отключили автоматический старт анимации, AnimationRunning->False, уменьшили скорость воспроизведения анимации, AnimationRate->0.2, а также вынудили параметры a и b сначала изменяться от меньшего значения к большему, а затем в обратную сторону, AnimationDirection->ForwardBackward.
Подробней о функции Animate и её опциях см. книгу В. П. Дьяконова [2, с. 461–464].
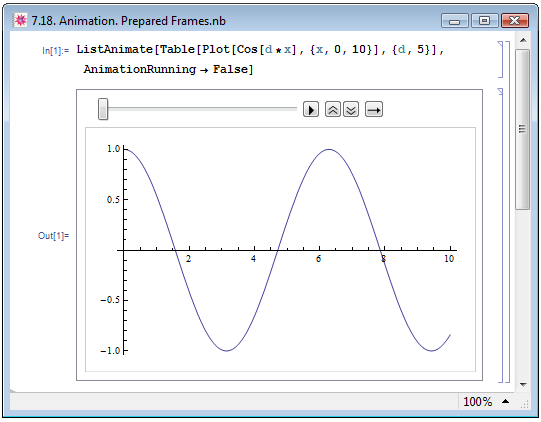
Если изображения, которые могут стать кадрами анимационного ролика, созданы заранее (например, оформлены в виде списка), то совместить их в одном ролике позволит функция ListAnimate. На рис. 7.18. мы объединили в ролике пять графиков функции ![Cos[d*x]](/sites/default/files/tex_cache/65457e039fea287900b6d7b7602dc505.png) при разных значениях d, в результате получили анимацию, последовательно воспроизводящую пять кадров.
при разных значениях d, в результате получили анимацию, последовательно воспроизводящую пять кадров.
Более широкими возможностями по сравнению с Animate обладает функция Manipulate. Применённая к некоторому выражению expr, зависящему от параметра u, функция Manipulate[expr,{u,umin,umax}] вычисляет значение выражения expr при установленном значении u. Значение u можно менять в ячейке Out[...], перетаскивая ползунок, либо вводя требуемое число в специальное поле в панели воспроизведения, появляющееся сразу после начала воспроизведения непосредственно под ползунком. Кроме того, можно наблюдать за изменением значения выражения expr, запустив автоматическое изменение параметра u в пределах от umin до umax при помощи Play.
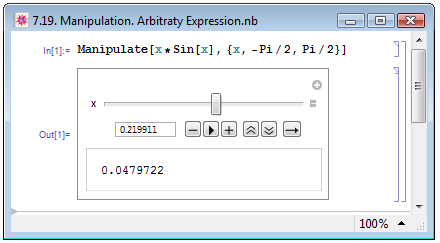
На рис. 7.19 мы привели в качестве примера вычисление значения функции x*Sin[x] при интерактивно задаваемом x.
Аргументы функции Manipulate задаются тем же способом, что и аргументы Animate: параметр может принимать непрерывные и дискретные значения, можно одновременно задавать несколько параметров. Кроме того, функция может быть задана в виде Manipulate[expr,{{u,uinit},umin,umax}]: тогда сразу после вычисления u принимает значение uinit, а не umin.
В качестве первого expr функции Manipulate может выступать функция построения изображения: именно поэтому мы рассматриваем эту функцию именно в данной лекции. В этом случае Manipulate будет представлять собой расширенную версию функции Animate, поскольку, обладая всеми её возможностями, функция Manipulate позволяет ещё и вручную задавать значения параметра, а также визуализирует его текущее значение.
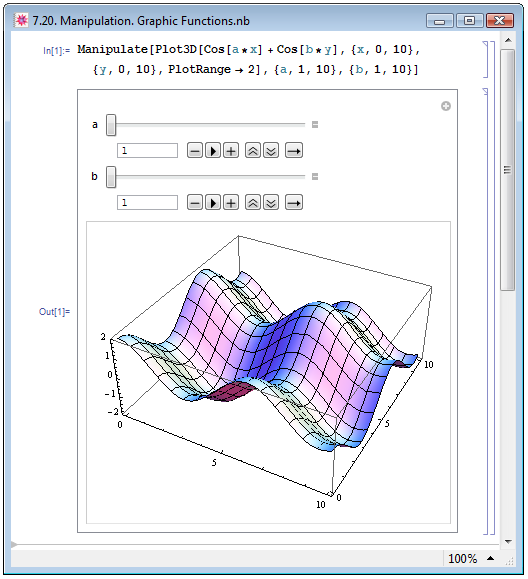
На рисунке 7.20 мы применили Manipulate к функции построения той же зависимости, что и на рис. 7.17. Как мы видим, теперь в Out[1] у нас появились дополнительные инструменты для отображения и задания значений параметров функции a и b.
Подробней о функции Manipulate и её опциях см. книгу В. П. Дьяконова [2, с. 512–513].
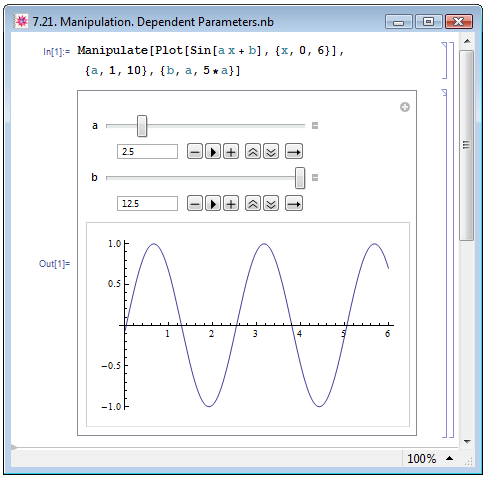
Если задаётся сразу несколько параметров манипуляции, то значения одного параметра могут зависеть от значений другого. Так на рис. 7.21 мы строим функцию Sin[a*x+b], имеющую два параметра — a и b. При этом границы изменения параметра b зависят от значения параметра а: параметр b может принимать значения от a до 5*а. В Out[1] на рис. 7.21 мы задали значение a=2.5 и выставили максимальное значение b, которое при данном a оказалось равно 12.5.
Краткие итоги
В данной лекции мы значительно расширили наши знания в области визуализации математических зависимостей средствами встроенной графики Mathematica. В частности, мы познакомились с основными графическими функциями Mathematica для визуализации явных и параметрических зависимостей от двух и трёх переменных, научились изменять внешний вид рисунков при помощи необязательных аргументов графических функций — опций. Мы познакомились с трёхмерными графическими примитивами, правилами их задания и применения. Мы также научились визуализировать динамические изображения путём создания анимированных изображений.
Вопросы
- Какой символ содержится в заголовке всех функций Mathematica, предназначенных для работы с трёхмерной графикой?
- Назовите функции Mathematica, предназначенные для визуализации непрерывных и дискретных математических зависимостей. Какие аргументы они содержат?
- В каких случаях функция ParametricPlot3D строит поверхность, а в каких — кривую в трёхмерном пространстве?
- Назовите опции двумерных графических функций, которые также используются при работе с трёхмерной графикой.
- Для каких целей используются следующие опции?
- Boxed;
- BoxRatios;
- ColorFunction;
- ViewPoint;
- Mesh;
- MeshStyle.
- Какие значения заданы по умолчанию опциям Boxed, ViewPoint?
- Какие функции Mathematica используются для визуализации зависимостей трёх переменных средствами двухмерной графики? Каким образом в отсутствии третьей пространственной координаты передаётся значение функции при заданных значениях переменных?
- К каким функциям применяются опции Contours, ContourStyle, ContourShading, PlotPoints? Какие задачи они выполняются?
- Для каких целей используется функция ContourPlot3D? Каков формат обращения ней?
- Что понимают под графическими примитивами?
- Назовите функции построения следующих графических примитивов с соответствующими аргументами: точка, линия, прямоугольник, многоугольник, дуга, диск, текст, параллелепипед, сфера, цилиндр, конус, труба. Какие из указанных примитивов используются также в двухмерной графике?
- В чём заключаются различия между примитивами "труба" и "цилиндр"?
- При задании какого примитива и с какой целью используется директива JoinForm? Какие значения она может принимать?
- Какая функция Mathematica используется для создания анимации? Какие аргументы и опции она имеет?
- Для каких целей используется функция Manipulate? В каком виде может быть задан её итератор?
Упражнения
- На одном рисунке визуализируйте зависимости
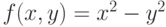 и
и 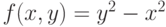 на интервалах
на интервалах  и
и  от -5 до 5, окрасьте первую поверхность красным, а вторую — зелёным. Пользуясь опцией ViewPoint, ориентируйте изображение построенных поверхностей таким образом, чтобы на экране оно выглядело как квадрат, разделённый по диагоналям на треугольники.
от -5 до 5, окрасьте первую поверхность красным, а вторую — зелёным. Пользуясь опцией ViewPoint, ориентируйте изображение построенных поверхностей таким образом, чтобы на экране оно выглядело как квадрат, разделённый по диагоналям на треугольники. - Постройте параметрическую зависимость функций
 ,
,  и
и 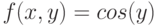 . В результате построения на рисунке должна быть изображена сфера.
. В результате построения на рисунке должна быть изображена сфера.
При помощи опции BoxRatios преобразуйте рисунок так, чтобы изображённая на нём поверхность визуально воспринималась как
- эллипсоид, вытянутый вдоль оси ординат;
- диск на плоскости, образованной осями абсцисс и аппликат.
- Постройте кривую в трёхмерном пространстве, визуализировав параметрическую зависимость функций
![f(x)=Cos[x]](/sites/default/files/tex_cache/04cd9290c7f7613178a700d6346e83e8.png) ,
, ![f(x)=Sin[x]](/sites/default/files/tex_cache/3f267ec5105e203530e36bdc52e88f79.png) и
и 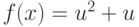 на интервале x от 0 до 30. Назовём полученное изображение "пружинкой" из-за сходства с соответствующим объектом. При помощи опции BoxRatios визуально "сожмите" "пружинку" в три раза; растяните в два раза; визуально преобразуйте звенья "пружины" из окружностей в эллипсы.
на интервале x от 0 до 30. Назовём полученное изображение "пружинкой" из-за сходства с соответствующим объектом. При помощи опции BoxRatios визуально "сожмите" "пружинку" в три раза; растяните в два раза; визуально преобразуйте звенья "пружины" из окружностей в эллипсы.
Окрасьте кривую в цвета радуги, используя соответствующую цветовую схему.
-
- создайте контурное изображение функции
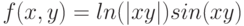 на интервалах
на интервалах  и
и  от
от 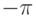 до
до 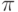 . Пользуясь опцией Contours, разбейте изображение на области, в которых
. Пользуясь опцией Contours, разбейте изображение на области, в которых 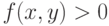 и
и 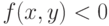 .
. - закрасьте области, соответствующие условию
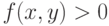 , красным цветом, а условию
, красным цветом, а условию 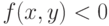 — синим.
— синим. - измените полученное в предыдущем пункте изображение, отменив закрашивание областей и оставив на рисунке только контуры.
- создайте плотностное изображение той же функции на прежних интервалах. Окрасьте изображение в градации синего. Улучшите изображение, разбив интервал изменения каждого из аргументов на 52 отрезка.
- совместите на одном рисунке изображения, полученные в пунктах (в) и (г).
- создайте контурное изображение функции
- Постройте дискретную зависимость функции
 на интервалах
на интервалах  и
и  от
от 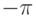 до
до 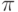 с шагом
с шагом  помощи функции ListPlot3D. Для этого предварительно при помощи функции Table создайте список, содержащий значения переменных
помощи функции ListPlot3D. Для этого предварительно при помощи функции Table создайте список, содержащий значения переменных  и
и  и соответствующие им значения функции
и соответствующие им значения функции 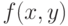 .
.
Постройте в отдельности друг от друга контурное и плотностное изображения этой же функции, затем совместите их на одном рисунке, предварительно убрав заливку на контурном изображении.
- Используя примитивы трёхмерной графики нарисуйте снеговика, робота, ракету, автомобиль, Останкинскую телебашню.
Используя только примитив "труба", нарисуйте каркас тетраэдра, куба, октаэдра.
- Средствами Mathematica создайте примитивную анимацию волн на водной поверхности. Для этого, используя тригонометрические функции синуса и косинуса, задайте периодическую функцию двух переменных
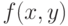 , имитирующую водную гладь. При задании введите в
, имитирующую водную гладь. При задании введите в 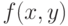 два параметра, управляющих периодом тригонометрических функций. Можно также задать параметры, управляющие амплитудой колебаний. Используйте наиболее подходящую заданию цветовую схему.
два параметра, управляющих периодом тригонометрических функций. Можно также задать параметры, управляющие амплитудой колебаний. Используйте наиболее подходящую заданию цветовую схему.
Для создания анимации воспользуйтесь функцией Animate.