Работа со списками
Цель лекции: познакомиться с одним из основных классов данных Mathematica — списками, познакомиться с принципами работы с ними
3.0. Введением
Значительная доля вычислений так или иначе связана не с отдельными выражениями, а с целыми массивами тем или иным образом сгруппированных данных. Именно поэтому для работы с такими данными в Mathematica существует целый класс данных, называемый списками. Как мы помним из предыдущей лекции, список представляет собой удобную форму структурирования данных, по строению представляет собой множество элементов, заключённых в фигурные скобки { } и разделённых запятыми: {expr1,expr2,...}. Для каждой открывающей фигурной скобки { в списке должна присутствовать закрывающая фигурная скобка }. Элементами списка могут быть любые выражения: числа, символы, строки, функции, графические изображения, а также другие списки. Для работы со списками в Mathematica имеется широчайший набор инструментов: можно различными способами создавать списки, преобразовывать их, а также извлекать информацию из уже имеющихся списков. Для знакомства с указанными возможностями воспользуемся логикой изложения материала в работе П. Веллина и др. [14].
3.1. Создание списков
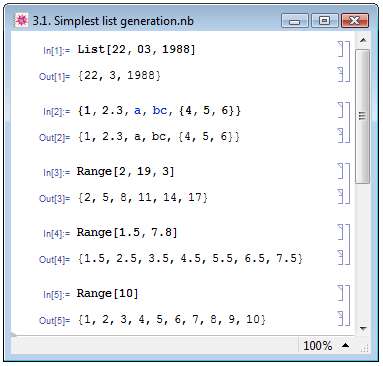
В Mathematica список есть выражение, имеющее заголовок List, поэтому наиболее естественный для Mathematica способ задания списка — в виде List[element1,element2,...], где element1,element2,... — элементы списка (пример In[1] на рис. 3.1). С более простым и наглядным для пользователя способом задания списка мы уже познакомились в предыдущей лекции: он заключается в том, чтобы ввести через запятую элементы списка и обособить их фигурными скобками (пример In[2]).
Если список включает в себя только числа одного из трёх типов: целые, рациональные или вещественные — и элементы списка подчиняются какой-либо периодической закономерности, то задать список можно, воспользовавшись функцией Range[imin,imax,di]. В результате генерируется список от наименьшего значения imin с приращением (разностью между соседними элементами) di до значения меньшего или равного imax.
В примере In[3] на рис. 3.1 мы создаём список целых чисел, начиная от числа 2. Последующие элементы получаются добавлением к текущему элементу числа 3. Наибольшее значение элемента списка не будет превышать числа 19.
Если приращение di равняется единице, можно воспользоваться упрощённой версией функции — Range[imin,imax]. Так в примере In[4] на рис. 3.1 мы задаём список вещественных чисел, начиняя от числа 1.5. Поскольку приращение не задано, последующие элементы генерируются прибавлением к предыдущим элементам единицы. Наибольшее значение элемента списка не будет превышать числа 8.
Существует ещё более простая версия функции — Range[imax], которая задаёт ряд натуральных чисел от 1 до значения меньшего или равного imax: это может понадобиться, например, в случае, когда требуется задать нумерацию. Так в примере In[5] на рис. 3.1 мы генерируем ряд натуральных чисел от 1 до 10.
Подробней о функции Range см. книги Е. М. Воробьёва [1, с. 101, 161] и П. Веллина и др. [14, с. 55–56].
Mathematica позволяет задавать и более сложно устроенные списки числовых данных. Для этого используется функция Table. В наиболее полной своей форме функция выглядит следующим образом: Table[expr,{i,imin,imax,di}]. Первый аргумент функции, expr, представляет собой выражение, которое вычисляется в процессе построения списка, и вычисленное значение включается в список как один из его элементов. Второй аргумент функции, {i,imin,imax,di}, называется итератором (iterator). В случае Mathematica итератор можно рассматривать как объект, указывающий на расположенные определённым образом элементы в наборе данных. Итератор представляет собой перечень параметров, определяющих в конечном итоге число элементов списка. Параметры могут также входить в выражение expr в качестве констант или переменных. Параметр imin принимает численные значения и определяет первое значение переменного параметра i, приращение di — величина, использующаяся для задания последующих элементов списка, число imax определяет наибольшее возможное значение i: если при возрастании значения i с интервалом di получается величина, превышающая imax, то построение списка заканчивается, а полученное значение при этом не используется.
В примере In[1] на рис. 3.2. при помощи функции Table мы задаём список элементов, удовлетворяющих выражению 2*k, причём k меняется от 1.1 до 15 с интервалом 2.
При помощи функции Table[i,{i,imin,imax,di}] можно продублировать уже известную нам функцию Range[imin,imax,di] (пример In[2] на рис. 3.2: ср. списки, полученные в Out[2]). И точно так же функцию Table можно записывать в упрощённом виде: Table[expr,{i,imin,imax}] — когда приращение равно единице, Table[expr,{i,imax}] — когда равны единице приращение di и первое значение переменного параметра i (соответствующие примеры In[4] и In[5]).
Если выражение expr не зависит от переменного параметра, то функцию можно записать как Table[expr,{imax}]: она генерирует ряд, содержащий число элементов, равное целой части выражения imax, причём каждый элемент содержит выражение expr. Однако здесь с подачи Е. М. Воробьёва [1, с. 101–102] необходимо сделать уточнение. Дело в том, что одно и то же исходное выражение expr в ряде случаев при вычислении может давать различные результаты. Для понимания этого неожиданного заявления рассмотрим функцию Random, часто используемую в математическом моделировании. Выражение Random[] в качестве результата вычисления возвращает однородно распределенную псевдослучайную вещественную величину, заключенную в интервале от 0 до 1. Поэтому выражения Table[Random[],{imax}] генерирует ряд случайных чисел со значением от 0 до 1, состоящий из imax числа элементов — см. пример In[6] на рис. 3.2.
Скажем ещё несколько слов о функции Random. Выражение Random[type,{imin,imax}] задаёт случайное число, принадлежащее интервалу {imin,imax} и относящееся к типу type, где type принимает значения типов чисел, Integer, Real или Complex. В случае типа Real третий аргумент функции Random может задавать число цифр, используемых при задании вещественного числа.
Подробней о функции Random см. книгу Е. М. Воробьёва [1, с. 101–102].
В примере In[7] на рис. 3.2. мы генерируем целое число, принадлежащее промежутку от 5 до 101, а в In[8] — вещественное число из промежутка от 3.5 до 7.1, причём представляем его с точностью до пятнадцати значащих цифр.
Функция Table также позволяет генерировать вложенные списки, то есть, списки, элементами которых являются другие списки. Списки, являющиеся элементами вложенного списка, называются внутренними. Это делается путём добавления в функцию ещё одного итератора — пример In[1] на рис. 3.3. Когда функция содержит больше одного итератора, порядок итераторов оказывается существенным, поскольку значения внешнего итератора различны для каждого значения внутреннего итератора. В нашем примере In[1] для каждого значения j (внутренний итератор) параметр i (внешний итератор) изменяется от 1 до 3, при этом создаётся список из четырех элементов, каждый из которых содержит ещё по 3 элемента. Если мы поменяем в выражении In[1] порядок итераторов, то получим список из трех элементов, каждый из которых содержит по четыре элемента — пример In[2].
Подробней о функции Table см. книги Е. М. Воробьёва [1, с. 101–103] и П. Веллина и др. [14, с. 56–58].