Работа со списками
3.3. Извлечение элементов списка
При помощи функции Part[list,n] можно извлечь из списка list элемент, зная его позицию n в списке. Эту функцию также можно задать в сокращённом виде, используя двойные скобки: list[[n]]. Чтобы обратиться сразу к нескольким элементам списка, следует задать функцию в виде Part[list,{n1,n2,...}] или list[[{n1,n2,...}]], где n1,n2,... — номера элементов, которые требуется извлечь.
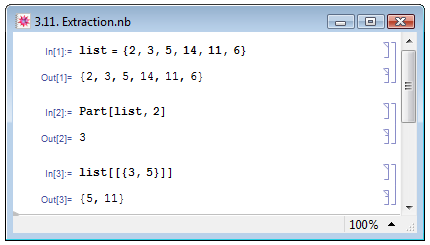
В примере In[1] на рис. 3.11 мы задали одноуровневый список list, в In[2] при помощи полной формы функции Part мы извлекли второй элемент списка list, а в In[3], — используя сокращённую форму, третий и пятый элементы.
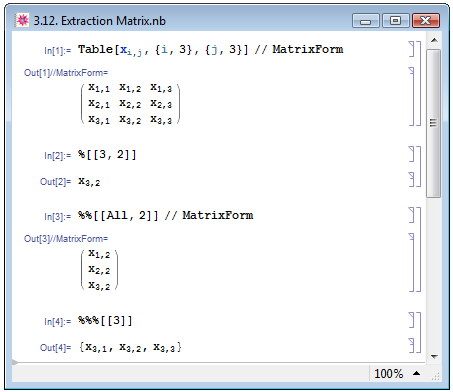
Для того чтобы извлечь элемент из вложенного списка, необходимо указать и номер подсписка, в котором находится необходимый элемент, и номер элемента в этом подсписке. На рис. 3.12 приведён пример извлечения элементов матрицы 3х3. В примере In[2] мы извлекаем элемент с номером 2 из третьего подсписка. В примере In[3] мы полностью извлекаем второй столбец матрицы, заменив номер подсписка на выражение All, а в примере In[4] — третью строку, которая также является третьим подсписком исходного списка, причём мы можем либо заменить номер элемента на All, либо вовсе опустить этот параметр.
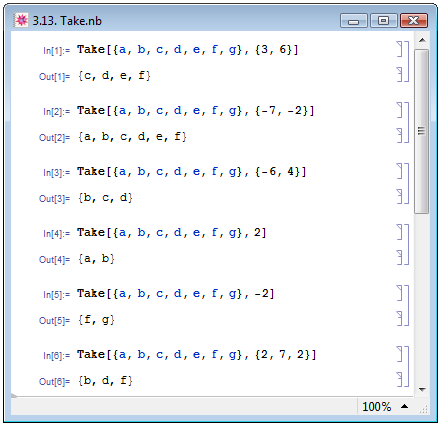
Для обращения к элементам списка в Mathematica имеется ещё одна функция — с заголовком Take. В своей простейшей форме Take[list,{b1,b2}] она возвращает фрагмент списка list, содержащий элементы с номерами от b1 до b2, причём если b1, b2 принимают положительные значения, то номер элемента отсчитывается от первого (пример In[1] на рис. 3.13), а если отрицательные — от последнего (пример In[2]). При этом b1 и b2 могут принимать положительные и отрицательные значения независимо друг от друга (пример In[3]).
Если функция задаётся в виде Take[list,b], при положительном b возвращается фрагмент списка, начиная от элемента с номером 1 до элемента с номером b, а при отрицательном b — от элемента с номером абсолютного значения b с конца списка до последнего элемента в списке (примеры In[4] и In[5] на рис. 3.13).
В наиболее полной форме Take[list,{b1,b2,di}] функция из списка list выбирает каждый di-й элемент, начиная с элемента под номером b1 и заканчивая элементом с номером, не большим, чем b2 (пример In[6] на рис. 3.13).
Подробней об управлении содержанием списка см. книги Е. М. Воробьёва [1, с. 105–106] и П. Веллина и др. [14, с. 62–63].
3.4. Преобразование списков
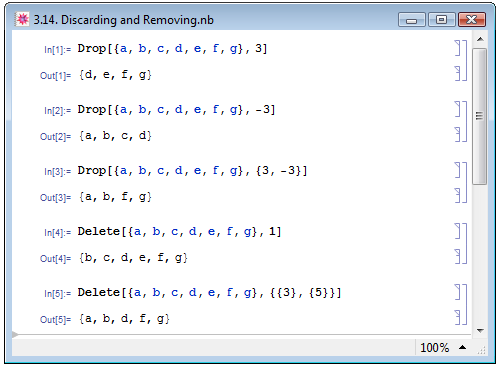
Mathematica позволяет отбрасывать фрагменты списка при помощи функции Drop[list,bound], где bound задаёт фрагмент списка list, который необходимо отбросить. Правила задания функции Drop такие же, как и для Take. Примеры отбрасывания элементов в начале, конце и в произвольном месте списка представлены на рис. 3.14 как In[1], In[2] и In[3], соответственно.
Помимо отбрасывания целых фрагментов Mathematica позволяет селективно удалять элементы списка с определёнными номерами при помощи функции Delete[list,{{n1},{n2},...}], где n1,n2,...— номера элементов списка list, которые необходимо удалить — примеры In[4] и In[5] на рис. 3.14.
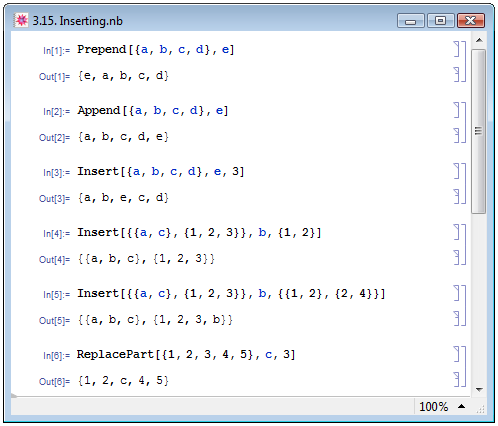
Mathematica позволяет добавлять в списки новые элементы. Для добавления элементов в начало и конец списка имеются соответствующие функции: Prepend[list,n] и Append[list,elem] (см. примеры In[1] и In[2] на рис. 3.15).
Функция Insert[list,elem,n] помещает выражение elem на позицию n в списке list, причём число n может принимать как положительные, так и отрицательные значения (пример In[3] на рис. 3.15).
Как мы уже отмечали, элементами списка могут быть любые выражения, в том числе и списки. Новый элемент elem можно вставить в любой внутренний список в списке list или внутрь любого элемента списка, если этот элемент не является атомарным выражением. В примере In[4] на рис. 3.15 указание позиции в виде {1,2} означает, что новый элемент нужно вставить в первый элемент списка на вторую позицию. Один и тот же элемент можно вставить на несколько позиций — см. пример In[5].
Mathematica позволяет осуществлять суперпозицию описанных выше функций удаления и добавления элементов в список — заменять один элемент другим. Делается это при помощи функции ReplaceRart[list,elem,n], которая заменяет элемент списка list под номером n элементом elem — см. пример In[6] на рис. 3.15.
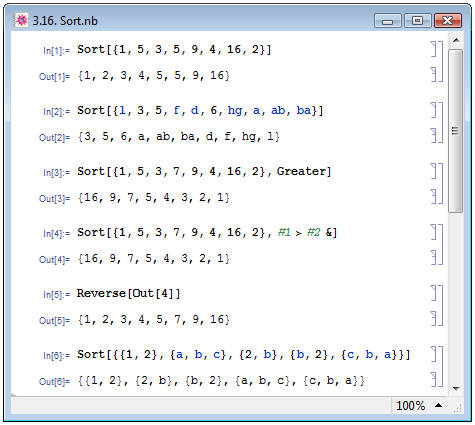
Элементы списка можно отсортировать в каноническом порядке, принятом в Mathematica, при помощи функции Sort[list]. Автоматически Mathematica производит сортировку списков следующим образом: целые, рациональные и вещественные числа сортируются по возрастанию значения, комплексные — по возрастанию значения действительной части, а при равных её значениях — по абсолютной величине мнимой части; символы и строки сортируются по алфавиту, степени и произведения сортируются так же, как и члены в полиноме, по возрастанию степени; в списках, содержащих смешанные данные (числа, символы строки), сначала сортируются численные данные, а за ними — "буквенные", т.е., символы и строки. Примеры In[1] и In[2] канонической сортировки см. на рис. 3.16.
Функция Sort[list,cond] позволяет отсортировать список в порядке, заданном пользователем, при чём cond — условие, по которому будет происходить сортировка. Например, если эту функцию мы применим к списку чисел list с условием cond равным Greater, то список будет сортирован по убыванию. Условие Greater можно записать в следующем виде: #1>#2&. Подобная конструкция, как мы уже знаем, является анонимной функцией. Пример сортировки по заданному пользователем критерию In[3] и In[4] см. на рис. 3.16. Изменить направление сортировки можно также при помощи функции Reverse[list] — пример In[5].
Если мы попробуем автоматически отсортировать вложенный список, то упорядочение будет вестись по первому элементу каждого внутреннего списка, а списки с большим числом элементов будут располагаться после списков с меньшим числом — см. пример In[6] на рис. 3.16.
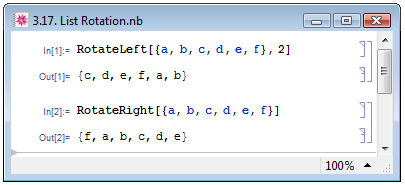
В Mathematica имеются функции, позволяющие циклически переставлять элементы списков справа налево RotateLeft[list,n] и слева направо RotateRight[list,n], где n определяет число позиций, на которое следует сдвинуть элементы списка list в ту или иную сторону. Если параметр n опущен, то перестановка осуществляется на одну позицию. Примеры использования функций перемещения см. на рис. 3.17.
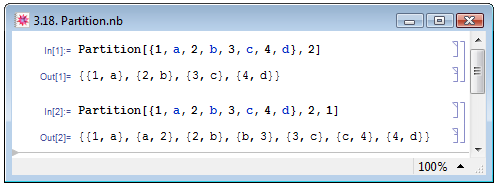
Mathematica позволяет из линейных списков создавать вложенные списки. При помощи функции Partition[list,n] линейный список list преобразуется во вложенный список, причём внутренние списки не перекрываются и содержат по n элементов (см. пример In[1] на рис. 3.18). Для создания перекрывающихся списков используется функция в виде Partition[list,n,w], по выполнении которой генерируется вложенный список, содержащий n внутренних списков, причём w последних элементов предыдущего списка становятся w первыми элементами последующего списка (пример In[2]).
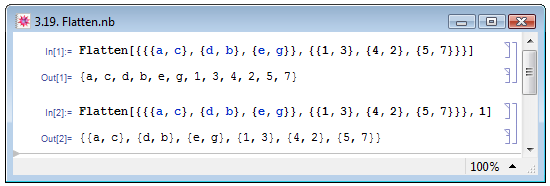
Возможна в программе и обратная операция — объединение элементов вложенного списка в один линейный список. Так функция Flatten[list], где list — вложенный список, убирает заголовок List у всех внутренних списков и превращает list в одноуровневый список. Заданная в более полном виде функция Flatten[list,n] убирает заголовок List только до уровня n включительно, т.е., список, полученный в результате выполнения этой функции, может быть и не одноуровневым. Соответствующие примеры см. на рис. 3.19.
Обратимся теперь к функциям, которые рассматривают список скорее как множество, а не как упорядоченную структуру.
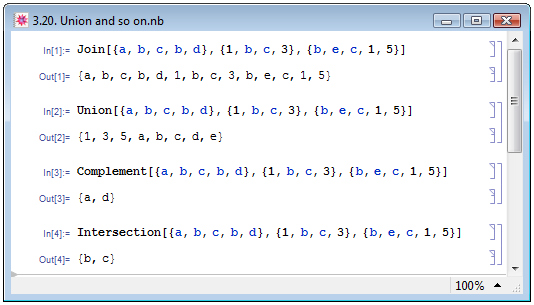
Простейшей для понимания из них является функция Join[list1,list2,...], осуществляющая сцепление (конкатенацию) списков независимо от содержащихся в них элементов (пример In[1] на рис. 3.20). Вообще говоря, в списке могут содержаться совпадающие элементы. Применение к нему функции Union[list] приводит к удалению повторений элементов и к сортировке оставшихся. Если аргумент этой функции будет содержать несколько списков, то результатом будет список, состоящий из элементов этих списков, причём повторяющиеся элементы также будут удалены.
Функция Intersection[list1,list2,...] возвращает список элементов списка list, содержащихся в списках list1, list2..., а Complement[list1,list2,...] — НЕ содержащихся в списках. Повторные элементы в результирующих списках также будут удалены. Примеры работы с повторяющимися элементами списков также см. на рис. 3.20.
Подробней о преобразовании списков см. книги Е. М. Воробьёва [1, с. 103–110] и П. Веллина и др. [14, с. 63–66, 69].