Работа со списками
3.5. Использование списков в качестве аргументов функций
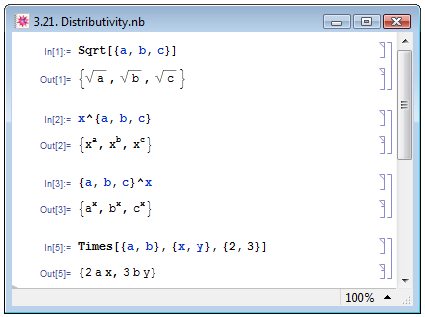
Если мы попробуем вычислить значения некоторых встроенных функций Mathematica от списков, то на выходе получим список той же размерности, что и начальный, элементы которого являются результатом применения функции к каждому элементу списка в отдельности. См. на рис. 3.21 примеры применения к списку функции извлечения квадратного корня Sqrt[list] (In[1]), а также возведения в степень x^list (In[2]) и list^x (In[3]). Эти примеры демонстрируют свойство встроенных функций, которое можно назвать дистрибутивностью относительно списков (Е. М. Воробьёв [1, с. 118]).
Применение дистрибутивных функций к спискам одинаковой длины имеет свою специфику, которую доступно описывает Е. М. Воробьёв [1, с. 120]: "...при применении дистрибутивной функции от нескольких аргументов к спискам одинаковой длины происходит следующее: сначала производится транспозиция списков, т.е. объединяются в списки элементы с одинаковыми номерами из разных списков, потом функция применяется к вновь образованным спискам так, что элементы этих списков становятся аргументами функции". Иллюстрация сказанного представлена на примере In[4] на рис. 3.21. Сначала из трёх списков, содержащих по два элемента, сформировались два списка по три элемента. Затем заголовок List полученных списков был заменён заголовком Times.
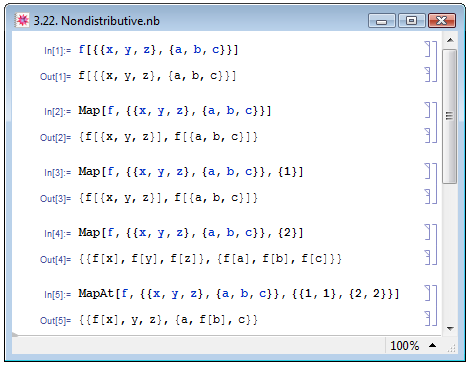
Если же к списку применить произвольную функцию f, то она, не обладая свойством дистрибутивности, даст неопределённый результат — пример In[1] на рис. 3.22. Однако заставить функцию f вести себя как дистрибутивную по отношению к списку list можно при помощи функции Map[f,list] — пример In[2] на рис. 3.22.
Если функция задана в виде Map[f,list,k], k задаёт спецификацию уровня, определяющую уровень списка list, к элементам которого будет применяться функция f — примеры In[3] и In[4] на рис. 3.22. Похожей по действию является функция MapAt[f,list,k]: она применяет заголовок f к элементам списка list в соответствии с их спецификацией — см. пример In[5].
Функция Attributes[function] позволяет узнать, является ли некоторая функция дистрибутивной относительно списков Если среди атрибутов функции function присутствует listable, то она дистрибутивна.
С функцией Map мы встретимся ещё раз, когда будем говорить о функциональном программировании в Mathematica.
Подробней об использовании списков в качестве аргументов функции см. книгу Е. М. Воробьёва [1, с. 117–123].
3.6. Работа с векторами и матрицами
Наиболее точно и ёмко векторы и матрицы в Mathematica определяет Е. М. Воробьёв [1, с. 110]: "Векторы в Mathematica трактуются как линейные, т.е. одноуровневые, списки: v={vl,v2,v3,...}; матрицы как двухуровневые: т={{mll,ml2,ml3,...},{m21,m22,m23,...}}, хотя компоненты векторов и матриц могут быть произвольными выражениями". Поскольку эти объекты играют немаловажную роль в математике и физике, разработчики Mathematica определили ряд функций, предназначенных для работы именно с ними.
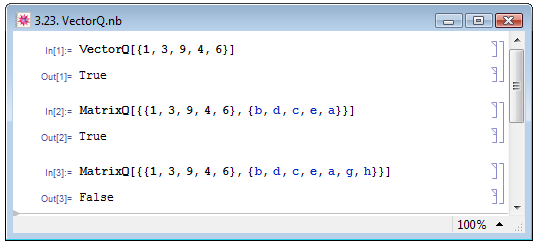
Во-первых, это функции проверки, является ли список list вектором VectorQ[list] или матрицей MatrixQ[list]. При положительном результате функции возвращают True, иначе — False (см. пример на рис. 3.23).
Если некоторое выражение m действительно является матрицей, то к нему применимы описанные ниже функции.
Определитель (детерминант) матрицы m вычисляется функцией Det[m].
Функция Tr[m] возвращает след матрицы m.
Для невырожденных квадратных матриц можно вычислить обратную матрицу при помощи функции Inverse[m].
Функция Transpose[m] проводит транспонирование матрицы m.
Функция Minors[m,k] генерирует список миноров k-го порядка матрицы m.
Для нахождения скалярного произведения векторов, произведения вектора и матрицы, произведения матриц используется функция Dot[expr1,expr2]. В упрощённом виде, в так называемой инфиксной форме (shorthand notation), эту функцию можно задать как exprl.expr2.
Векторное произведение векторов v1 и v2 находится при помощи функции Cross[v1,v2].
Для нахождения нормы вектора v используется функция Norm[v].
Собственные числа и собственные векторы матриц находятся соответственно функциями Eigenvalues[expr] и Eigenvectors[expr], а одновременно и то, и другое — функцией Eigensystem[expr]. Функция CharacteristicPolynomial[expr] дает характеристический полином матрицы.
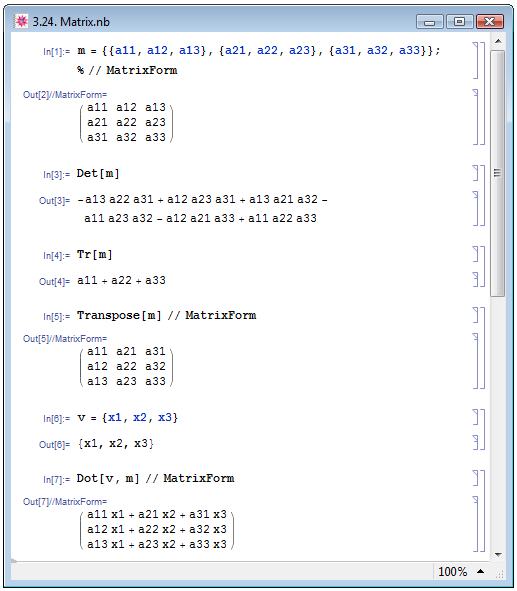
Некоторые примеры использования функций для работы с матрицами представлены на рис. 3.24.
Подробней о работе с векторами и матрицами см. книгу Е. М. Воробьёва [1, с. 110–112].