Процедурное программирование
Цель лекции: познакомиться с основами реализации процедурного стиля программирования в языке программирования Mathematica
11.0. Введение
В предыдущих лекциях мы познакомились с двумя наиболее естественным для Mathematica стилями программирования — функциональным и стилем, основанным на правилах преобразований. Однако Mathematica позволяет также программировать, используя исторически первый и традиционный стиль для большинства языков программирования (Фортран, Паскаль, С и др.) — процедурный стиль. Процедурный стиль в отличие от остальных зачастую не самым эффективным образом использует машинные ресурсы, но он более нагляден, более привычен для пользователей и именно поэтому он поддерживается Mathematica и успешно используется при решении многих задач.
В данной лекции мы рассмотрим процедурный стиль программирования, за основу взяв книги Е. М. Воробьёва [1], П. Веллина и др. [14] и С. Мангано [11].
11.1. Условные функции
11.1.1. Функция If
Условные функции позволяют задавать различный характер вычислений в зависимости от выполнения или невыполнения одного или нескольких условий. В языках программирования их принято называть условными операторами. Будем придерживаться этой традиции и мы. Более строго условный оператор или оператор ветвления определяется следующим образом: это конструкция языка программирования, обеспечивающая выполнение определённой команды (набора команд) только при условии истинности некоторого логического выражения, либо выполнение одной из нескольких команд (наборов команд) в зависимости от значения некоторого выражения.
Наиболее простым в использовании является оператор If. Как правило, он задаётся в виде If[cond,expr1,expr2]. Результат вычисления данного выражения есть выражение expr1, если при вычислении cond возвращается True, и, соответственно, выражение expr2, если вычисление cond даёт False.
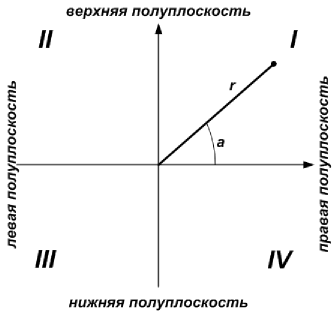
Для иллюстрации действия оператора If и других условных операторов рассмотрим следующую задачу. Пусть на плоскости задана некоторая точка, которая в полярных координатах описывается произвольным отличным от нуля радиусом r и углом a. Зная величину угла a, нам необходимо определить, какой (верхней или нижней относительно оси абсцисс) полуплоскости принадлежит эта точка. Саму ось абсцисс мы отнесём к верхней полуплоскости. Для наглядности см. рис. 11.1.
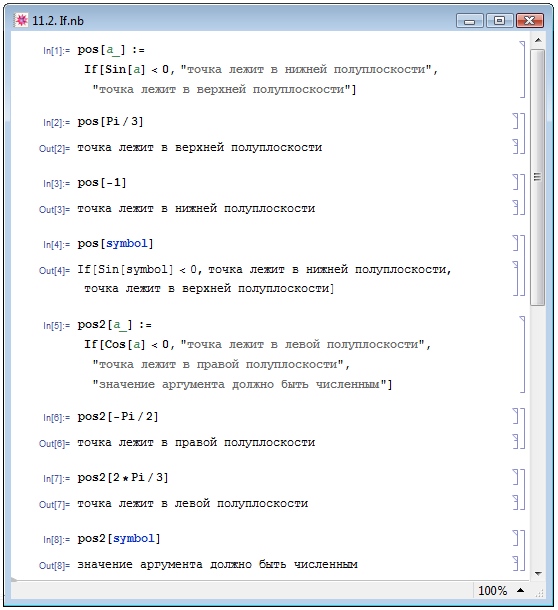
В In[1] на рис. 11.2 мы задали пользовательскую функцию pos одного аргумента a, тело которой содержит условный оператор. При обращении к этой функции с некоторым значением аргумента a в выходной ячейке печатается фраза "точка лежит в нижней полуплоскости", если синус значения аргумента a принимает отрицательные значения, и "точка лежит в верхней полуплоскости", если положительные или 0; в примерах In[2] и In[3] мы проверяем действие нашего условного оператора для значений аргумента, удовлетворяющих каждому из условий.
Если вычисление выражения cond не возвращает ни True, ни False, условный оператор остаётся невычисленным и перепечатывается в ячейку Out в исходном виде. В качестве иллюстрации в примере In[4] на рис. 11.2 мы задали в качестве аргумента нашей функции pos выражение, отличное от числа.
Для того чтобы любой результат вычисления выражения cond приводил к вычислению условного оператора, используется расширенная форма условного оператора, которая выглядит как If[cond,expr1,expr2,expr3]. В этом случае, если вычисление выражения cond не возвращает ни True, ни False, результатом вычисления условного оператора будет являться выражение expr3.
В In[5] на рис. 11.2 мы задали новую пользовательскую функцию pos2 одного аргумента a. При обращении к этой функции с некоторым значением аргумента x в выходной ячейке печатается фраза "точка лежит в левой полуплоскости", если косинус значения аргумента a принимает отрицательные значения, и "точка лежит в правой полуплоскости", если положительные или 0. Если ни первое, ни второе условие не выполняется (когда значение аргумента a не является числом), печатается фраза "значение аргумента должно быть численным". В примерах In[6], In[7] и In[8] мы обращаемся к нашей функции при значениях аргументов, инициирующих разные результаты вычисления оператора If.
В качестве аргументов expr1,expr2 и expr3 оператора If могут выступать абсолютно любые выражение Mathematica, в том числе и другие условные операторы. Таким образом, помимо задания дихотомии, выбора между двух взаимоисключающих условий, используя определённое сочетание условных операторов, можно задавать любое количество исключающих друг друга условий, выполнение которых влечёт различные результаты вычислений.
В следующем примере мы ещё более конкретизируем положение нашей точки на координатной плоскости. Мы определим её положение с точностью до квадранта и отдельно установим, если точка лежит на оси координат.
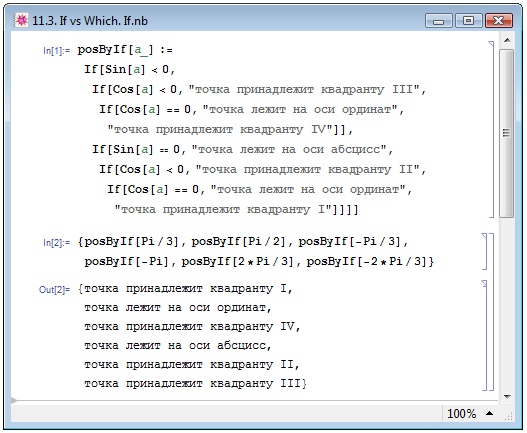
В In[1] на рис. 11.3 мы задали пользовательскую функцию posByIf от одного аргумента a. При обращении к этой функции с некоторым значением аргумента a в случае, если синус a принимает отрицательные значения, то выполняется вложенный условный оператор. Этот оператор проверяет, является ли косинус аргумента отрицательным. В случае если это так, печатается фраза "точка принадлежит квадранту III". В противном случае выполняется ещё один условный оператор, который проверяет, не принимает ли выражение Cos[a] нулевых значений: в случае, если принимает, печатается фраза "точка лежит на оси ординат", в противном случае печатается фраза "точка принадлежит квадранту IV". Если синус аргумента a не принимает отрицательных значений, выполняется иная последовательность, в которой определяется принадлежность значения аргумента a первому или второму квадрантам, либо осям абсцисс или ординат. В примере In[2] мы проверяем действие нашей функции posByIf для нескольких значений аргумента.
Подробней о функции If см. книги Е. М. Воробьёва [1, с. 167–168] и П. Веллина и др. [14, с. 131–135].